🎒 knapsack problem

• 고정된 크기의 배낭에 물건들을 담아 배낭에 담긴 물건들의 가치의 합을 최대화하는 문제

🔍 동적 계획법을 사용한 풀이

• 배낭의 크기가 7이고, 4개의 물건의 무게와 가치가 다음과 같다고 가정해보자.

• 2차원 배열을 만들고 각 행과 열에 최대 가치를 저장해 나간다.

  • 행 i 은 물건을, 열 j 은 가방의 최대 무게를 의미한다.

• 최대 가치를 저장하는 방법은 다음과 같다.

  1. 물건 i 을 가방에 넣을 수 있을 때 (물건의 무게가 가방의 크기보다 작을 때)
     • 해당 물건을 가방에 넣고 남은 크기가 없다면 해당 물건의 가치와 dp[i-1][j]에 저장된 값의 최댓값이 최대 가치
     • 해당 물건을 넣고 남은 크기가 있다면 해당 물건의 가치 + 남은 무게에 들어갈 수 있는 최대 가치
  2. 물건을 가방에 넣을 수 없을 때 (물건의 무게가 가방의 크기보다 클 때)
     • dp[i-1][j]에 저장된 값을 그대로 저장한다.

• 최종 결과는 dp[n][k]에 저장된다. (n은 물건의 개수, k는 배낭의 크기)

✏️ 표를 그려 이해해보자 !

1. 첫 번째 물건 (무게 6, 가치 13)을 담아보자.
   

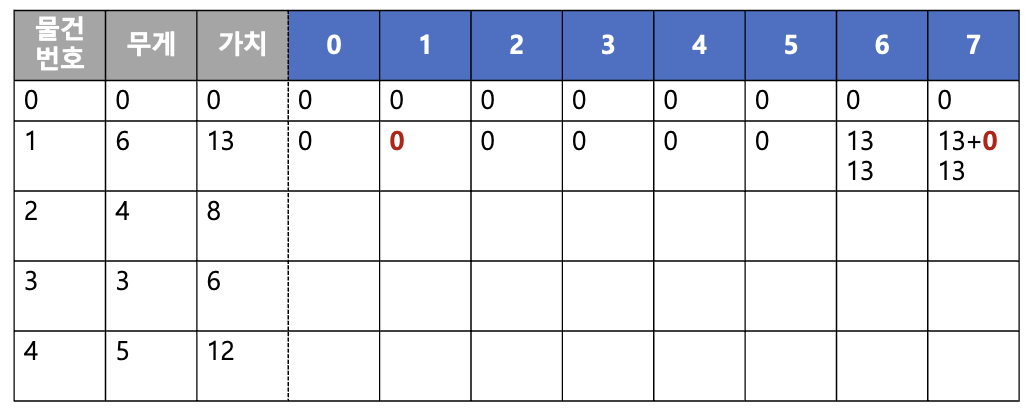
• 가방의 크기가 6이하일 때는 바로 위 인덱스 dp[0][j]에 저장된 값을 저장한다. 이 경우에는 모두 0이다.
• 가방의 크기가 6일 때 더이상의 남는 공간은 없으므로 1번 물건의 가치인 13을 저장한다.
• 가방의 크기가 7일 때 남는 공간 1이므로 13+dp[1][1] = 13+0 = 13 이 저장된다.

2. 두 번째 물건 (무게 4, 가치 8)을 담아보자.
   

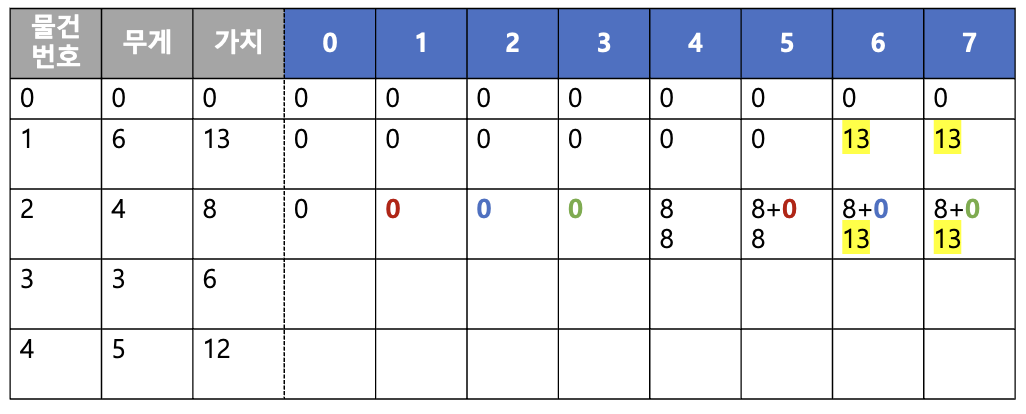
• 가방의 크기가 4이하일 때는 바로 위 인덱스 dp[1][j]에 저장된 값을 저장한다. 이 경우에는 모두 0이다.
• 가방의 크기가 4일 때는 남는 공간이 없으므로 2번 물건의 가치인 8과 dp[1][4]에 저장된 값을 비교하여 최댓값을 저장한다. 이 때는 위에 저장된 값이 0이므로 8이 저장된다.
• 가방의 크기가 5일 때는 남는 공간이 1이므로 8+dp[2][1] = 8+0 = 8 이 저장된다.
• 가방의 크기가 6, 7일 때도 남는 공간을 이용하여 8+dp[2][2] = 8+0 = 8, 8+dp[2][3] = 8+0 = 8을 계산할 수 있지만 위에 저장된 값(dp[1][j])과 비교했을때 최댓값인 13이 각각 저장된다.

3. 같은 방법으로 세번째, 네번째 물건도 담아보면
   

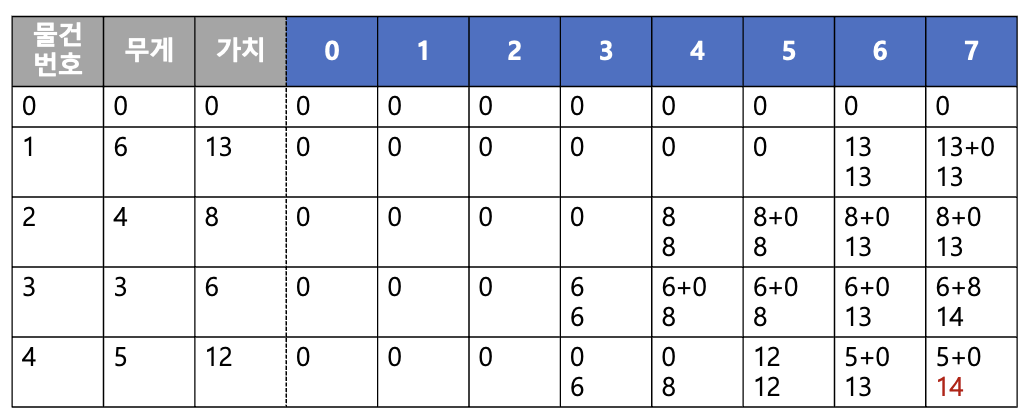
• 최종적으로 dp[n][k]에 저장된 14가 배낭이 담을 수 있는 최대 가치가 된다.

📍 코드 작성

n, k = map(int, input().split())  # 물건 개수, 배낭 크기
dp = [[0 for _ in range(k + 1)] for _ in range(n + 1)]  # 배열

item = [[0, 0]]
for i in range(1, n + 1):  # 물건의 무게, 가치 입력
    item.append(list(map(int, input().split())))

Max = 0
for i in range(1, n + 1):  # 물건 개수만큼 반복
    for j in range(1, k + 1):  # 배낭의 크기까지 반복

        weight = item[i][0]
        value = item[i][1]
        
		# 가방에 넣을 수 없으면 위의 값 그대로 가져오기
        if j < weight:
            dp[i][j] = dp[i - 1][j]  
            
        # 가방에 넣을 수 있으면
        # 위에 값 vs (현재 아이템 가치 + 그전 단계에서 구한 남은무게의 가치)
        else: 
            dp[i][j] = max(dp[i - 1][j],value + dp[i - 1][j - weight])
            

print(dp[n][k])

⭐️ 문제 추천

백준 12865 - 평범한 배낭

🔥 응용 - 동전 거스름돈 문제

• 거스름돈을 최소한의 동전 개수로 주는 문제로, 배낭 알고리즘을 사용하여 풀이할 수 있다.
• 다른 점이 있다면 이 문제는 물건을 중복해서 사용할 수 있다는 점이다.

✏️ 풀이 방법

• 먼저 각 동전의 가치를 배열로 나타낸다.
• 이 배열을 coins라하고 거슬러 주어야 할 금액을 changes라고 하자.

1. dp 배열 정의하기

• i번째 동전까지 고려하고, j원의 거스름돈을 돌려줄 때 최소 동전 개수를 dp[i][j]로 정의

2. 점화식 세우기

• 거스름돈 j를 동전으로 나눈 나머지가 0이라면
  • 그 동전을 j//coins[i] 만큼 넣을 수 있음
• 거스름돈 j를 동전으로 나눈 나머지가 0이 아니라면
  • 동전 금액이 거스름돈보다 클 경우는 넣을 수 없음
    • 위 인덱스에 저장된 값 저장
  • 동전 금액이 거스름돈 보다 작은 경우
    • 그 동전을 한개 넣고 남은 금액(dp[i][j-coin[i]])에 최적화된 값을 더한 것과, 위 인덱스에 저장된 값 비교하여 최솟값 저장

3. dp[n][amount]에 최종 결과가 저장된다. (n은 동전의 종류)

• 처음 dp 배열을 매우 큰 숫자로 설정했을 경우, 주어진 동전으로 거스름돈을 줄 수 없으면 그 숫자가 저장되어 있다.

📍 코드 작성

coins = list(map(int, input().split()))  # 동전 
n = len(coins)  # 동전 종류
changes = int(input())  # 거슬러주어야 할 돈
dp = [[10001 for _ in range(changes+1)] for _ in range(n+1)]
for i in range(1, n+1):  
    for j in range(1, changes+1):
        # 나머지가 0이라면 -> 그 동전 넣을 수 있음 
        if j%coin[i] == 0: 
            dp[i][j] = j//coins[i] 
        # 나머지가 0이 아니라면 -> 몫 만큼 넣고 남은 금액 생각하기 
        else:
        	# 동전금액이 거스름돈보다 크면 넣을 수 없음
            if j < coins[i]:  
            	# 위에 저장된 값 저장
                dp[i][j] = dp[i-1][j]
            # 넣을 수 있으면
            # 위에 저장된 값과 계산한 값 비교하여 최솟값 저장
            else:
                dp[i][j]=min(dp[i-1][j],1+dp[i][j-coin[i]])
                
if dp[N][K] == 10001:
    print('불가능')
else:
    print(dp[N][K])

⭐️ 문제 추천

백준 11047 - 동전 0
백준 2293 - 동전 1
백준 2294 - 동전 2

댓글과 좋아요 그리고 의견 감사합니다 ♥️