배열(array)과 행렬(matrix), 벡터(vector)
배열(array)은 컴퓨터에서 일반적으로 사용하는 개념으로 수를 포함한 어떤 데이터의 묶음을 의미한다. 1차원으로 묶은 수를 수학에서 벡터(vector)라 부르며 행만 구성된 것을 행백터, 열만으로 구성된 것을 열벡터라 부른다. 2차원으로 묶은 수를 수학에서 행렬(matrix)이라 부르고, 우리가 알고있는 수많은 행열 계산식에 사용된다.
numpy에서는 배열로 계산의 기본을 수행하지만 좀더 편리한 계산을 위해서 하위 자료형으로 matrix(행렬)를 지원하고 있다.
Q. 파이썬 Numpy에서 배열과 행렬의 차이가 뭐지?
A. array는 수를 포함한 여러 자료의 묶음, matrix는 계산을 위한 수의 다차원 묶음이다.
배열(array)은 파이썬 뿐만아니라 일반적으로 컴퓨터 언어에서 여러종류의 데이터의 묶음을 의미하며, 행렬(matrix)는 이들중 다차원으로 수를 묶은 것을 의미한다.
우리가 수학에서 사용하는 matrix는 엄밀하게 행렬이며 파이썬에서는 numpy라이브러리의 matrix자료형으로 정의 또는 변환하여 사용하면 보다 손쉽게 행렬계산을 수행 할 수 있다.
numpy 라이브러리에서 matrix 자료형은 array 자료형에서 상속된 하위클래스 개념이며, 수학계산에서 좀더 편리하게 사용하기 위해 matrix 자료형으로 변환하여 사용하면 좋다. 이렇게 생성한 matrix는 좀더 편리하게 수많은 계산식을 사용할 수 있으나, 꼭 matrix로 변환해서 연산할 필요는 없다. 다만 몇가지 연산에서 다른 결과를 나타낼 수 있
행렬(matrix)을 사용하면 배열(array)보다 연산이 간단함
matrix 자료형은 array형 보다 손쉽게 행렬곱 (matrix multiplication, dot product; matrix*matrix) 연산과 복소공액 행렬(conjugated matrix; matrix.H) , 전치행렬(transpose matrix; matrix.T), 역행렬(Inverse matrix; matrix.I) 등 연산을 편리하게 사용 할 수 있다. 즉, 연속해서 수식을 만들어 연산을 수행하는 경우에 함수를 사용하면 불편하고, 이해도도 떨어지게된다. 이럴때 수기로 표현하는 것과 가능한 유사한 형태의 표기를 사용하면 매우 편리할 것이다. 이러한 편리함을 위해 matrix 자료형을 사용하게 되는 것이다.
배열(array)과 행렬(matrix), 벡터(vector) 의 생성
간략히 배열을 생성하는 방법은 numpy.array()함수를 사용하면 된다.
>>> import numpy as np
>>> np.array([[1,2],[3,4]])
array([[1, 2],
[3, 4]])행벡터와 열백터의 생성은 아래와 같이 1차원 리스트를 입력하는 방법으로 응용하면 된다.
>>> np.array([1,2,3])
array([1, 2, 3])
>>> np.array([[1],[2],[3]])
array([[1],
[2],
[3]])열벡터를 행벡터에서 만들어주는 또다른 방법은 ndmin의 변수를 주어 2차원 배열로 변경하고 .T 속성을 사용하면 된다.
>>> a=np.array([1,2,3],ndmin=2)
>>> print(a)
[[1 2 3]]
>>> a.T
array([[1],
[2],
[3]])a=[1,2,3]은 파이썬에서 배열이 아닌 list자료형이다. numpy에서 배열은 리스트형을 array()함수로 변환하여 만드는 것이다. 아래의 코드를 보고 의미를 한번 확인해 보자.
>>> b=[1,2,3]
>>> type(b)
<class 'list'>
>>> b
[1, 2, 3]
>>> c=np.array(b)
>>> type(c)
<class 'numpy.ndarray'>
>>> c
array([1, 2, 3])배열(array)과 행렬(matrix)의 생성과 변환
행렬을 생성하기위해서는 크게 배열을 생성하여 행렬로 변환하는 방법과 한번에 행렬을 생성하는 두가지 방법이 있다. 한번에 생성하는 것이 편리해보이지만 꽤 많은 함수가 배열(array)형태를 입력변수로 사용하므로 행렬을 사용하여 변환하는 방법이 더 유용하기도 하다.
배열은 아래와 같이 변환한다.
>>> import numpy as np
>>> a=np.array([[1,2],[3,4]])
>>> a
array([[1, 2],
[3, 4]])
>>> b=np.asmatrix(a)
>>> b
matrix([[1, 2],
[3, 4]])여기서 a는 배열이고, b는 행렬이다. asmatrix()함수를 사용하여 배열(array)를 행렬(matrix)로 변환할 수도 있고, 처음부터 matrix()함수로 정의할 수도 있다.
>>> np.matrix([[1,2],[3,4]])
matrix([[1, 2],
[3, 4]])
>>> np.mat([[1,2],[3,4]])
matrix([[1, 2],
[3, 4]])matrix()함수는 mat()라고 약어로 사용하여도 동일하게 동작한다.
배열(array)과 행렬(matrix) 연산 결과의 차이
행렬(matrix)이 아닌데도 배열을 사용하여 arrayarray와 같이 를 사용할경우 에러가 발생하는 것이 아니라 다른 결과를 나타내기 때문에 논리적인 오류를 발생할 수 있다.
a=(1324), b=[1324],
>>> a*a
array([[ 1, 4],
[ 9, 16]])
>>> np.dot(a,a)
array([[ 7, 10],
[15, 22]])
>>> b*b
matrix([[ 7, 10],
[15, 22]])>>> b*b
matrix([[ 7, 10],
[15, 22]])배열형에서는 연산으로 배열곱이 잘 수행되는 것을 볼 수 있다. 이러한 문제로 dot()함수를 쓰자는 사람들이 있을수 있지만, 연속된 많은 계산을 해야하는 경우 행렬의 곱 은 매우 유용하게 사용할 수 밖에 없다. 논리적 오류가 발생되지 않도록 주의하자.
이런 실수와 편이성을 높이기 위해서 Python 3.5버전 이상에서 부터는 배열형에서 행렬곱을 @을 사용하여 구현할 수 있도록 되었다.
Creating Arrays (배열 생성)
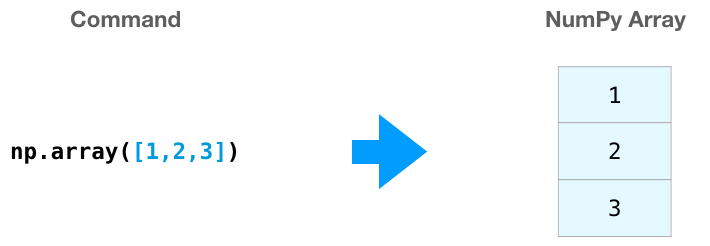
파이썬 리스트를 np.array()에 전달하여, NumPy 배열(즉, 강력한 ndarray)을 생성할 수 있습니다. 이 케이스에서 파이썬은 오른쪽에 보이는 배열을 생성합니다.
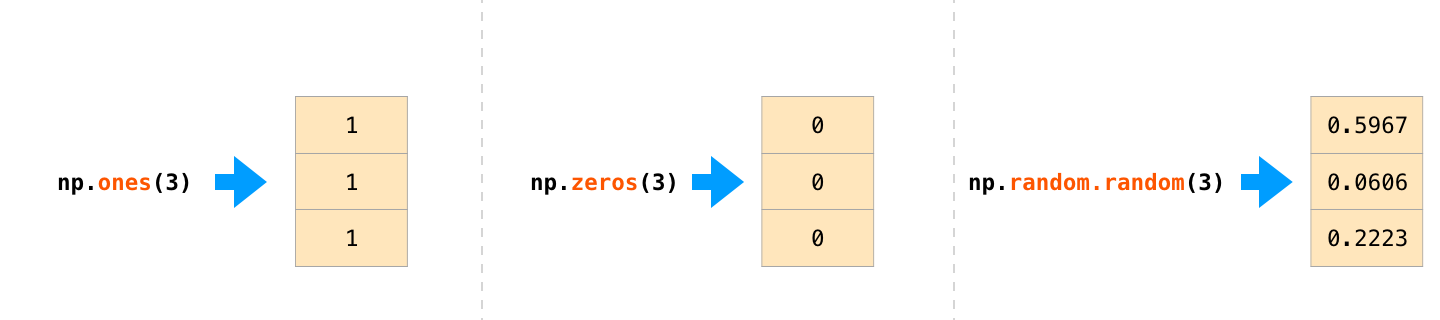
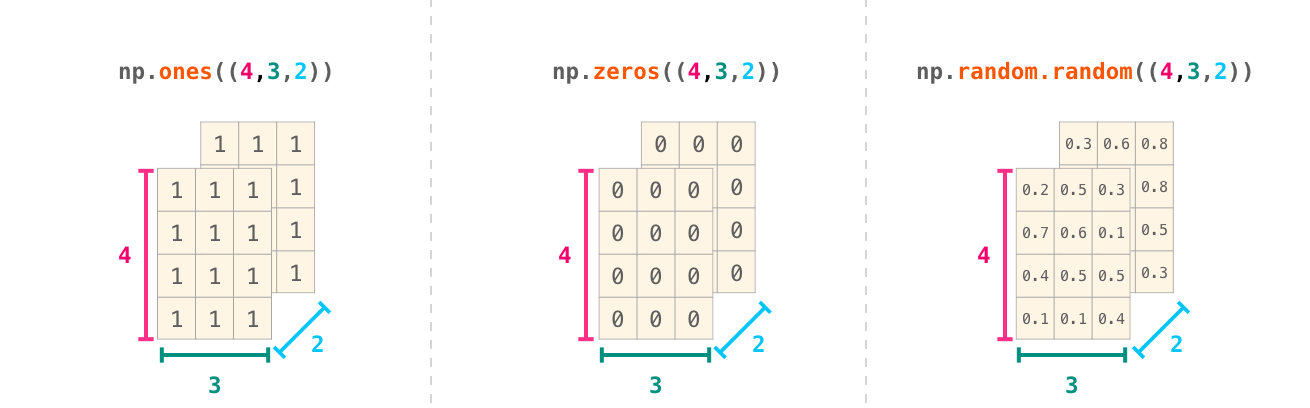
NumPy가 배열의 값을 초기화해주기를 바라는 케이스들이 종종 있습니다. NumPy는 이런 경우에 ones(), zeros(), random.random()과 같은 메서드를 제공합니다. 우리는 생성하기 원하는 element의 개수만 전달하면 됩니다:
Array Arithmetic (배열 산술연산)
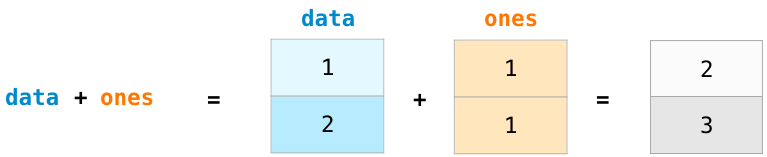
NumPy 배열의 유용성을 설명하기 위해 두 개의 NumPy 배열을 생성합니다. data와 ones라고 부르겠습니다:

position-wise 덧셈(즉, 각 행마다의 값들을 더하기)은 data + ones를 입력하면 됩니다. 간단합니다.
이런 방식으로 할 수 있는 것은 덧셈 뿐만이 아닙니다:

배열과 하나의 숫자값을 연산하고 싶을 때도 종종 있습니다 (우리는 이 것을 벡터와 스칼라간 연산이라고 부릅니다). 예를 들어, 마일로 표현된 거리 값을 가지고 있는 배열을 킬로미터로 변환하려고 한다고 가정해 보겠습니다. 간단하게 data 1.6라고 하면 됩니다:

NumPy가 이 연산()이 곱셈이 각 셀에서 수행되어야 한다는 것을 의미하는 것임을 이해하는 방법을 주목/확인해보세요. 그 컨셉을 브로트캐스팅이라고 합니다
Indexing (인덱싱)
파이썬 리스트에서 슬라이싱을 할 수 있는 모든 방법으로 NumPy에서도 인덱싱과 슬라이싱을 할 수 있습니다:

Aggregation (집계)
NumPy의 추가적인 이점은 집계 함수(aggregation function)들입니다.

min, max, sum 뿐만아니라 평균을 구하는 mean, 모든 element들을 곱한 결과를 구하는 prod, 표준 편차를 구하는 std, 다른 많은 연산들을 얻을 수 있습니다.
In more dimensions (더 높은 차원)
현재가지 우리가 살펴본 예제들은 1차원인 벡터들이었습니다. NumPy의 정수는, 우리가 지금까지 배운 능력들을 어떤 차원에도 적용할 수 있다는 것입니다.
Creating Matrices (배열 생성)
아래와 같은 모양의 파이썬의 중첩 리스트를 전달하여, NumPy가 이를 나타내는 행렬을 생성하도록 할 수 있습니다:
np.array([[1,2],[3,4]])
우리가 생성하려는 배열의 차원을 기술하는 튜플을 (파라미터로) 전달한다면, (ones(), zeros(), random.random() 등) 위에서 살펴본 메서드들을 사용할 수 있습니다.

Matrix Arithmetic (행렬 산술연산)
두 행렬의 크기가 같다면, 산술연산자 (+-*/)를 사용해서 행렬을 더하거나 곱할 수 있습니다. NumPy는 연산을 position-wise로 처리합니다:
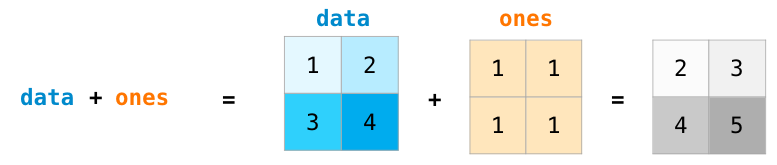
(행렬이 오직 1개의 열 또는 1개의 행을 가지고 있는 경우 등) 서로 크기가 다른 차원이 1개인 경우에만, 크기가 다른 행렬에 대해 이러한 산술 연산을 수행할 수 있습니다. 이 경우에 NumPy는 연산에 브로드캐스트를 적용합니다.

Dot Product (내적)
산술 연산과의 주요 차이점은 내적을 사용한 행렬 곱셈의 경우입니다. NumPy는 행렬에 다른 행렬과 내적 연산을 수행하는데 사용할 수 있는 dot() 메서드를 제공합니다:

행렬의 차원 정보를 그림 하단에 추가하여, 두 행렬이 서로 마주하는 면이 서로 같은 차원을 가지고 있어야 함을 강조했습니다. 이 연산을 아래와 같이 시각화하여 표현할 수 있습니다.

Matrix Indexing (행렬 인덱싱)
인덱싱과 슬라이싱은 행렬을 다룰 때 더 유용합니다:
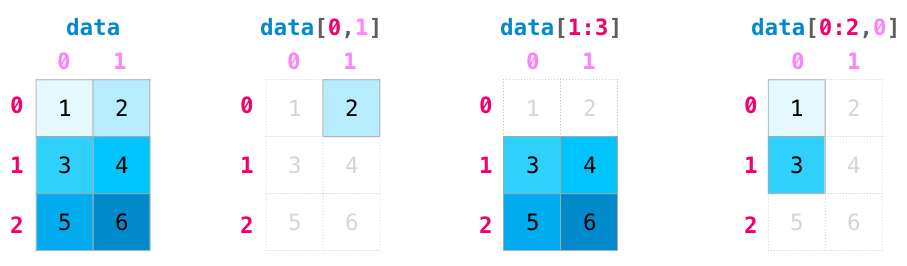
Matrix Aggregation (행렬 집계연산)
벡터를 집계했던 것과 동일한 방법은 행렬도 집계 연산을 할 수 있습니다:

행렬의 모든 값을 집계할 수 있을 뿐만 아니라, axis 파라미터를 사용하여 행 또는 영을 집계할 수도 있습니다.

Transposing and Reshaping (전치 및 재구조화/재배열)
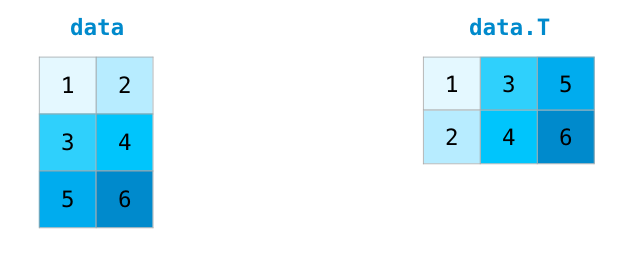
행렬을 다룰 때 일반적으로(많은 경우) 회전을 시킬 필요가 있습니다. 우리가 두 행렬에 내적을 취할 필요가 있거나 두 행렬이 공유하는(맞대는) 차원을 맞출 필요가 있을 때입니다. NumPy 배열을 행렬의 전치를 구하는 T라는 편리한 기능을 가지고 있습니다.
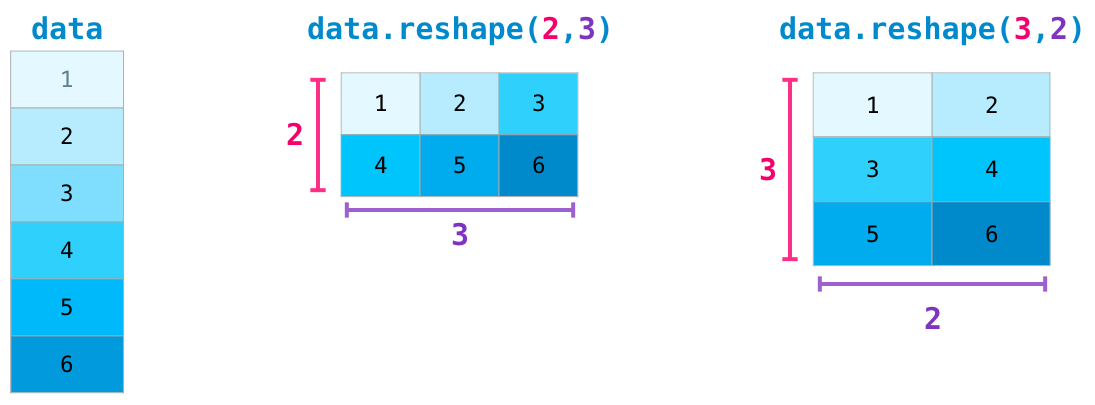
고급 유즈케이스(use case)로, 특정 행렬의 차원을 서로 바꾸는(switch) 필요를 느낄 수 있습니다. 데이터셋과 다른 입력이 있고, 그 입력이 특정 shape일 것을 모델이 기대하는 머신러닝 어플리케이션에서 종종 발생합니다. NumPy의 reshape() 메서드는 이러한 케이스에서 유용합니다. 원하는 행렬의 차원을 전달하기만 하면 됩니다. 만약 -1을 차원 값으로 전달하면, NumPy는 그 행렬의 정보를 기반으로 정확한 차원 값을 계산해냅니다.
Yet More Dimensions (한층 더 높은 차원)
NumPy는 앞서 언급한 모든 것을 모든 차원수에 대해 수행할 수 있습니다. 중심이되는 자료 구조를 ndarray(N-Dimensional Array; N-차원 배열)이라고 부르는 이유입니다.

많은 방법들 중에서, 새로운 차원을 다루는 방법은 콤마(,)를 NumPy 함수의 파라미터에 추가하는 것입니다.
array([[[1., 1.],
[1., 1.],
[1., 1.]],
[[1., 1.],
[1., 1.],
[1., 1.]],
[[1., 1.],
[1., 1.],
[1., 1.]],
[[1., 1.],
[1., 1.],
[1., 1.]]])Practical Usage (실질적인 사용법)
마무리입니다. 다음은 NumPy가 도움이 될 만한 몇가지 유용한 것들의 예입니다.
Formulas (수식)
행렬과 벡터를 다루는 수학적인 공식을 구현하는 것은 NumPy를 고려해야 하는 주요 사용 사례입니다. 이 것은 왜 NumPy가 과학적 파이썬 커뮤니티에서 사랑받는 이유 입니다. 예를 들어, 회귀 문제를 다루는 지도학습 머신러닝 모델의 중심인 평균 제곱 오차 수식을 고려해보세요:
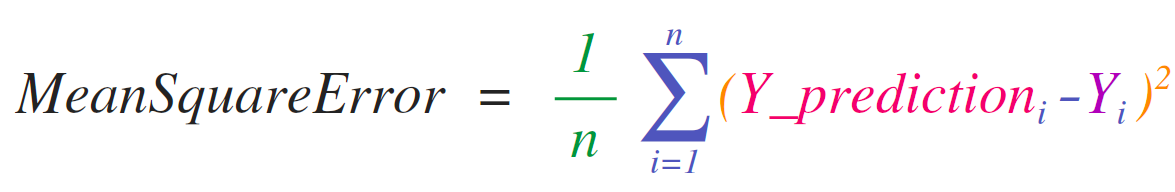
NumPy에서 이 것을 구현하는 것은 간단합니다:

이 것의 정수는 NumPy가 predictions와 labels이 한개던 천개던 몇개의 값을 가지고 있던지 간에 신경쓰지 않는다는 것입니다 (그 것들이 서로 같은 크기이기만 하다면). 다음 코드에서 4개의 연산을 순차적으로 단계별로 실행하는 예제를 살펴볼 수 있습니다:

predictions 및 labels 벡터는 모두 3개의 값을 가지고 있습니다. 이 것은 n이 3임을 의미합니다. 뺼셈을 수행한 뒤, 다음과 같은 값이 나옵니다:

그런 다음 벡터에 있는 값들을 제곱합니다:

이제 이 값들을 더합니다:

해당 예측에 대한 에러 값이자 모델 품질에 대한 점수가 산출됩니다.
Data Representation (데이터 표현)
모델을 처리하거나 빌드하는데 필요한 모든 데이터 유형에 대해 생각해보십시오 (스프레드시트, 이미지, 오디오 등). 대부분의 경우 n-차원 배열의 표현과 완벽하게 적합합니다.
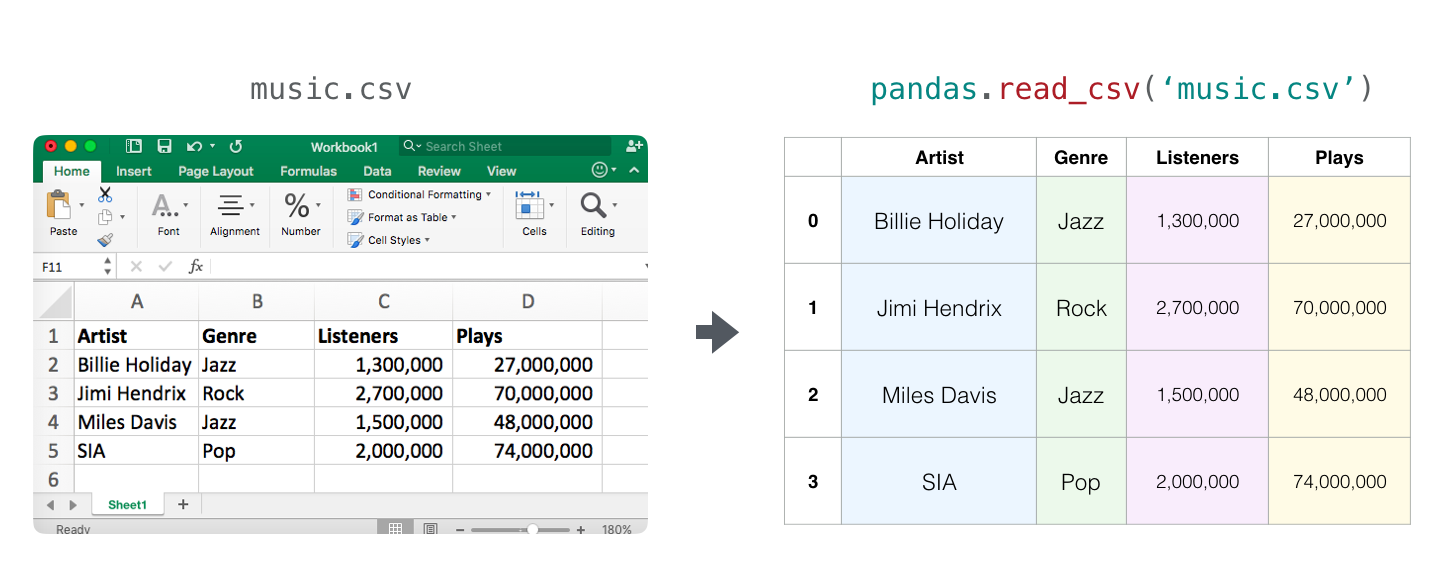
Tables and Spreadsheets
스프레드시트나 테이블은 2차원 행렬입니다. 스프레드시트의 각 시트가 행렬로 사용될 수 있습니다. 파이썬에서 이 것을 위한 가장 인기있는 추상화는 판다스 데이터프레임이며, 이 것은 NumPy를 사용했고 그 위에 빌드한 것입니다.
Audio and Timeseries(시계열)
오디오 파일은 오디오 샘플들의 1차원 배열입니다. 각 샘플들은 오디오 신호의 작은 조각을 숫자로 표현한 것 입니다. CD품질 오디오는 초당 44,100 샘플을 가지며 각 샘플은 -32767 ~ 32767 사이의 정수 값을 갖습니다. CD품질 10초 WAVE 파일을 가지고 있다면, 10 * 44,100 = 441,000 샘플 길이의 NumPy 배열로 로딩할 수 있습니다. 오디오의 첫 1초를 추출하고 싶으신가요? audio라고 명명할 파일을 NumPy 배열로 단순히 로드하고 audio[:44100]를 가져오면 됩니다.
다음은 오디오 파일의 일부분입니다:
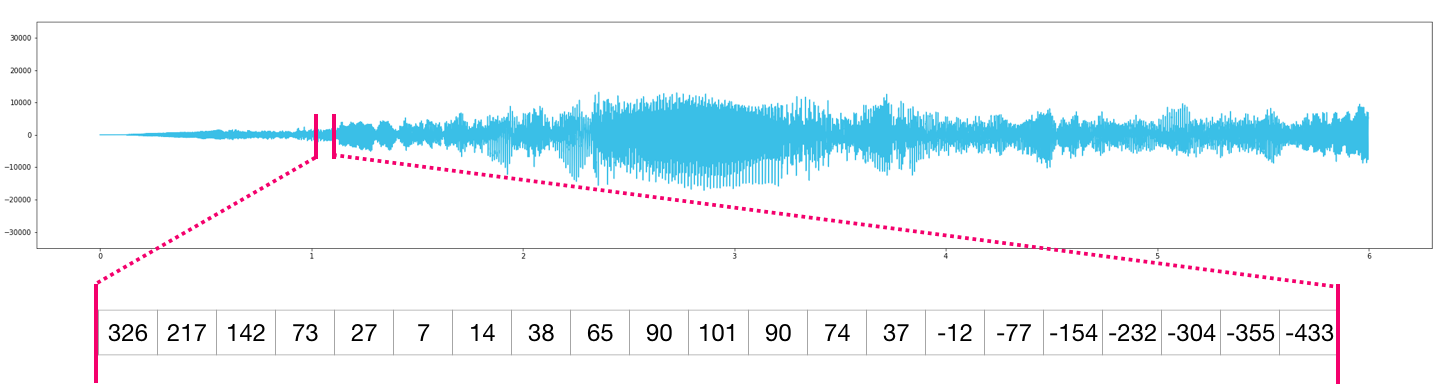
시계열 데이터도 동일합니다 (예를 들어, 시간에 걸친 주식 가격)
Images
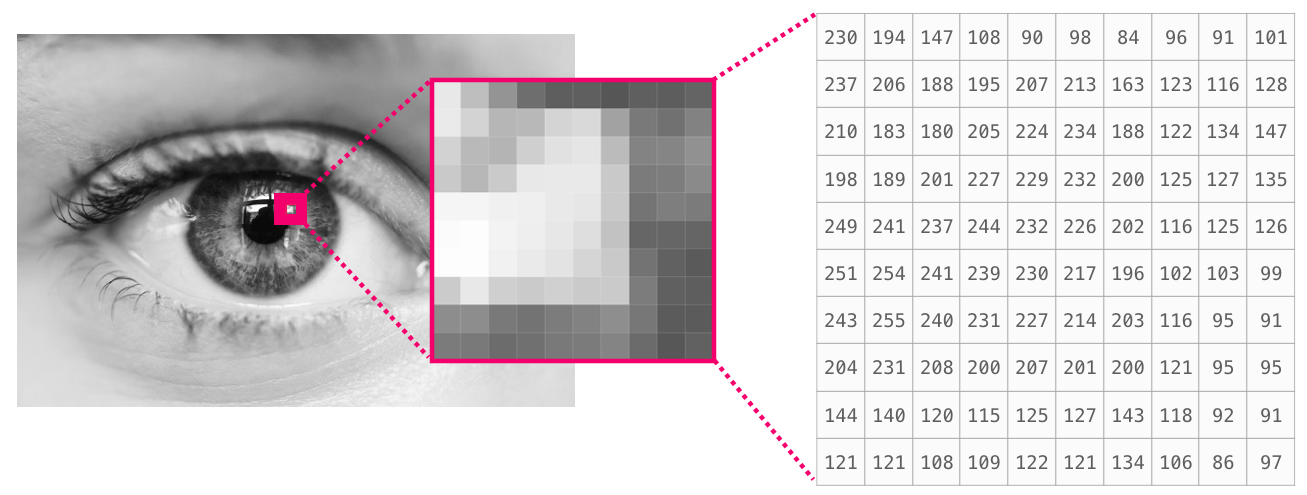
이미지는 (높이 x 너비) 크기의 픽셀 행렬입니다.
만약 이미지가 흑백(회색조라고도 함)이라면, 각 픽셀은 1개의 숫자로 표현됩니다(주로 0(검정), 255(흰색) 사이의 값). 이미지의 왼쪽 상단의 10 x 10 픽셀을 자르고 싶은가요? NumPy에게 image[:10,:10]라고 하시면 됩니다.
-
An image is a matrix of pixels of size (height x width).
-
If the image is black and white (a.k.a. grayscale), each pixel can be represented by a single number (commonly between 0 (black) and 255 (white)). Want to crop the top left 10 x 10 pixel part of the image? Just tell NumPy to get you image[:10,:10].
다음은 이미지 파일의 일부입니다:
만약 이미지가 컬러이미지라면, 각 픽셀은 3개의 숫자로 표현됩니다 - 빨강, 초록, 파랑 각각의 값. 이 경우에 우리는 3차원이 필요합니다 (각 셀이 한 숫자만 표현할 수 있기 때문에). 그래서 컬러이미지는 (높이 x 너비 x 3) 차원의 ndarray로 표현됩니다.
<div class="img-div-any-width" markdown="0">
<image src="/images/numpy/numpy-color-image.png"/>
<br />
</div>Language
만약 텍스트를 다룬다면, 얘기가 조금 달라집니다. 텍스트의 숫자 표현은 어휘(vocab; 모델이 아는 모든 고유한 단어 목록)이 만들어져야 하고 임베딩 단계가 있어야 합니다. 고대에 쓰여진 (번역된) 아래 인용구를 수치적으로 나타내는 단계를 살펴보겠습니다.
“Have the bards who preceded me left any theme unsung?” (“내 이전 음유시인들이 노래를 부르지 않고 남겨둔 주제가 있었던가?”)
모델은 이 전사 시인의 불안의 말(단어들)을 숫자로 나타내기 전에 대량의 텍스트를 볼 필요가 있습니다. 작은 데이터셋을 처리하여, (71,290 단어의) 어휘를 구축하는데 사용할 수 있습니다:

문장은 토큰(일반적으로 단어나 단어의 일부분)의 배열로 나뉩니다.

각 단어를 어휘 테이블의 id로 치환할 수 있습니다.

이 id들은 여전히 모델에게 많은 정보 가치를 제공하지는 않습니다. 그래서 모델에게 단어의 시퀀스를 공급하기 전에, 토큰/워드는 임베딩으로 대체될 필요가 있습니다 (이 예에서는 50 차원 word2vec 임베딩)

이 NumPy 배열이 [임베딩차원 x 시퀀스길이] 크기의 차원임을 알 수 있습니다. 실제로는 반대일 것이지만, 시각적 일관성을 위해 이렇게 표현하겠습니다. 성능 이유로, 딥러닝 모델은 첫번째 차원을 배치 사이즈로 남겨두는 경향이 있습니다 (왜냐하면 모델은 여러 예제를 병렬로 훈련하는 경우 빠르기 때문입니다). 이 것은 reshape()이 매우 유용해지는 명백한 케이스입니다. 예를들어, BERT와 같은 모델은 이 것의 입력을 [배치사이즈, 시퀀스길이, 임베딩_크기] shape의 입력을 예상합니다.
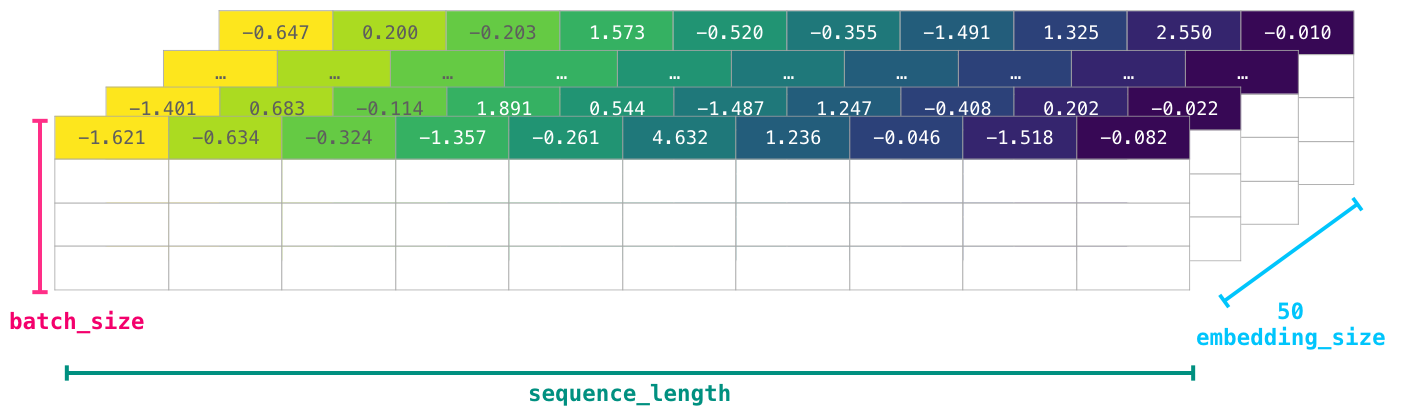
이제 모델이 유용한 작업을 수행할 수 있는 숫자 볼륨(단위)입니다. 다른 행은 비워 두었지만 모델이 학습(또는 예측)할 다른 예제(숫자값)들로 채워질 것입니다.
출처
https://numpy.org/devdocs/user/basics.broadcasting.html
https://techreviewtips.blogspot.com/2018/08/05-03-python-array-matrix.html
https://yganalyst.github.io/data_handling/memo_5/#1-2-3%EC%B0%A8%EC%9B%90-%EB%B3%80%ED%99%98
