🎯그래프 (Graph)

💡 그래프

그래프(G)는 정점(vertex)들의 집합 V와 이들을 연결하는 간선(Edge)들의 집합 E로 구성된 자료구조

###그래프 종류

1. 무향 그래프(undirected graph) vs 방향 그래프(directed graph)

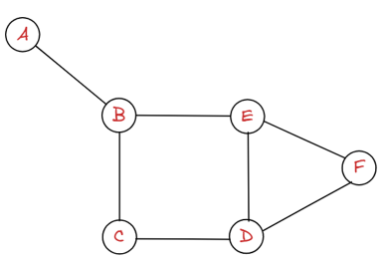
위와 같은 그래프는 A-> B로 갈 수 있으며 B->A로도 갈 수 있기에 무향 그래프(undirected graph)라고 한다. 따로 방향이 정해져 있지 않기 때문이다.

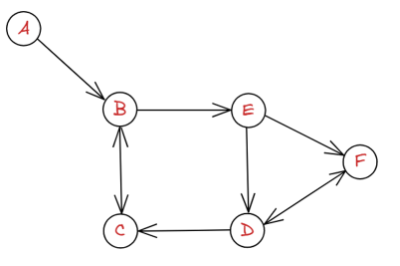
위와 같이 방향이 정해져 있는 그래프를 방향 그래프라 한다.

2. 단순 그래프(simple graph) vs 다중 그래프(multi-graph)

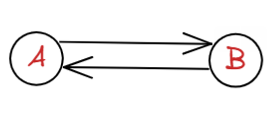
두 정점 사이에 indegree가 1개, outdegree가 1개인 그래프를 단순 그래프(simple graph)라고 한다. 코딩테스트에서는 주로 단순그래프를 다룬다.

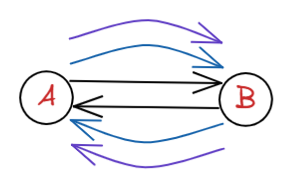
인접해 있는 두 정점 A,B의 관계에서 outdegree와 indegree가 2개 이상인 그래프를 다중그래프(multi-graph)라고 한다.

3. 가중치 그래프(weighted graph) vs 비가중치 그래프(unweighted graph)

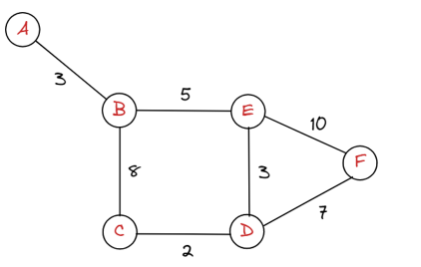
위와 같이 경로마다 비용(or 시간)이 다른 경우 가중치 그래프(weighted graph)라고 한다. 반대로, 모든 간선의 가중치가 동일한 그래프를 비가중치 그래프(unweighted graph)라고 한다.

가중치 그래프는 추후 다익스트라, 플로이드 워셜 알고리즘에서 쓰인다.

4. 순환 그래프(cyclic graph) vs 비순환 그래프(acyclic graph)

• 순환 그래프(cyclic graph)는 하나 이상의 사이클을 포함하는 그래프이다. 즉, 시작점으로 되돌아오는 경로가 존재하는 그래프이다.
• 비순환 그래프(acyclic graph)는 사이클이 없는 그래프이다. 즉, 어느 정점에서 시작하더라도 시작점으로 돌아오는 경로가 없는 그래프이다.

그래프 구현

1. 인접 행렬

int [][] matrix = {
{0, 1, 0, 0, 0, 0},
{1, 0, 1, 0, 1, 0},
{0, 1, 0, 1, 0, 0},
{0, 0, 1, 0, 1, 1},
{0, 1, 0, 1, 0, 1},
{0, 0, 0, 1, 1, 0},
};

2. 인접 리스트

간선이 적은 경우 대부분의 정보가 0으로 채워지기 때문에 행렬표현이 비효율적. 그런 경우엔 인접 리스트로 사용하면 좋다.

Map<String, List<String>> graph = new HashMap<>() {{
    put("A", Arrays.asList("B"));
    put("B", Arrays.asList("A", "C", "E"));
    put("C", Arrays.asList("B", "D"));
    put("D", Arrays.asList("C", "E", "F"));
    put("E", Arrays.asList("B", "D", "F"));
    put("F", Arrays.asList("D", "E"));
}};

3. 암시적 그래프

코테에서 가장 많이 활용되는 그래프.

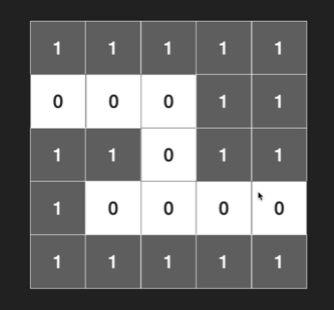
다음과 같이 흰색이 길이고, 검은색이 벽인 미로가 있다고 해보자. 벽에는 1의 값을, 길에는 0의 값을 넣어보자. 그 후 각 영역을 좌표로 표현할 수 있다.

int[][] graph = {
		{1, 1, 1, 1, 1},
		{0, 0, 0, 1, 1},
		{1, 1, 0, 1, 1},
		{1, 0, 0, 0, 0},
		{1, 1, 1, 1, 1}
};

위의 표현 방식의 경우 연결 관계를 직접적으로 나타내지는 않았으나, 상하좌우가 연결되어있다는 것을 암시적으로 알 수 있다.

이 그래프의 값들을 row와 col 변수명을 통해 graph[row][col] 배열로 만든다. 즉, (2,3)에 있는 값을 알고 싶으면 graph[2][3]을 알면 된다.

🎯BFS(Breadth First Search)

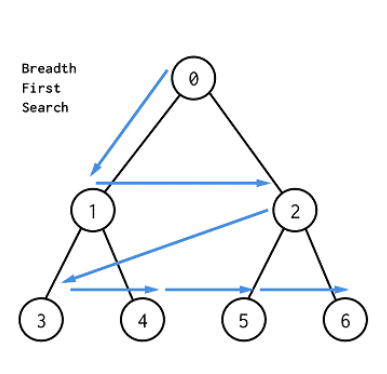
그래프 탐색 중너비 우선 탐색. 루트 노드(or 다른 임의의 노드)에서 시작해서 인접한 노드를 먼저 탐색하는 방법. 두 노드 사이의 최단 경로 혹은 임의의 경로를 찾고 싶을 때 이 방법을 선택한다.

💡 특징
1.어떤 노드를 방문했었는지 여부를 반드시 검사해야 한다. -> 이를 검사하지 않을 경우 무한루프에 빠질 위험이 있다.
2.방문한 노드들을 차례로 저장한 후 꺼낼 수 있는 자료 구조인 큐(Queue)를 사용한다. 즉 선입선출(FIFO)원칙으로 탐색.

🎯DFS(Depth First Search)

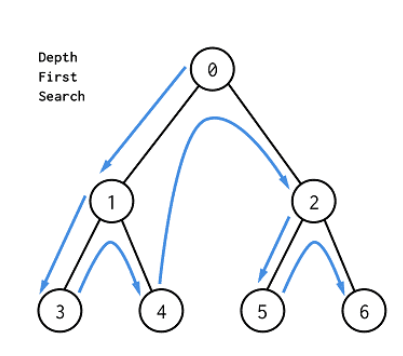
그래프 탐색 중 깊이 우선 탐색.루트 노드(or 다른 임의의 노드)에서 시작해서 다음 분기(branch)로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방법. 모든 노드를 방문하고자 할때 이 방법을 선택한다.

💡 특징
1.자기 자신을 호출하는 순환 알고리즘의 형태를 갖고 있다.
2.BFS와 마찬가지로 어떤 노드를 방문했었는지 여부를 반드시 검사해야 한다. ->이를 검사하지 않을 경우 무한루프에 빠질 위험이 있다.

🎯코딩테스트 활용

그래프 문제는 아래 템플릿 코드를 활용해서 해결하자. 이 템플릿 코드를 외운 다음, 이것을 기본 틀로 해서 아래 주석처리한 부분을 채워서 사용하자.

• 예시 그래프

public static void makeGraph() {
    graph.put(0, Arrays.asList(1, 3, 6));
    graph.put(1, Arrays.asList(0, 3));
    graph.put(2, Arrays.asList(3));
    graph.put(3, Arrays.asList(0, 1, 2, 7));
    graph.put(4, Arrays.asList(5));
    graph.put(5, Arrays.asList(4, 6, 7));
    graph.put(6, Arrays.asList(0, 5));
    graph.put(7, Arrays.asList(3, 5));
}

---

• BFS

Set<String> bfs(Map<String, List<String>> graph, String start) {
    Set<String> visited = new HashSet<>();
    visited.add(start);
    Queue<String> queue = new ArrayDeque<>();
    queue.add(start);

    while (!queue.isEmpty()) {
        String current = queue.remove();
		    // *---------------------------------------*
				// 그래프를 방문하며 처리해야할 일을 여기서 한다
				// (예시)
			  // if (current == value) {
				//     << 현재 노드가 특정 값을 만족할 때 해야할 일 >>
				//     return current;
				// }
		    // *---------------------------------------*
        for (String v : graph.get(current)) {
            if (!visited.contains(v)) {
                visited.add(v);
                queue.add(v);
            }
        }
    }
    return visited;
}

---

• DFS

static Set<String> visited = new HashSet<>();

static void dfs(Map<String, List<String>> graph, String current) {
    // *---------------------------------------*
		// 그래프를 방문하며 처리해야할 일을 여기서 한다
		// (예시)
	  // if (current == value) {
		//     << 현재 노드가 특정 값을 만족할 때 해야할 일 >>
		//     return current;
		// }
    // *---------------------------------------*
    visited.add(current);
    for (String v : graph.get(current)) {
        if (!visited.contains(v)) {
            dfs(graph, v);
        }
    }
}