
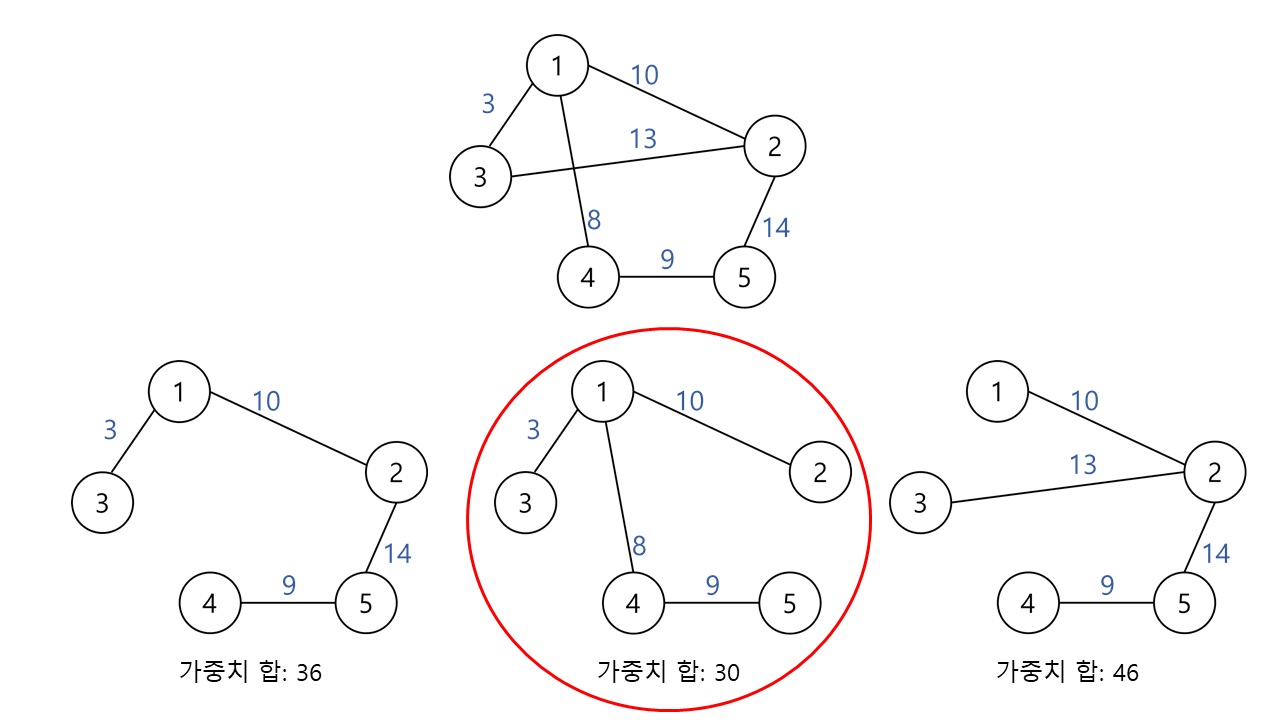
신장 트리는 그래프 내 모든 정점을 취하는 싸이클이 없는 그래프다.
최소 신장 트리(Minimum Spanning Tree, MST)는 그래프의 간선 가중치의 총합이 최소가 되는 신장트리다.
📌 greedy algorithm
mst를 구하기 위한 알고리즘 소개 전, 탐욕법(greedy algorithm)을 알고 가자. mst 알고리즘들 모두 알고리즘 설계 기법 중 하나인 탐욕법에 기초하기 때문이다.
탐욕법은 그 때 그 때의 최적으로 부분들을 향상시켜 결국 전체의 최적을 찾는 방법이다. 탐욕법을 사용하기 위해서는 2가지 조건이 있다.
탐욕적 선택 속성(Greedy-Choice Property)
- 앞선 선택이 뒷 선택에 영향을 주지 않는다.
최적 부분 구조(Optimal Substructure)
- 전체 최적은 부분 최적의 해결들로 구성된다.
📙 잔돈 거스름 예시
문제에 대한 예시 두 가지를 보며 탐욕법 이해를 돕자. 문제의 목표는 거슬러 줄 동전 개수를 최소화 하는 것이다.
예1
동전의 타입이 32원, 8원, 1원으로 구성되어 있다.
해당 문제에서 탐욕법 해결은 큰 동전부터 최대한으로 거슬러 준다. 즉, 큰 동전부터 시작하여 부분적 최적해를 구해 나간다.
해당 동전 구성에서 탐욕적 선택 속성이 있을까?
- O. 32원 이상의 금액에서 32원을 쓰지 않고는 최소의 것이 없기 때문이다.
예2
동전의 타입이 30원, 20원, 5원, 1원으로 구성되어 있다.
해당 동전 구성에서 탐욕적 선택 속성이 있을까?
- X. 30원 이상의 경우에 30원을 쓰지 않는 최소의 경우가 있다. 거스름돈이 40원이라면, 20원을 2개 쓰는 것이 최적이다.
결론적으로 탐욕법은 부분 최적을 해결해나가며 전체 최적을 구하는 알고리즘 설계 방법이다. 이어서 나올 mst 알고리즘 모두 탐욕법을 사용한다.
📌 Prim-Jarnik algorithm
프림 알고리즘은 단순 연결 양방향 가중그래프를 대상으로 하는 mst 알고리즘이다.
프림 알고리즘은 임의 정점을 시작으로 비어 있는 mst에 정점들을 삽입해 나가며 최종적으로 mst를 완성한다.
각 정점에 대해 라벨링을 하게 되는데 이 라벨값은 간선 가중치가 된다. 프림 알고리즘에서 각 반복은 mst에 속하지 않은 정점들의 라벨값 중 최소의 것을 mst에 포함시켜 나가는 탐욕법을 사용한다.
prim 알고리즘 의사코드
Alg PrimMST()
input simple connected weighted graph G, vertices number n,
edges number m
output mst
for each v in G.vertex() { //그래프 내 정점 초기화
distance(v) <- big integer number
parent(v) <- empty
}
start <- start vertex of G //시작 정점 선택, 초기화
label(start) <- 0
Q <- priority queue containing all vertices of G //우선순위 큐
using label as key
while(!Q.isEmpty) {
u <- Q.remove()
for each e in G.incidentEdge(u) {
z <- oppositeVertex(u, e)
if(z in Q && weight(u, z) < label(z)) {
label(z) <- weight(u, z)
parent(z) <- e
Q.replaceKey(z, weight(u, z))
}
}
}프림 알고리즘은 외부 메모리 우선순위 큐를 사용한다. 수행 최초에 그래프 내 모든 정점들을 우선순위 큐에 집어 넣고 시작하며, 큐의 정렬은 정점의 label에 의한다.
최초 반복 시도에서 remove되는 u는 start vertex다. u의 부착 간선들을 검사하면서 인접 정점 z를 구한다. 그 다음 z가 Q에 존재하고(최초에는 모두 Q에 존재할 것이다.) z의 라벨값이 (u, z) 간선의 가중치보다 크다면(최초에는 모든 경우에 z의 라벨값이 클 것이다.) z의 라벨을 갱신한다.
여기서 우선순위 큐의 메서드 replaceKey()는 큐의 재정렬을 수행한다. Q 내의 정점 라벨값이 수정됨에 따라 큐의 순위를 다시 잡아줘야 할 것이다.
prim 알고리즘 그림 수행 예시
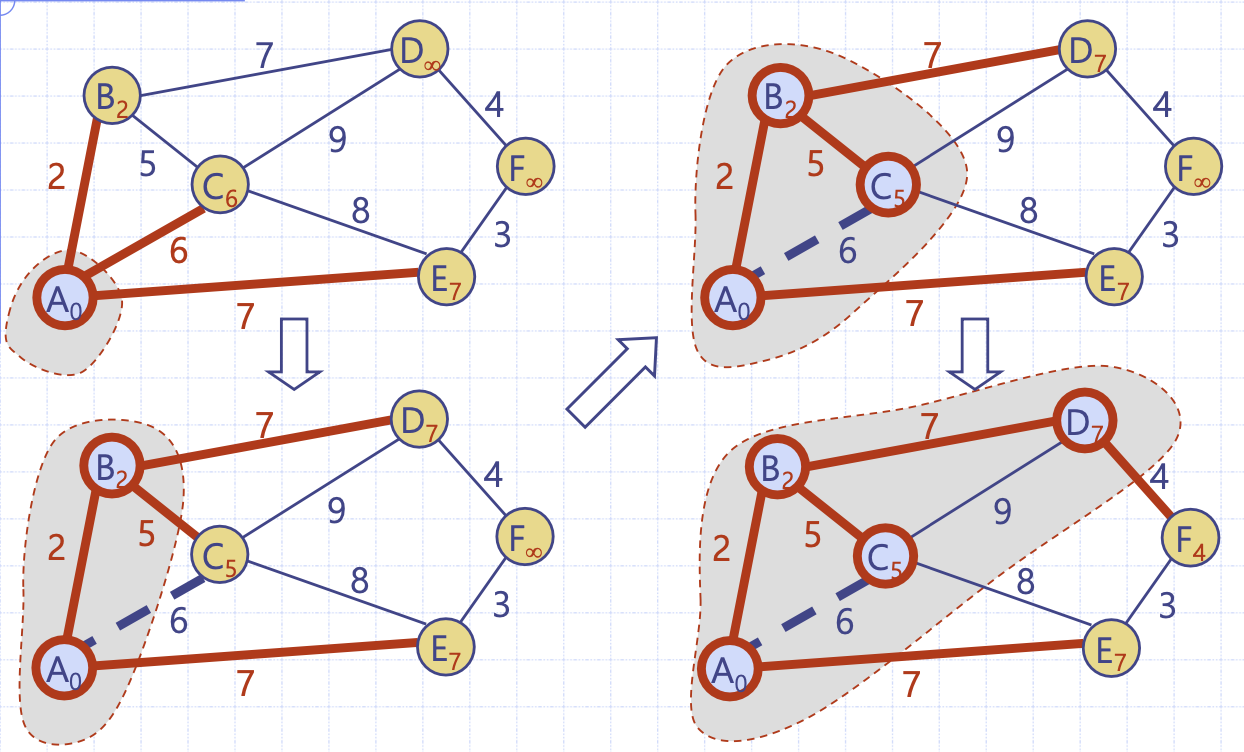
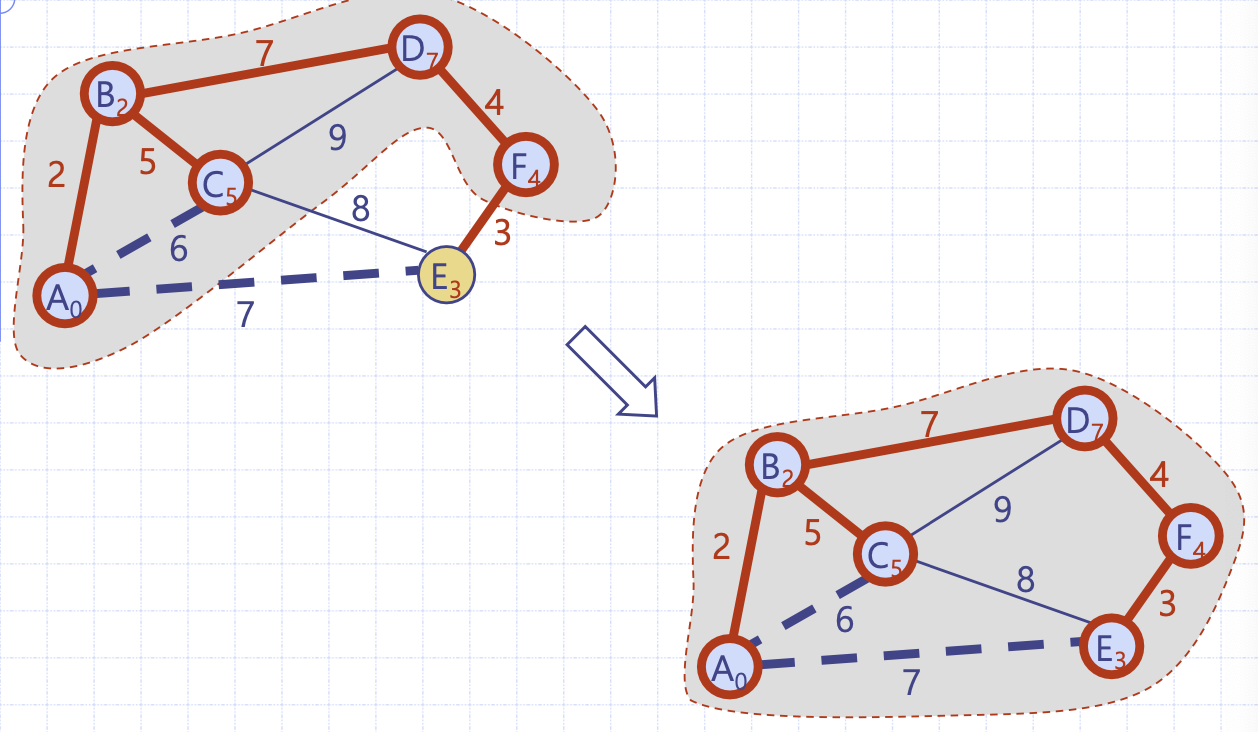
회색으로 표현된 부분은 비어 있는 mst가 수행함에 따라 mst를 최종 완성해 나가는 것을 보여준다.
먼저 A에서 시작한다 가정하자. A의 인접 정점에 대한 모든 라벨값을 갱신한다. 여기서 D와 F는 여전히 초기값을 갖는다.
그 다음 Q에서 가장 label 값이 작은, 가장 우선순위가 높은 B가 remove될 것이다. B의 인접 정점에 대한 모든 라벨값을 갱신한다.
그 다음 Q에서 C가 remove될 것이고 순차적으로 Q 내에 label값이 가장 작은 정점을 추출해 mst 외부 정점에 대한 라벨값을 갱신해가며 알고리즘이 수행된다.
prim 알고리즘은 bfs의 성격을 가지며 한 정점의 인접 정보를 활용하기 때문에 인접리스트 구조를 확보하는 것이 유리한 전략이다.
prim 알고리즘 + 그리디
그렇다면 프림 알고리즘은 탐욕법인가?
프림 알고리즘의 각 반복 라운드는 항상 mst 내부와 mst 외부를 이어주는 최소의 가중치 간선을 선택해 나가기 때문에 타당하다.
prim 알고리즘 성능
우선순위 큐가 힙 구조라면, 각 정점은 한 번 삽입되고, 한 번 삭제된다. O(n logn)
정점의 key는 자신의 degree만큼 변경될 수 있다. 변경에 따라 큐를 정렬해야 하므로 한 번 변경에 O(logn) 시간 소요된다. 전체적으로 간선 개수만큼 변경되므로 O(m logn)이다.
이 둘을 더한 O((n+m)logn)이 프림 알고리즘의 시간복잡도이나 정점의 개수 n은 단순 연결 그래프에서 간선 개수 m보다 작거나 같으니 O(m logn)이다.
프림 알고리즘은 외부 메모리 사용부터 bfs와 거의 유사하다. 그런데 bfs는 O(n+m)이지만, prim 알고리즘은 O(m logn)이다. bfs는 정점들이 큐에 차곡차곡 들어가 그 안에서 순서가 바뀌지 않기 때문이다.
참고
국형준. 알고리즘 원리와 응용. 21세기사, 2018.
https://velog.io/@suk13574/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-%EC%B5%9C%EC%86%8C-%EC%8B%A0%EC%9E%A5-%ED%8A%B8%EB%A6%AC
