이전까지의 다익스트라, 벨만포드, DAG 최단 경로 알고리즘은 모든 쌍이 아닌 단일점에서 출발하는 최단 경로를 구하는 알고리즘이다. 최단 경로 포스팅의 마지막은 그래프의 모든 정점 쌍 간의 최단 경로를 찾는 알고리즘을 학습한다.
음의 가중치가 없다면 다익스트라 알고리즘(O(V+E)log V or O(Elog V))을 정점 개수 V번 실행하여 O(VElog V)에 수행할 수도 있다.
음의 가중치가 있다면 벨만포드 알고리즘(O(VE))을 정점 개수 V번 실행할 수도 있다.
그러나 이번 포스팅에서는 dp를 사용해 모든 쌍에 대한 최단 경로를 구한다. 해당 방식은 음의 가중치가 있더라도 정확히 구할 수 있으며 dp를 사용해 모든 쌍 최단 경로를 이행적 폐쇄를 구하기 위해 사용했던 플로이드-마샬 알고리즘 방식으로 수행한다.
모든 쌍 최단 경로 의사코드
Alg allPairsShortestPath()
input graph G
output matrix D, s.t. D[i, j] is the distance from v[i] to v[j]
arbitrary numbering of all vertices of G //정점 순서 지정
for i<-1 to n { //matrix D 초기화
for j<-1 to n {
if(i = j) { //i=j, 거리 0
D[i, j] = 0
} else if((v[i], v[j]) in G.edge()) { //i->j 간선 있으면
D[i, j] <- weight(v[i], v[j])
} else { //간선 없으면
D[i, j] <- big number
}
}
}
for k<-1 to n { //dp 방식의 모든 쌍 최단 경로 구하기
for i<-1 to n {
for j<-1 to n {
D[i, j] <- min(D[i, j], D[i,k] + D[k, j])
}
}
}알고리즘은 정점들에 번호를 매기고 정점 간의 최단 경로를 나타내는 matrix D의 원소값을 초기화한다.
주의 깊게 볼 부분은 가장 아래의 삼중 반복문이다. 반복문은 모든 i->j에 대해서 최단 경로를 구한다. 반복문의 의미는 D[i, j]를 계산하는데에 k를 경유하여 가는 경로와 기존 원소값 중 작은 것을 D[i, j]로 취하는 동적 계획법이다.
기존의 D[i, j]는 v[i]에서 v[j]로 갈 때, 정점 k 이전 1 ~ k-1번까지를 경유해 가는 경로를 의미한다.
D[i, k] + D[k, j]는 v[i]->v[k]와 v[k]->v[j]의 경로다. Floyd-Marshall 알고리즘과 매우 유사하다.
그림 수행 예시
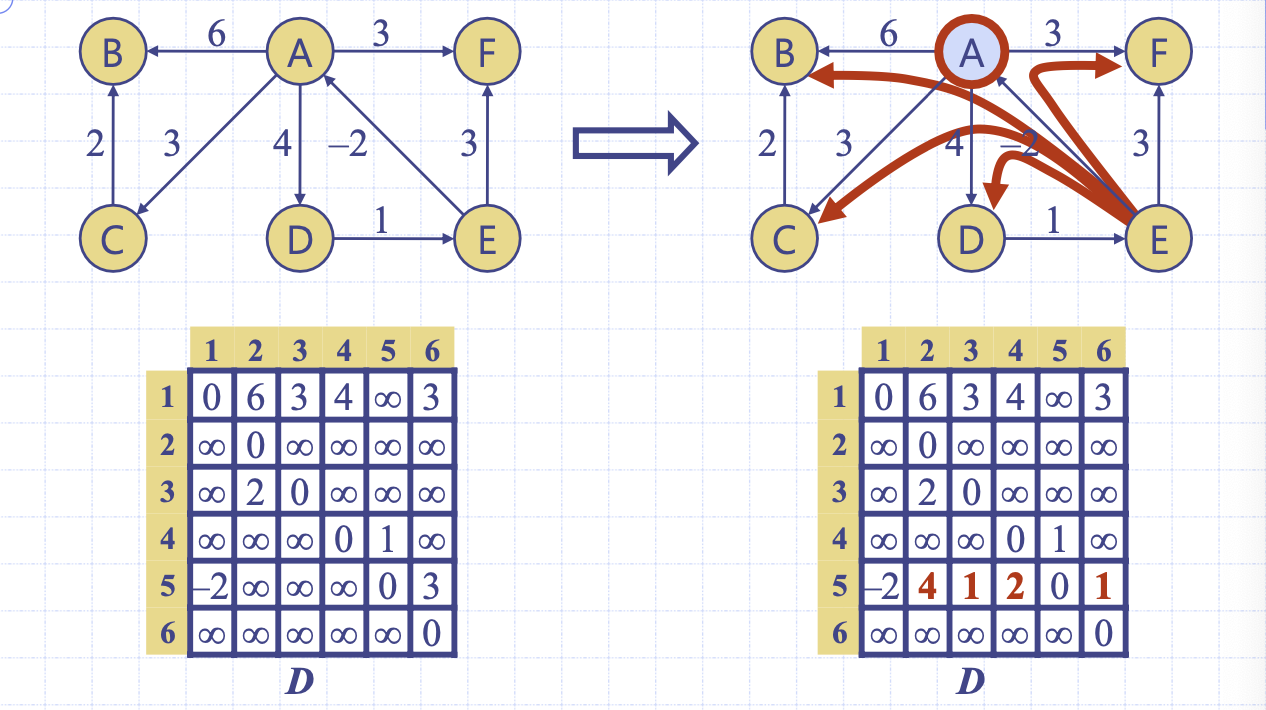
좌측 매트릭스는 초기화 상태다. 알파벳 순서대로 번호를 오름차순으로 지정했으며 자기 자신에게는 0, 존재하는 간선에 대해서는 간선의 가중치를, 존재하지 않는 간선에 대해서는 큰 값을 저장했다.
우측 매트릭스는 k가 1일 떄 즉, 1번 정점을 경유지로 하여 최단 경로값을 계산한다. i가 5(E)인 경우를 제외하면 A를 경유하는 정점은 없다.
k = 1 / i = 5 / j = 1: 5->1->1. -2로 변동 없다.
k = 1 / i = 5 / j = 2: 5->1->2. -2 + 6 = 4. 갱신한다.
k = 1 / i = 5 / j = 3: 5->1->3. -2 + 3 = 1. 갱신한다.
k = 1 / i = 5 / j = 4: 5->1->4. -2 + 4 = 2. 갱신한다.
k = 1 / i = 5 / j = 5: 5->1->5. x
k = 1 / i = 5 / j = 6: 5->1->6. -2 + 3 = 1. 갱신한다.
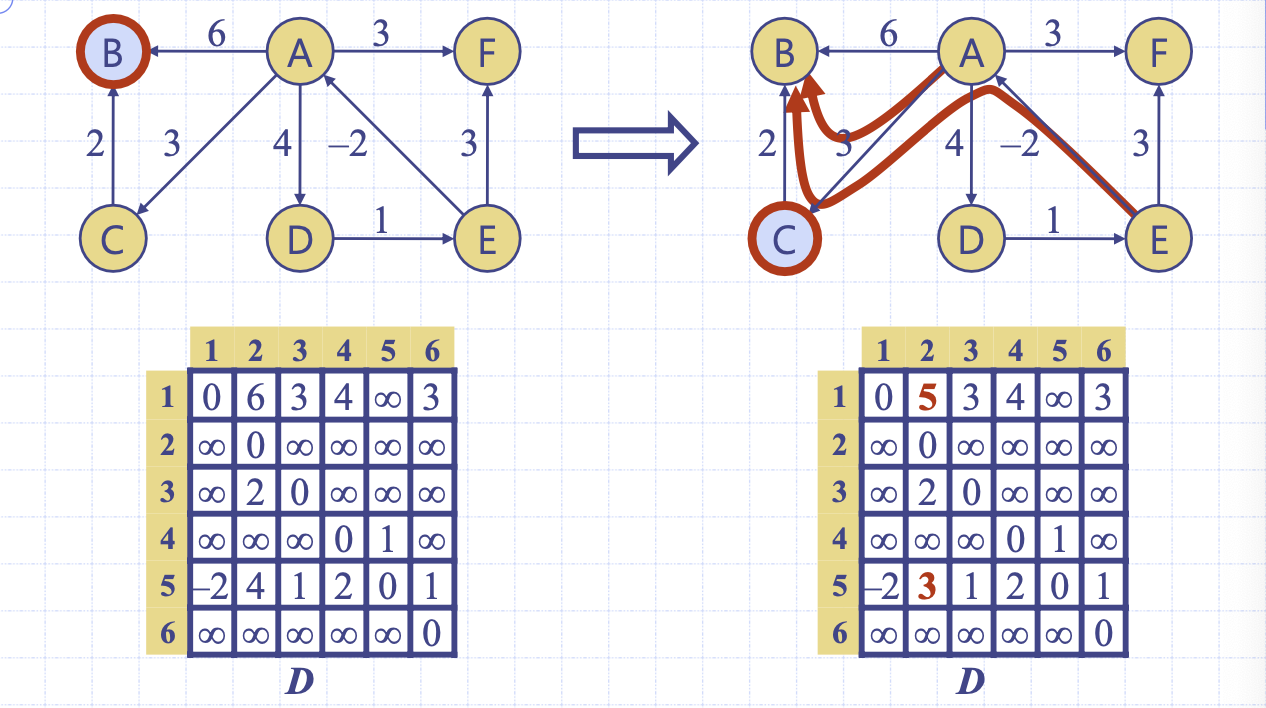
좌측 매트릭스는 k가 2일 때 즉, 2번 정점을 경유하는 최단 경로값을 계산한다. B에서 나가는 간선이 없기 때문에 매트릭스는 갱신되지 않는다.
우측 매트릭스는 C를 경유하는 최단 경로값을 계산한다.
k = 3 / i = 1 / j = 2: 1->3->2. D1, 3 + D3, 2 = 5. 갱신한다.
k = 3 / i = 5 / j = 2: 5->3->2. D5, 3 + D3. 2 = 3. 갱신한다.
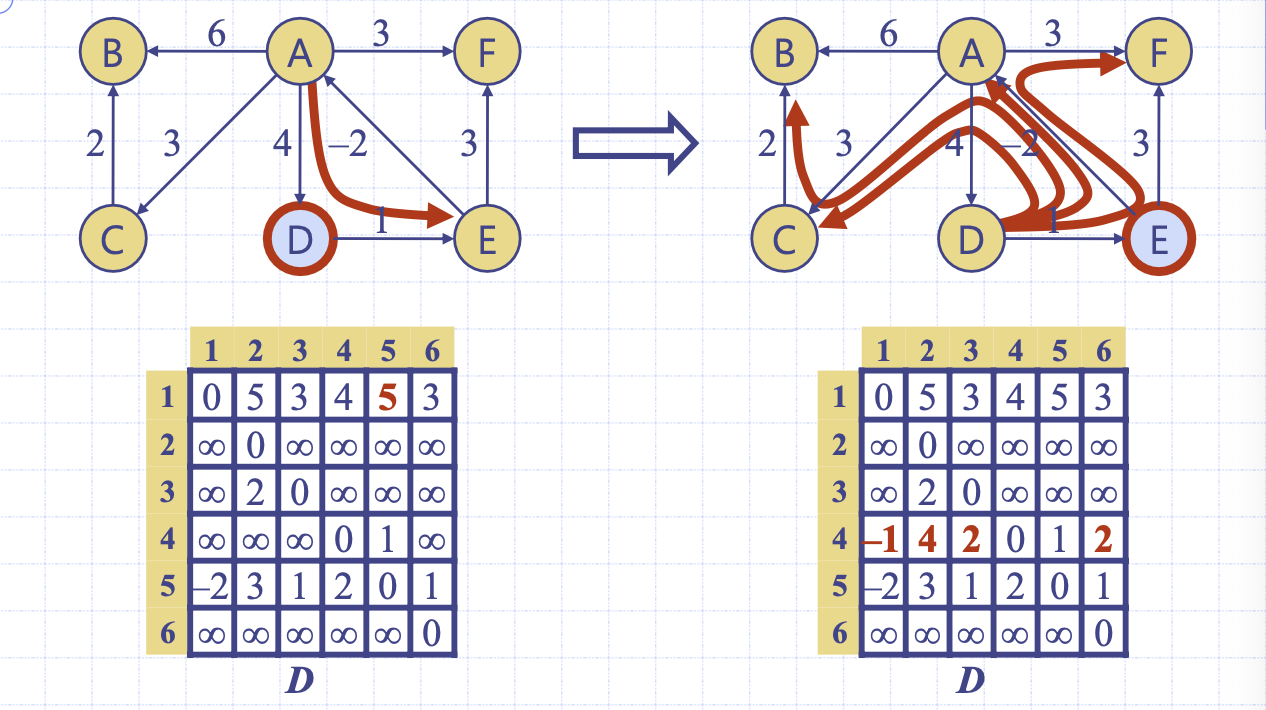
좌측 매트릭스는 D를 경유하는 최단 경로값을 계산한다.
k = 4 / i = 1 / j = 5: 1->4->5. D1, 4 + D4, 5 = 5. 갱신한다.
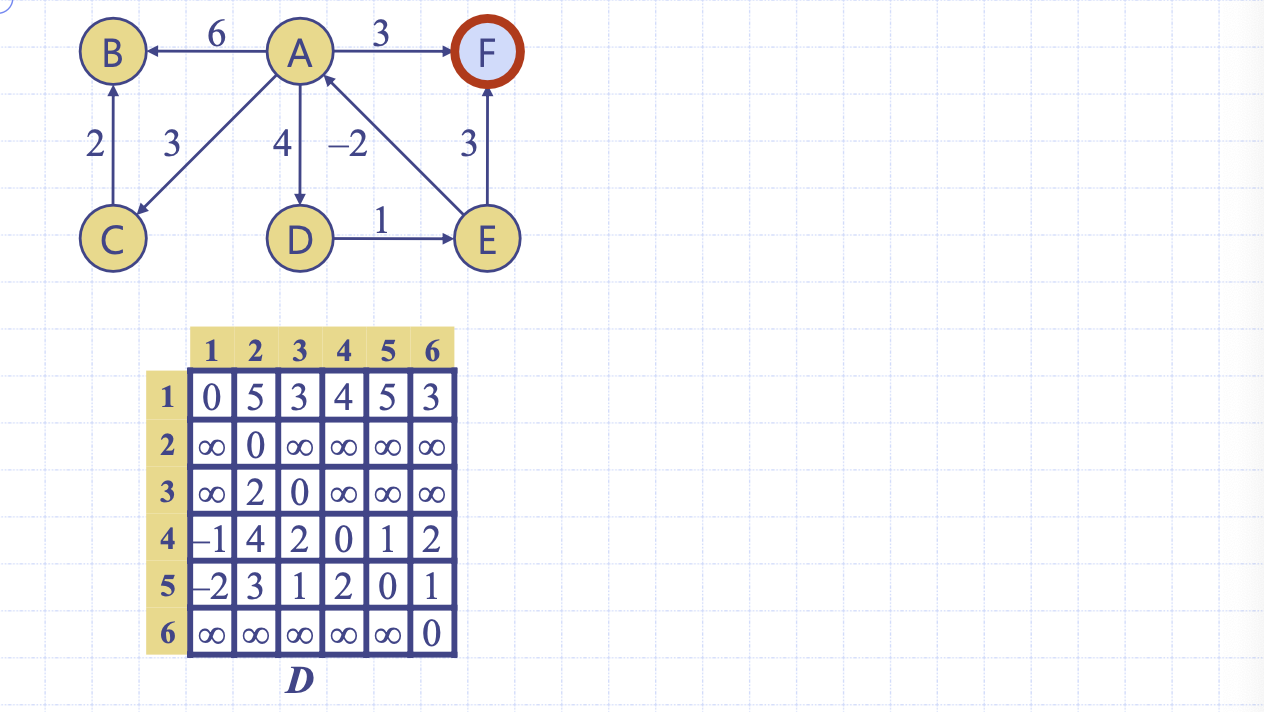
이렇게 최종적으로 dp를 활용해 모든 정점 쌍 간의 최단 경로를 구할 수 있다.
알고리즘 복잡도는 단순히 O(V^3)이다.
최단 경로 알고리즘
지금까지 다익스트라, 벨만포드, DAG을 이용해 최단 경로를 구하는 방법을 알아보았고 추가적으로 단일점이 아닌 dp를 활용해 모든 쌍에 대한 최단 경로를 구하는 것도 알아보았다.
다익스트라는 음의 가중치를 허용하지 않는다. 그래프가 연결 그래프라는 전제 하에 O(Elog V) 시간복잡도다.
벨만포드는 음의 가중치를 허용하지만 방향 간선이라는 조건이 붙는다. O(VE) 시간 소요된다.
DAG은 DAG의 특수성을 이용해 위상 순서로 최단 경로를 구한다. O(V+E) 걸린다.
제일 범용적으로 쓰이는 것은 벨만포드 알고리즘이다. 나머지는 음의 가중치가 없다는 조건, 그래프가 싸이클이 없는 방향 그래프라는 조건이 붙었을 때 벨만포드 알고리즘의 성능을 개선시킬 수 있다.
알고리즘 포스팅을 마치며
알고리즘 포스팅은 2023-2학기 알고리즘 강의를 들으며 배운 내용을 정리하는 차원에서 작성했다. 알고리즘 강의는 C언어로 진행되었는데 일부러 의사 코드로 포스팅을 이어간 것도 그런 차원이다. 원래의 계획은 강의도 들으며 + 강의 실습 문제도 해결하며 + 과제도 풀이하며 + 포스팅도 작성하며 + 관련 백준 문제도 풀면서 밀도 있게 시간을 보내려 했으나, AVL tree부터 실습 문제 해결 시간이 비약적으로 증가하더니 그래프로 들어와서는 백준은 커녕 포스팅도 작성할 수가 없었다. 그래서 몰아서 와다다 작성해버렸다.
저번 학기 자료 구조는 개강 전 책 한 권을 보고 들어갔더니 그렇게 쉬울 수 없었다. 주변에서 자구, 알고 그렇게 겁을 줬는데 긴장이 조금 풀린 느낌. 그게 문제였다. 해낼 수 있을 줄 알고 알고리즘은 개강 전까지 예습 한 번 안 하고 시작을 했는데 크게 당했다. 뭐 꾸역꾸역 잘 따라왔다만, 자료 구조 때와 달리 진도를 따라가면서 구멍이 숭숭 난 곳이 한 두 군데가 아님을 개인적으로 느끼고 있다.
마지막 주차 실습, 과제가 끝나고 dfs와 bfs 기초 문제를 java로 풀어봤다. 다른 사람 풀이와 비교해봤는데 데이터 구조 세팅하는 것이나 세부적인 풀이가 강의 내용과 차이가 분명 있었다. 역시 개념과 실전은 다른 건가? 이런 생각을.. 뭐 아무튼 코드 비교하면서 배움을 많이 얻고 있는 요즘이다.
강의 내용에 대한 알고리즘 포스팅은 끝이 났지만 종강 후 코테 준비하면서 이런 저런 문제에서 새로운 배움을 얻고 새로운 포스팅을 올릴 수 있으면 좋겠다. 내 생각이나 감상을 적은 것이 처음인 것 같은데 뭐 이번 학기 알고리즘은 끝! 이제 문제를 풀어보자! 끝!
참고: 국형준. 알고리즘 원리와 응용. 21세기사, 2018.
