📌 First normal form(1NF)
모든 애트리뷰트는 atomic values(원자값)를 가져야 한다.
각 튜플은 고유 식별자로 구분되어야 한다.
만약 테이블 내에 반복되는 그룹이 있다면, 원자성을 가진다고 볼 수 없다.
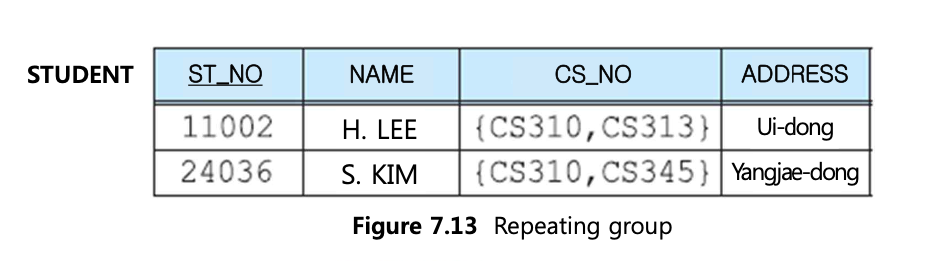
CS_NO 애트리뷰트는 원자값이 아니다.
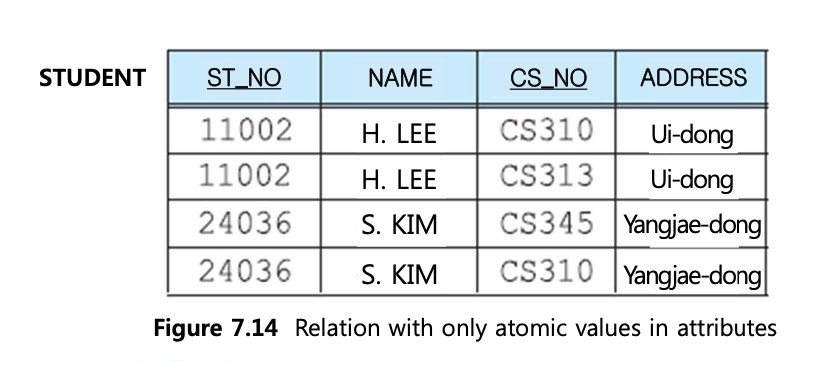
pk인 (ST_NO, CS_NO)에 의해 고유하게 식별되고 있지 않다. 테이블을 쪼개준다.

📙 1NF의 갱신 이상
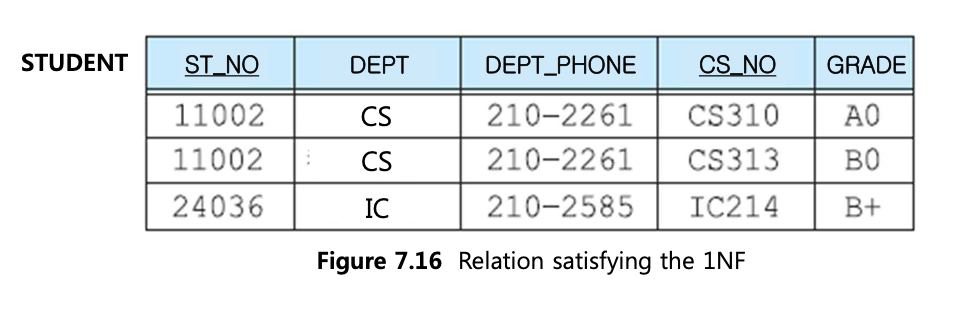
위 테이블은 모든 애트리뷰트가 원자값을 가지고 (ST_NO, CS_NO)를 통해 각 행이 고유하게 구별된다. 따라서 1NF를 만족한다. 그러나 1NF를 만족하더라도 갱신 이상은 발생할 수 있다.
수정 이상
- 만약 여러 학생이 소속된 DEPT의 DEPT_PHONE을 일부 튜플에서만 수정할 경우 데이터 일관성은 깨지게 된다.
삽입 이상
- 학생이 없는 특정 DEPT가 있는 경우, DEPT는 삽입될 수 없다.
- 학생을 NULL값으로 튜플을 삽입해야 할텐데 ST_NO가 pk이고 NULL값을 pk로 설정하게 된다면, 엔티티 무결성 제약 조건에 걸린다.
삭제 이상
- 부서에 남은 마지막 학생을 삭제한다면, 부서에 대한 정보도 같이 날라간다.
📙 1NF 갱신 이상 이유
여전히 갱신 이상이 발생하는 이유는 부분함수 종속성이 있기 때문이다.
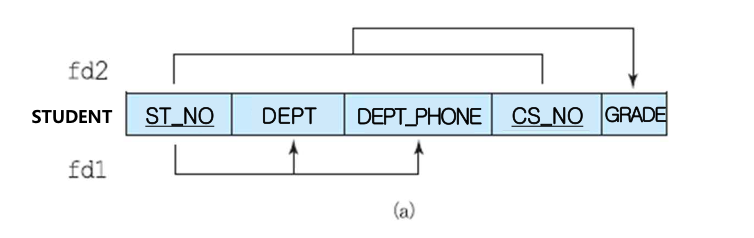
(ST_NO, CS_NO) -> GRADE : 완전함수 종속성
그 외 fd1은 기본키의 부분 집합에 의해 결정되는 부분함수 종속성이다. 부분함수 종속성은 2NF부터 relation decomposition을 통해 제거한다.
📌 Second normal form(2NF)
제 2정규화의 필요충분조건은 1NF를 만족하고 테이블 내 pk에 대한 완전함수 종속성을 포함하는 것이다.
기본키가 복합키인 경우에만 1NF가 2NF를 충족하는지 고려한다. 즉, 하나의 pk인 테이블이 1NF를 만족하면 2NF도 만족한다.
부분 함수 종속성
- 특정 속성이 pk가 아닌 속성에 종속되거나
- pk 구성 요소의 일부에만 종속되는 경우
📙 2NF의 갱신 이상
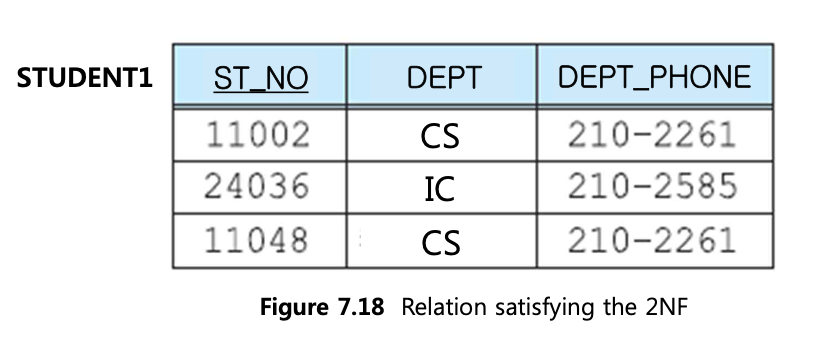
위 테이블은 1NF를 만족하고(원자값을 가짐) 완전함수 종속성을 만족한다.
수정 이상
- 여러 학생들이 속한 DEPT의 DEPT_PHONE을 변경할 경우, 모든 DEPT_PHONE을 뒤져가며 변경하지 않는 이상 데이터베이스 일관성이 깨진다.
삽입 이상
- 학생이 없는 새 DEPT를 삽입하려고 할 경우, pk를 NULL값으로 할 수 없기 때문에 삽입이 불가능하다.
삭제 이상
- 부서의 마지막 남은 학생을 삭제할 경우, 부서 정보가 날라간다.
📙 갱신 이상 이유
여전히 갱신 이상이 발생하는 이유는 이행적 함수 종속성이 있기 때문이다.
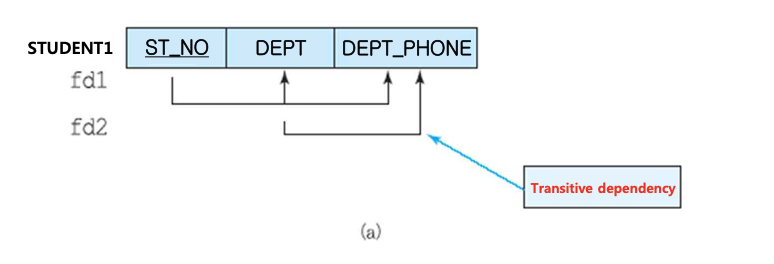
ST_NO는 DEPT와 DEPT_PHONE을 결정한다. 그러나 DEPT도 DEPT_PHONE을 결정한다. 이행적 함수 종속성의 제거는 3NF에서 고려한다.
📌 Third normal form(3NF)
제 3정규화의 필요충분조건은 2NF를 만족하고 테이블 내 pk에 대한 이행적 함수 종속성을 갖지 않는 것이다.
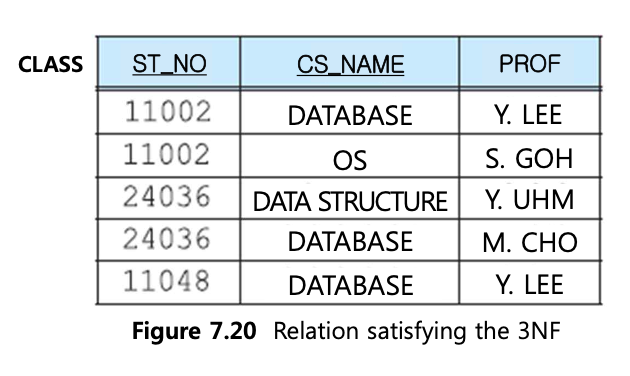
7.20 그림은 학생들은 여러 class를 들을 수 있고 교수들은 하나의 class만 가르친다는 요구사항이 있다.
위의 테이블은
1NF를 만족하고(원자값)
2NF를 만족하고(부분함수 종속성X, 완전함수 종속성O. key가 아닌 PROF 속성은 pk에 대해 FFD를 가짐)
3NF를 만족한다.(해당 속성은 pk에 의해 직접적으로 종속됨)
📙 3NF의 갱신 이상
수정 이상
- 여러 학생이 수강하는 class의 PROF이 변경될 때, 모든 학생의 튜플을 다 뒤져가며 PROF의 값과 CS_NAME을 바꿔주지 않으면 데이터 일관성이 깨진다.
삽입 이상
- 삽입할 class의 학생이 없을 때, ST_NO에 NULL을 삽입할 수 없기 때문에 해당 class의 PROF을 삽입할 수 없다.
삭제 이상
- 특정 class의 마지막 학생을 삭제할 때, class에 대한 교수 정보까지 삭제된다.
📙 갱신 이상 이유
여전히 갱신 이상이 발생하는 이유는 결정자가 pk 이외에 존재하기 때문이다. 후보키는 현재 pk인 (ST_NO, CS_NAME)과 (ST_NO, PROF)이다.
📌 BCNF
BCNF 정규화의 필요충분조건은 3NF를 만족하고 모든 결정자는 후보키여야 하는 것이다.
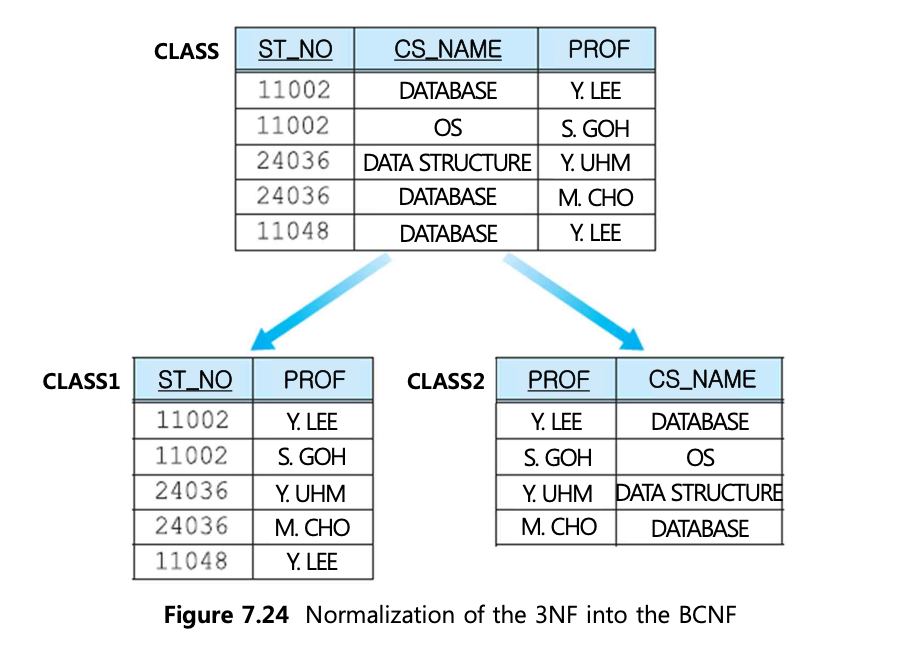
PROF은 후보키가 아니지만 CS_NAME을 결정한다. 대부분의 relation이 3NF를 만족하면 BCNF도 만족한다.
만약 3NF 테이블의 후보키가 1개라면 자동으로 BCNF도 만족한다.
3NF를 BCNF로 정규화하기 위해 키가 아닌 애트리뷰트(예시 PROF)와 그 애트리뷰트에 함수적으로 종속된 다른 속성(CS_NAME)을 하나의 테이블로 만든다. 그 다음 이 종속 관계의 결정자(PROF)가 그 테이블의 pk를 맡는다.
그 다음, pk의 구성요소로 만들었던 결정자(PROF)를 외래키로 만든다.
📙 3NF, not in BCNF 예시
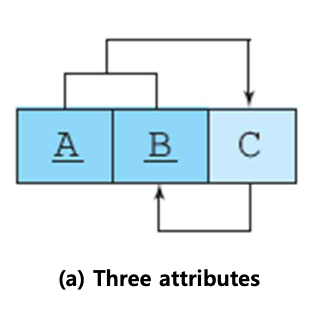
(A,B) -> C
C -> B
- C -> B인 테이블을 만든다.
- 그 후, 남은 pk 구성요소 A와 결정자 C를 기본키로 하는 테이블을 만들어 분할한다.
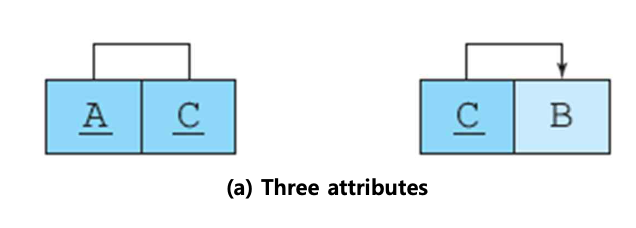
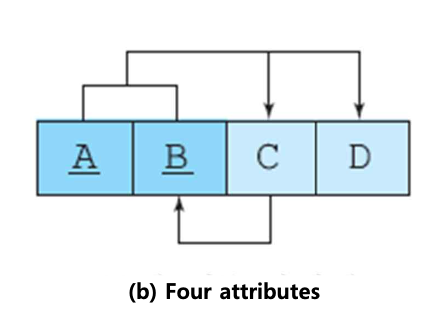
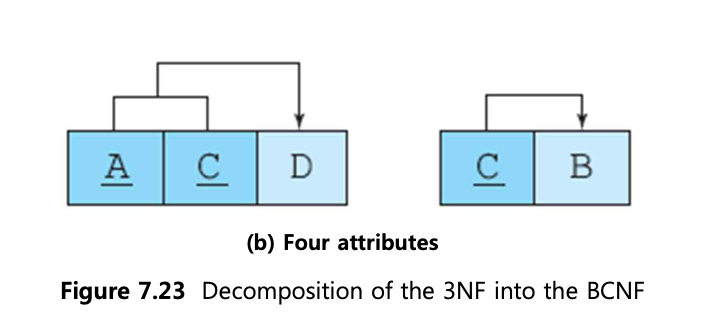
(A,B) -> C, D
C -> B
- C -> B인 테이블을 만든다.
- 그 후, 남은 pk 구성 요소 A와 결정자 C를 기본키로 하는 테이블을 만들어 분할한다.
📌 1NF ~ BCNF
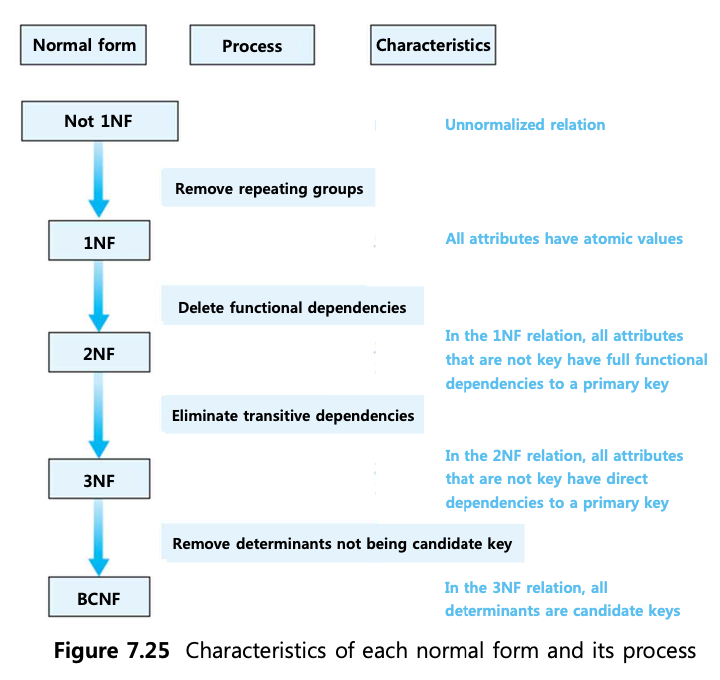
NOT 1NF -> 1NF
테이블의 애트리뷰트가 원자값을 갖도록 테이블을 분할한다.
결과 테이블: 모든 애트리뷰트는 원자값을 가진다.
1NF -> 2NF
부분함수 종속성을 제거한다.
결과 테이블: key가 아닌 모든 애트리뷰트는 pk에 대해 FFD를 만족한다.
2NF -> 3NF
이행적 함수 종속성을 제거한다.
결과 테이블: key가 아닌 모든 애트리뷰트는 pk에 직접적으로 종속된다.
3NF -> BCNF
후보키가 아닌 결정자를 제거한다.
결과 테이블: 모든 결정자는 후보키다.
