[프로그래머스] Lv.1 기사단원의 무기 Python

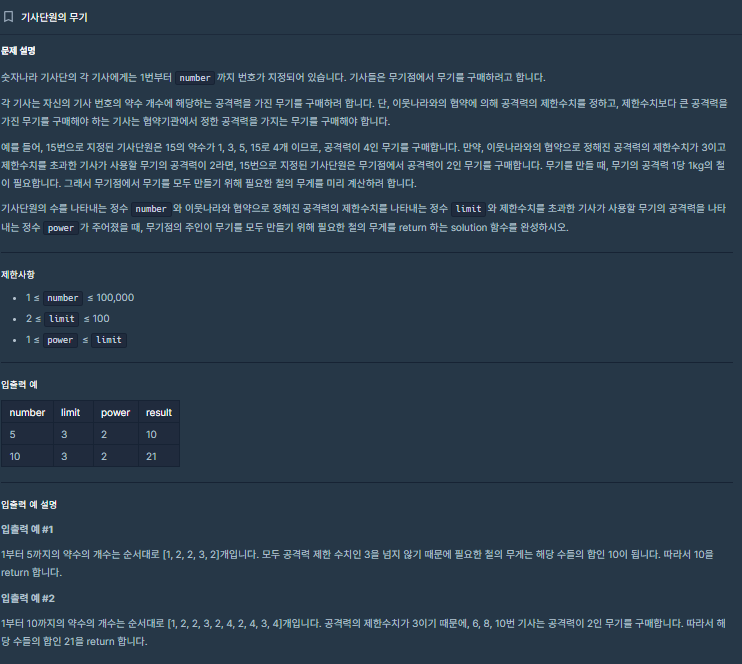
📍 문제 설명

📍 풀이 point

1) 1부터 지정된 기사단원의 수까지 각 수 별로 약수의 개수를 구한다.

2) 1부터 각 수까지를 기사단원수에서 나누어주고 나머지가 0인 경우를 약수로 판단하여 약수의 개수를 구한다(이렇게 하면 시간 복잡도가 높아 통과할 수 없다).

3) 약수의 개수에 limit를 넘는 수가 있는지 검사하고 넘는 수가 있다면 power로 바꿔준다.

4) 바꿔준 뒤 약수의 개수(공격력)을 다 더해주면 철의 무게를 구할 수 있다.

def solution(number, limit, power):
    num = []
     
    for i in range(1,number+1):
        count = 0
        # 약수 개수 구하기
        for j in range(1,+1):
            if i % j == 0:
                count+=1
        num.append(count)
        
    for z in range(len(num)):
        if num[z] > limit:
            num[z] = power
    
    return sum(num)

이 방법은 약수를 구할 때, 아래 코드 부분으로 인해 시간 복잡도가 O(N)이 되기 때문에 시간초과로 통과할 수가 없었다.

for j in range(1,+1):
            if i % j == 0:
                count+=1
        num.append(count)

따라서, 시간 복잡도를 줄이기 위하여 해당 부분을 아래 코드와 같이 변경하였다.

자연수 N의 약수를 구할 때 N은 항상 N = A * B 로 나타낼 수 있음을
고려하고, A를 구할 경우 그 짝이 되는 B는 자동으로 구할 수 있다는 것을 이용한다.

즉, N의 제곱근까지 반복문을 돌며 약수를 구하고 N을 해당 약수로 나눴을 때 해당 약수보다 크면 약수에 추가해준다.

(나는 이 부분을 이해하는데 좀 걸렸다. 복습 필수)

def solution(number, limit, power):
    num = []
     
    for i in range(1,number+1):
        count = 0
        # 약수 구하기 부분 수정 ver.
        for j in range(1,int(i**0.5)+1):
            if i % j == 0:
                count+=1
                if j < i//j:
                    count+=1
        num.append(count)
        
    for z in range(len(num)):
        if num[z] > limit:
            num[z] = power
    
    return sum(num)

이렇게 약수 구하는 부분을 변경해주면 시간 복잡도가 O(N^(1/2))로 줄어들기 때문에 통과할 수 있다.