정의와 성질
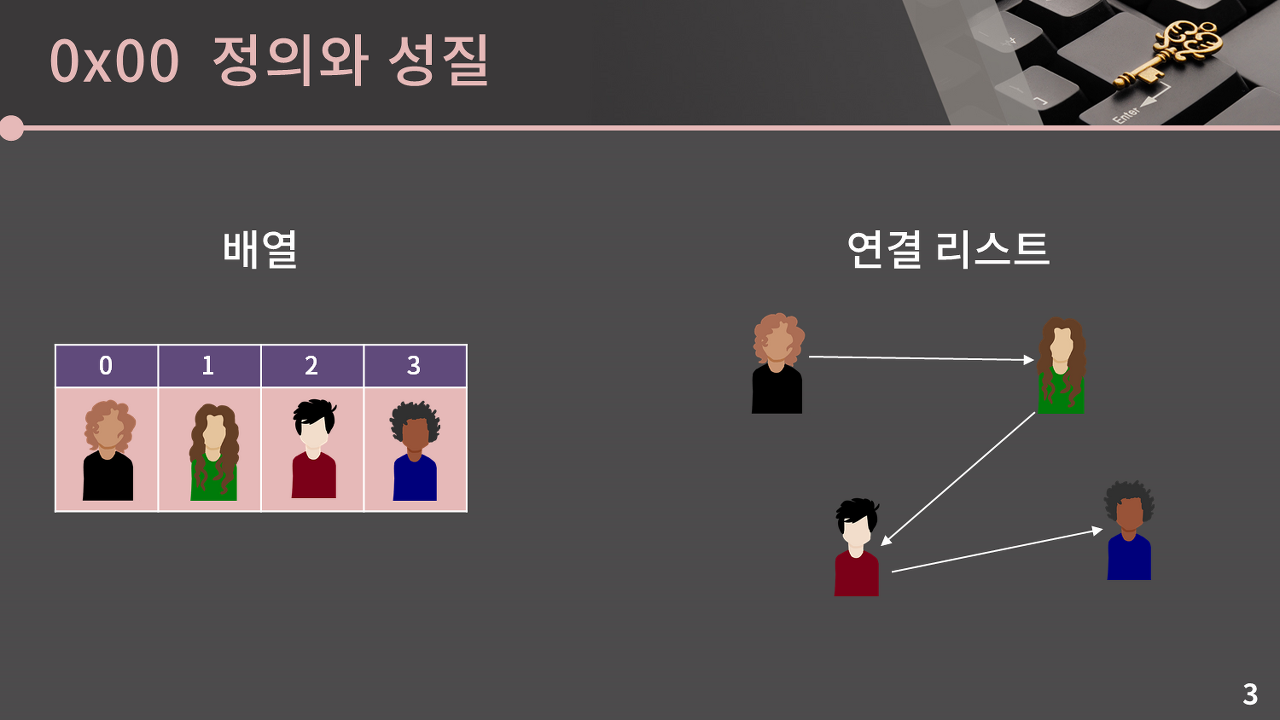
배열과 연결리스트의 성질을 비교하며 보자.
연결 리스트는 원소들이 저장될 때 그 다음 원소의 위치를 알 수 있는 자료구조입니다. 원소들의 위치는 배열과 다르게 이곳 저곳에 흩어져있다.
연결리스트의 성질
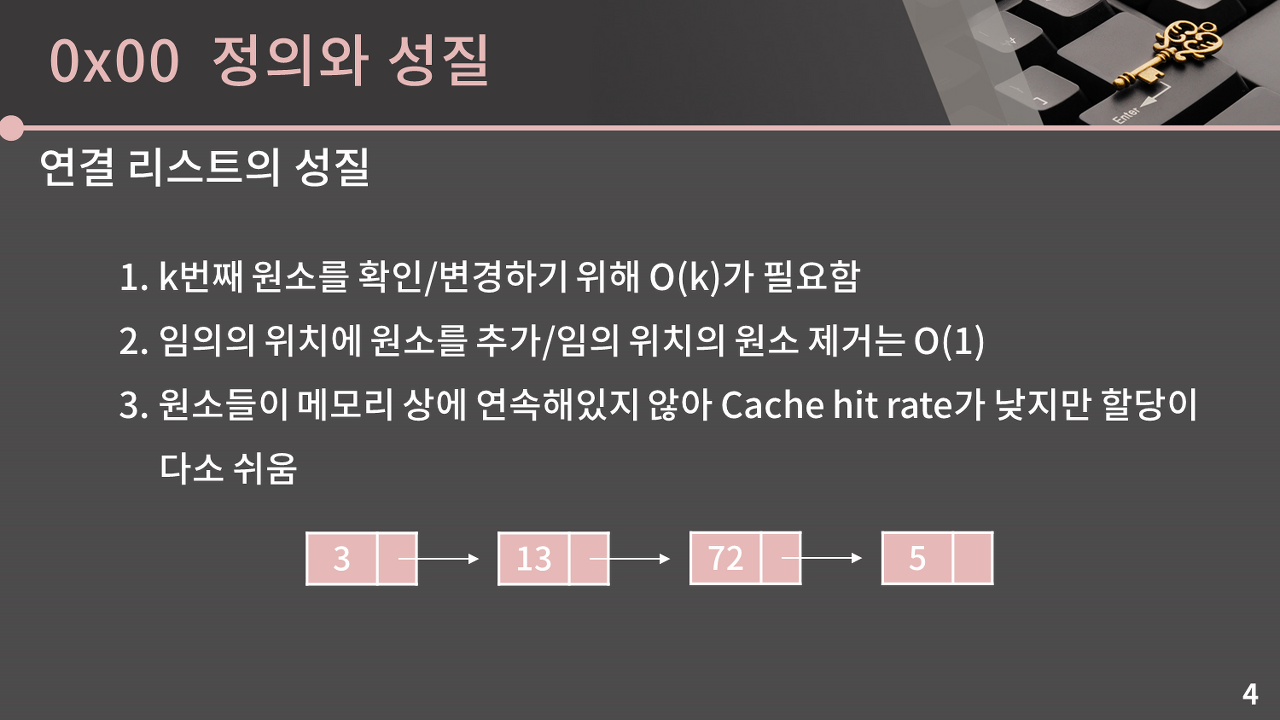
k번째 원소 찾기는 O(k)의 시간복잡도
연결 리스트의 구조 상 불가피한 부분이다.
그림은 3, 13, 72, 5를 저장하는 연결 리스트이고, 여기서 3번째 원소인 72를 찾고 싶으면 3을 거쳐서 13을 가고, 13을 거쳐서 72를 가야한다. 배열과 다르게 공간에 원소들이 연속해서 위치하고 있지 않기 때문.
임의의 위치에 원소를 추가, 제거는 O(1)의 시간복잡도
배열과 비교했을 때 큰 차이가 있는 성질이며 연결 리스트의 굉장히 큰 장점이다. 다음 챕터에서 더 자세히 살펴보자.
마지막으로 메모리 상에 데이터들이 연속해있지 않아서 Cache hit rate가 낮지만 할당이 쉽습니다. 물론 이 성질은 코딩테스트를 칠 때는 몰라도 무관.
연결리스트의 종류
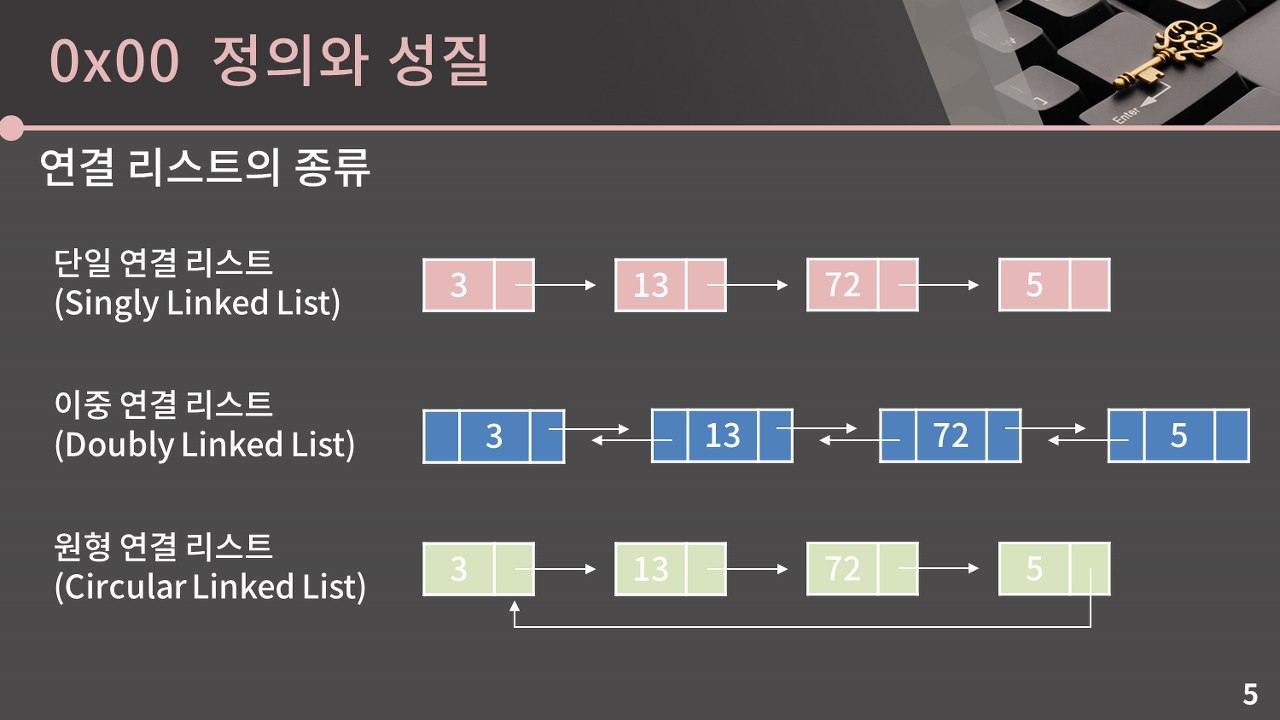
단일 연결 리스트
단일 연결 리스트는 각 원소가 자신의 다음 원소의 주소를 들고 있는 연결 리스트입니다. 자신의 이전 원소는 알 수 없음!
이중 연결 리스트
이중 연결 리스트에서는 하나의 원소에서 해당 원소의 이전과 다음 원소의 주소를 알 수 있다. 다만 원소가 가지고 있어야 하는 정보가 1개 더 추가되니 메모리를 더 쓴다는 단점 존재. 참고로 STL의 list 구조는 이중 연결 리스트!
원형 연결 리스트
원형 연결 리스트에서는 끝이 처음과 연결되어 있다. 그림의 예시는 단일 연결 리스트로 표현했지만 이중 연결리스트여도 상관없음.
배열과 연결리스트의 차이
배열과 연결 리스트는 메모리 상에 원소를 놓는 방법은 다르다고 해도 어찌됐든 원소들 사이의 선후 관계가 일대일로 정의가 된다. 즉, 원소들 사이에서 첫 번째 원소, 두 번째 원소, … 이런 개념이 존재하기 때문에 배열과 연결리스트는 선형 자료구조에 속한다. (트리, 그래프, 해시 등은 비선형 자료구조의 대표적인 예시)
두 자료구조의 차이와 장단점을 비교해보자.
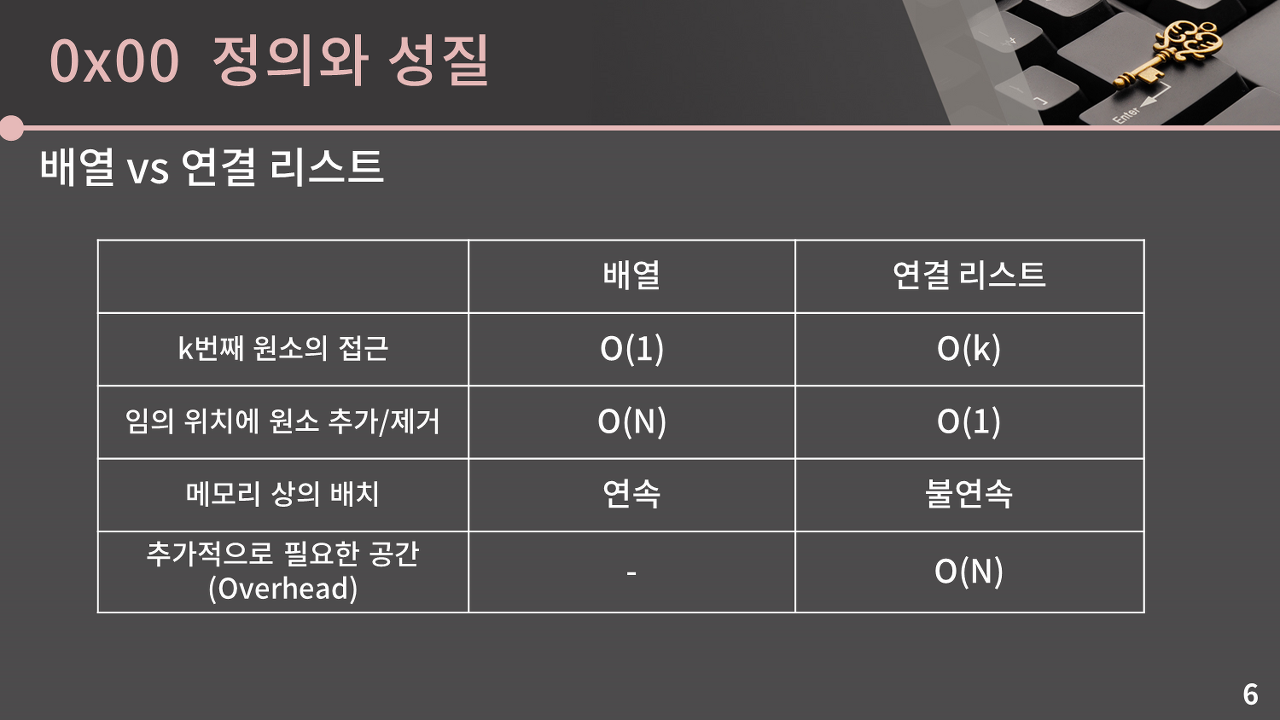
첫 번째로 k번째 원소의 접근은 배열의 경우 O(1), 연결 리스트의 경우 O(k)이다.
두 번째로 임의 위치에 원소를 추가하거나 제거하는건 배열의 경우 O(N), 연결 리스트의 경우 O(1) 이다.
세 번째로 메모리 상의 배치는 배열의 경우 연속, 연결 리스트의 경우 불연속이다.
네 번째로 overhead를 생각해보면 배열은 데이터만 저장하면 되기 때문에 추가적으로 필요한 공간이 없다.
그런데 연결 리스트에서는 각 원소가 다음 원소, 혹은 이전과 다음 원소의 주소값을 가지고 있어야 한다.
그래서 32비트 컴퓨터면 주소값이 32비트(=4바이트) 단위이니 4N 바이트가 추가로 필요하고, 64비트 컴퓨터라면 주소값이 64비트(=8바이트) 단위이니 8N 바이트가 추가로 필요하게 된다. 즉 N에 비례하는 만큼의 메모리를 추가로 쓰인다.
기능과 구현
연결리스트에서의 연산
임의의 위치에 있는 원소 확인/변경하기 O(n)
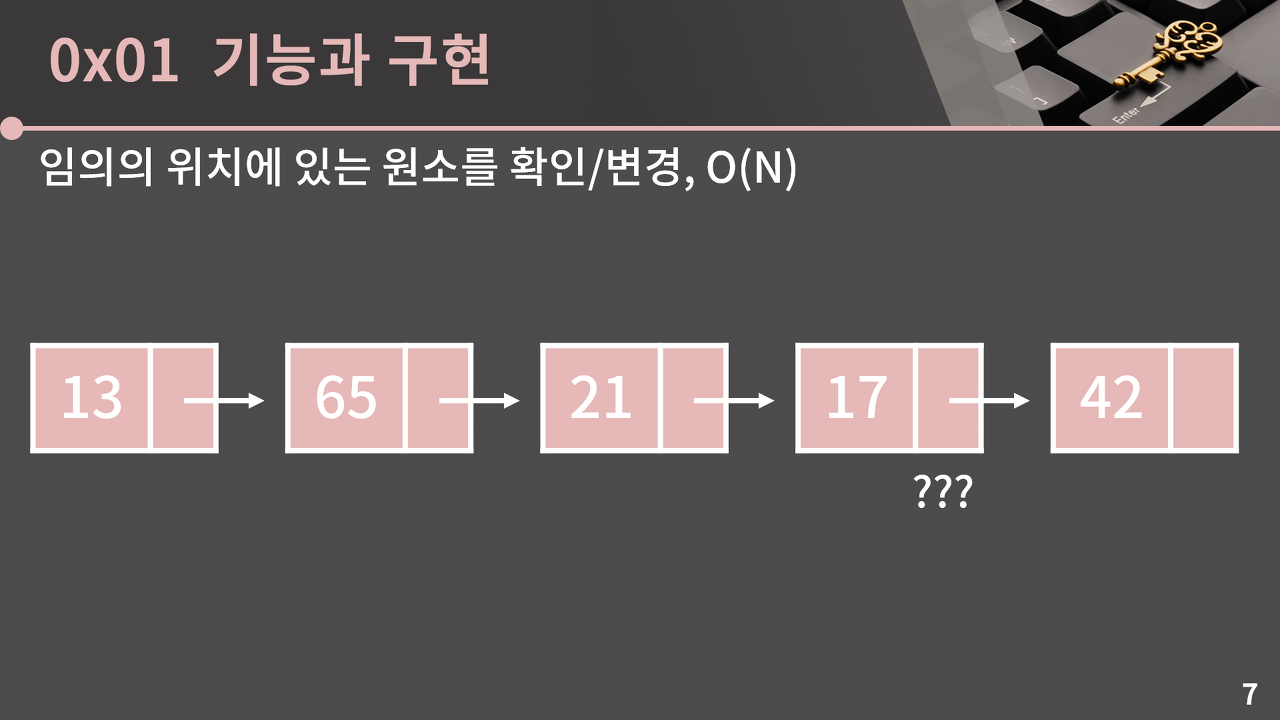
앞서 언급했듯, 배열과는 다르게 임의의 위치에 있는 원소로 가기 위해서는 그 위치에 도달할 때 까지 첫 번째부터 순차적으로 방문을 해야한다.
연결 리스트의 구조 상, 우리는 첫 번째 원소의 주소만 알고 있다. 만약 네 번째 원소의 값을 확인하려 할 때, 우리는 첫 번째 원소에 기록된 주소를 통해 차례대로 네 번째 원소까지 방문해야 한다.
그렇기 때문에 k번째 원소를 보기 위해서는 O(k)의 시간이 필요하고, 전체에 N개의 원소가 있다고 하면 평균적으로 N/2의 시간이 걸리기 때문에 시간복잡도는 O(N)이 된다.
임의의 위치에 원소 추가하기 O(1)
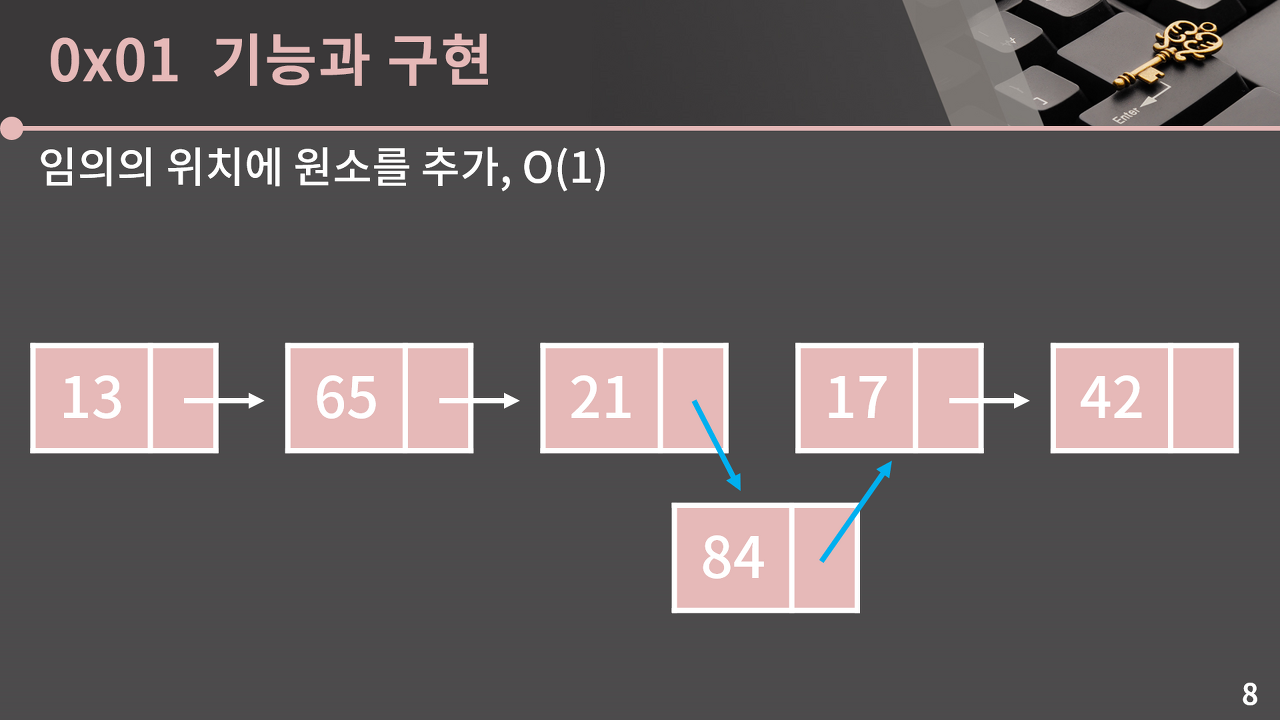
그림과 같은 연결리스트에 값이 84인 원소를 추가하려 한다. 21과 17사이에 추가하기 위해서는 21의 다음 원소를 84로, 17의 이전 원소를 84로 변경하면 가능하기 때문에 배열처럼 나머지 원소를 모두 옮길 필요가 없음!
임의의 위치에 원소 제거하기 O(1)
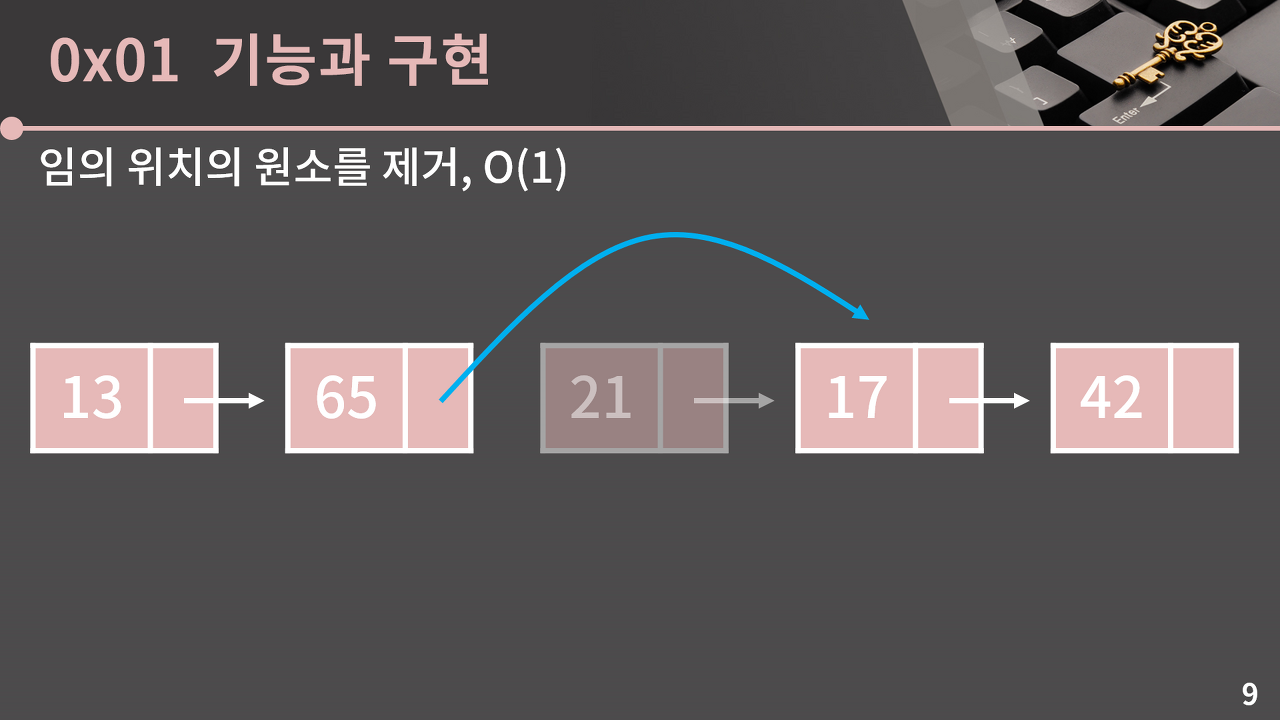
제거도 추가와 마찬가지로 21인 원소를 삭제하기 위해서는 단순히 65의 다음 원소를 17로 변경하면 된다. 물론 메모리 누수를 막기 위해 21 원소의 메모리는 제거할 필요가 있다.
정리

임의의 위치에 있는 원소를 확인하거나 변경하는건 O(N)이고, 해당 위치의 주소를 같이 넘겨줄 때 임의의 위치에 원소를 추가하거나 임의 위치의 원소를 제거하는건 O(1)이다.
배열보다 연결리스트가 유용한 상황은 다음과 같다.
예를 들어 텍스트 에디터에서 커서를 옮기고 글자를 지우는 것과 같은 연산들이 다양하게 주어진 후 최종 결과를 출력하라는 문제에서, 우리는 커서가 가리키는 위치에 글자를 추가하거나 글자를 지우는 명령을 계속 수행해야 한다.
이런 경우에 배열은 임의의 위치에 글자를 추가하는 연산이 비효율적인데, 연결 리스트에서는 O(1)에 처리할 수 있게 된다.
즉 임의의 위치에서 원소를 추가하거나 임의 위치의 원소를 제거하는 연산을 많이 해야 할 경우에는 연결 리스트의 사용을 고려해보면 좋다.
- 연결리스트의 구현은 코드 이해만 하기. 코딩테스트에서는 STL을 이용하자!
STL list
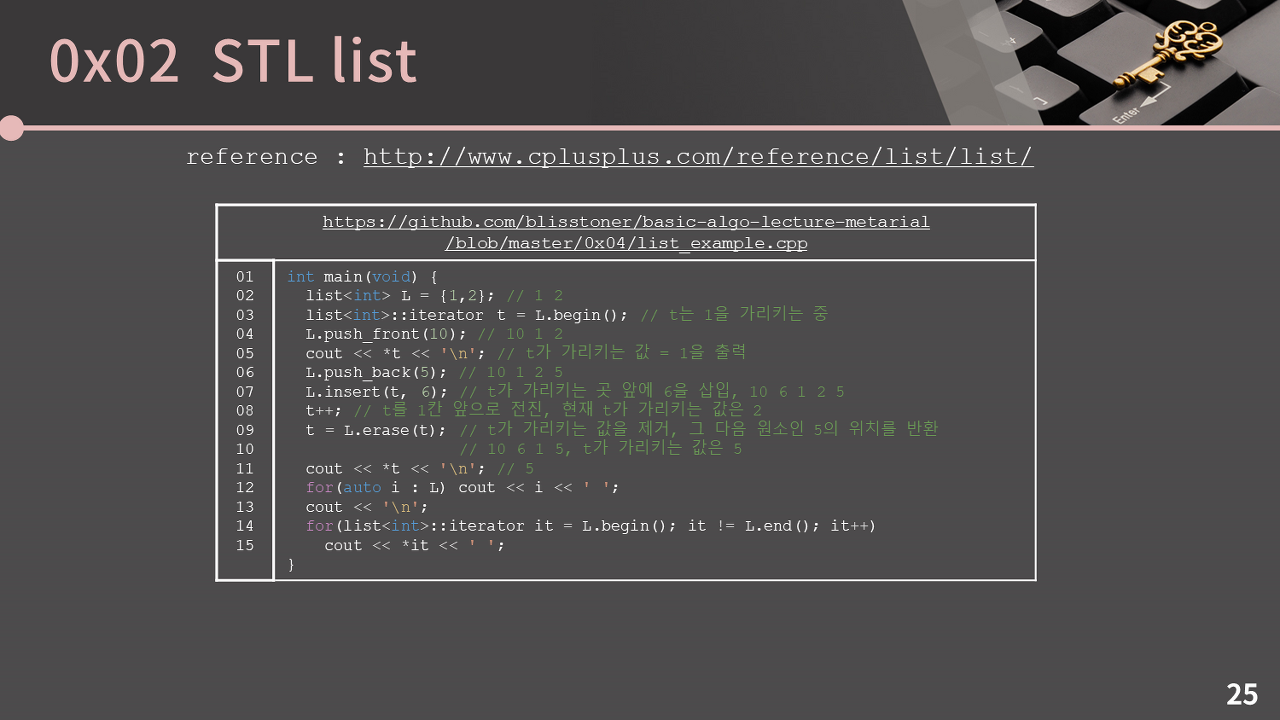
STL을 사용할 수 있는 상황이라면 연결 리스트를 꾸역꾸역 구현하는 것 보다 그냥 STL을 쓰는게 훨씬 더 편하니 STL list의 사용법을 익혀두자.
일단 list에서 push_back, pop_back, push_front, pop_front는 모두 O(1)이고, 여기서는 iterator가 주소 역할을 한다.
3번째 줄에서 list::iterator라는 type을 치기가 귀찮으면 C++11 이상일 때 auto t = L.begin()으로 쓸 수 있음.
erase는 제거한 다음 원소의 위치를 반환한다. 마지막으로 순회를 할 때에는 C++11 이상이라면 12번째 줄과 같이 편하게 할 수 있지만, C++11 미만이라면 14, 15번째 줄과 사용해야한다.
연습문제
백준1406 에디터
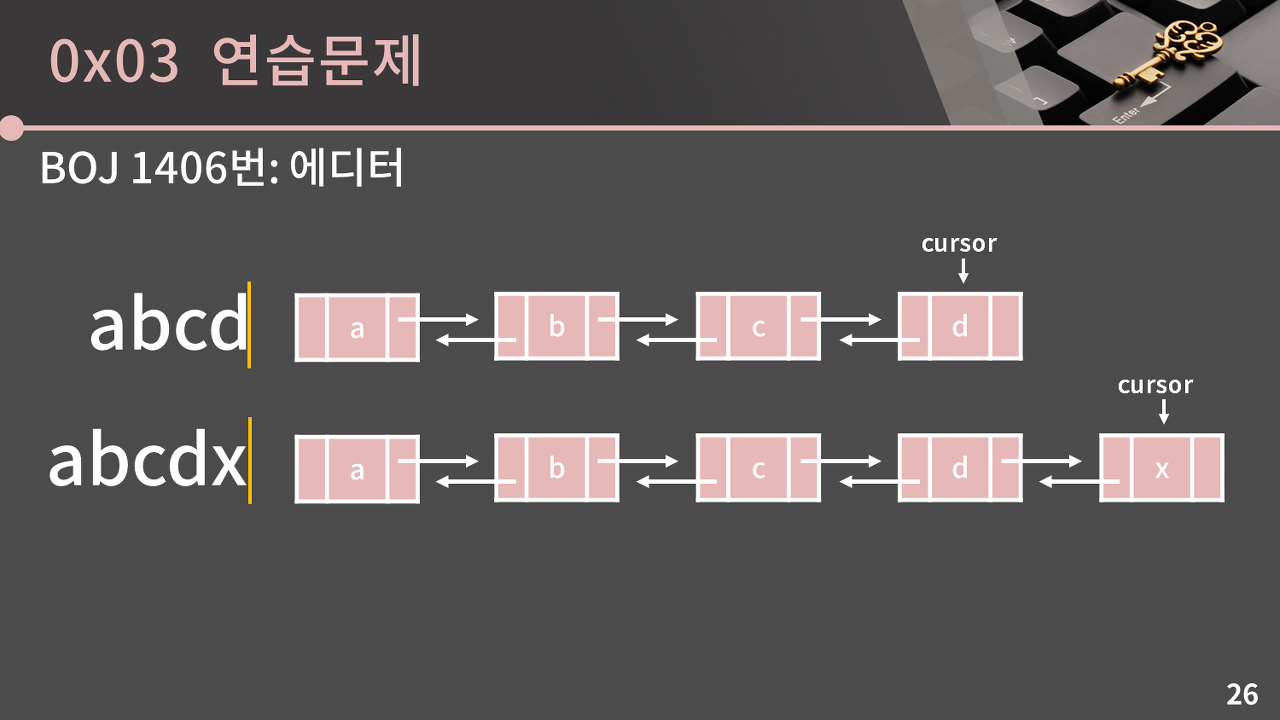
풀이
문제에서는 커서로 표현하며 문자열 abc의 경우, VaVbVcV 4칸에 커서가 존재 할 수 있다. 반면 리스트는 a,b,c의 문자를 가르키기 때문에 예외 처리를 정확히 해주어야 함!!
예를 들어 abcV에서 c문자를 지우는 명령이 일어나면,현재 리스트의 커서는 list.end()를 가르키고 있기 때문에 커서-1을 한 뒤 erase를 해야한다. erase 명령을 실행한 후에는 지워진 문자 다음 원소를 가르키게 되는데, (여기서는 list.end()) 그 값을 다시 커서에 반환해야 한다.

내 코드
#include <iostream>
#include <string>
#include <list>
using namespace std;
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
string str;
char order,c;
list<char> list;
int M;
cin >> str;
for(int j=0; j<str.length(); j++) list.push_back(str[j]);
auto cursor = list.end();
cin >> M;
for(int i=0; i<M; i++){
cin >> order;
if(order == 'L'){
if(cursor != list.begin()) {
cursor--;
}
}
else if(order =='D'){
if(cursor != list.end()) {
cursor++;
}
}
else if(order == 'B'){
if(cursor != list.begin()){
cursor--;
cursor = list.erase(cursor);
}
}
else {
cin >> c;
list.insert(cursor,c);
}
}
for(auto element:list) cout << element;
return 0;
}
삭제(B)에서 list.erase(cursor)를 하면서 반환 된 값을 다시 cursor로 저장 안하는 실수때문에 헤멨다 흑흑
손코딩 문제 1
원형 연결 리스트에서 임의의 노드 하나가 주어졌을 때, 리스트의 길이를 구하는 방법은?
원형 연결 리스트는 순환하기 때문에 임의의 노드를 다시 방문할 때까지 다음 노드로 이동하면 된다. 시간복잡도 O(n), 공간복잡도 O(1)의 효율적인 방법이다.

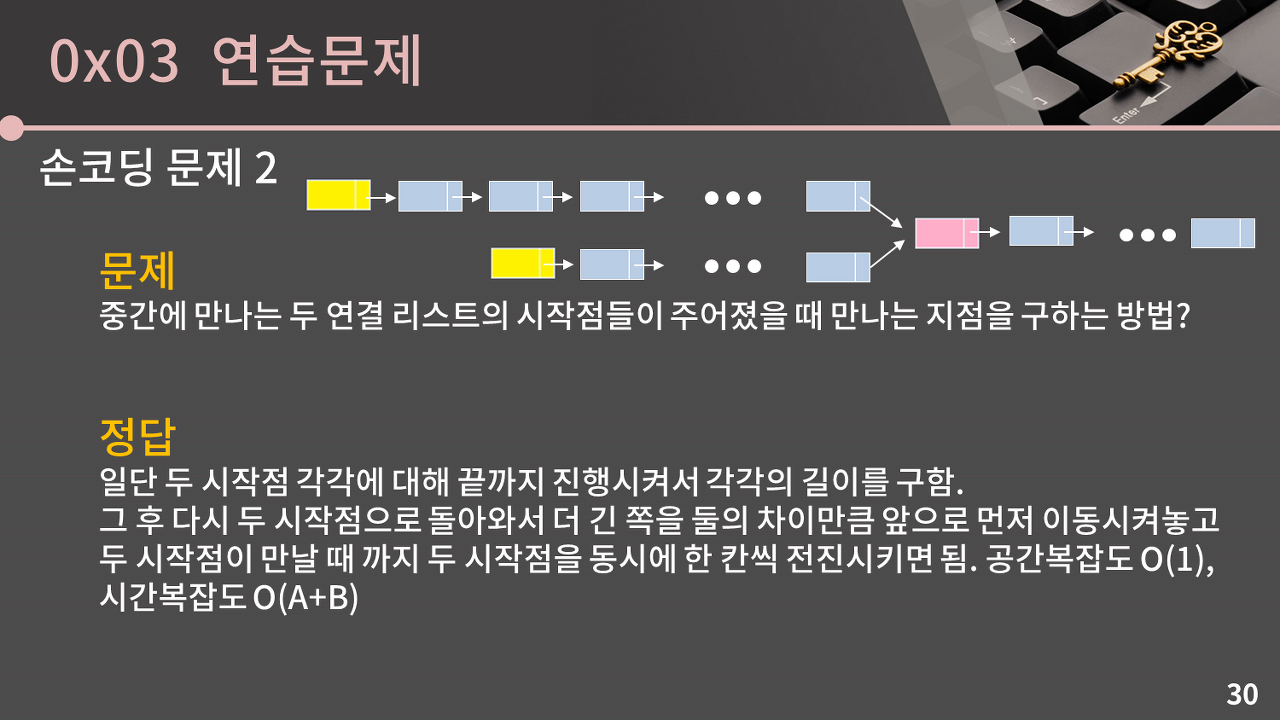
손코딩 문제 2
중간에서 만나는 두 연결 리스트의 시작점들이 주어졌을 때, 만나는 지점을 구하는 방법은?
두 연결리스트의 길이를 먼저 구한 뒤, 그 차이를 알고 있다면 만나는 지점을 구할 수 있다.
둘 중 더 긴 연결리스트를 차이만큼 이동시킨 뒤, 만나는 지점에 도달할 때 까지 두 연결리스트를 동시에 한 칸씩 이동시키면 된다.
손코딩 문제 3
주어진 연결 리스트 안에 사이클이 있는지 판단하여라
Floyd's cycle-finding algorithm 으로 해결이 가능하다.
한 칸씩 가는 커서와 두 칸씩 가는 커서를 동일한 시작점에서 출발시키면 사이클이 있을 경우 두 커서는 반드시 만나게 된다. 반대로 만약 사이클이 없으면 두 커서가 만나지 못하고 연결 리스트의 끝에 도달한다.
이 방식을 이용하면 거치는 모든 노드를 저장할 필요가 없이 공간복잡도 O(1)에 사이클의 존재 여부를 알 수 있다.

