Big-O
알고리즘의 성능을 수학적으로 표현해주는 표기법
- 알고리즘의 시간과 공간 복잡도를 표현함
- Big-O는 알고리즘의 실제 러닝타임을 표시하는 것이 아닌, 데이터나 사용자의 증가율에 따른 알고리즘의 성능을 예측하는 것이 목표임
O(1)
constant time
입력 데이터의 크기에 상관없이 언제나 일정한 시간이 걸리는 알고리즘
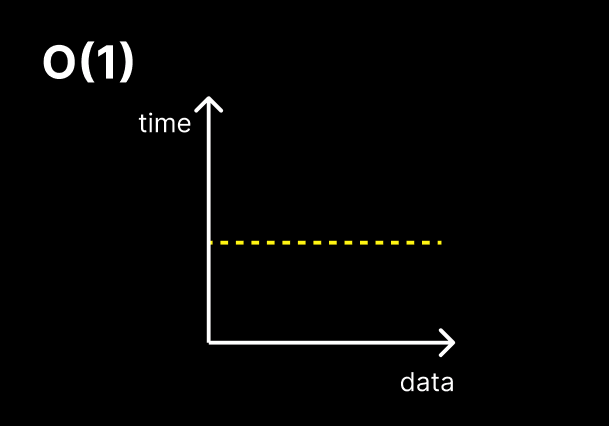
데이터가 증가함에 따라 성능(처리시간)에 변함이 없다.
O(n)
liner time
입력 데이터의 크기에 비례한 처리 시간이 걸리는 알고리즘
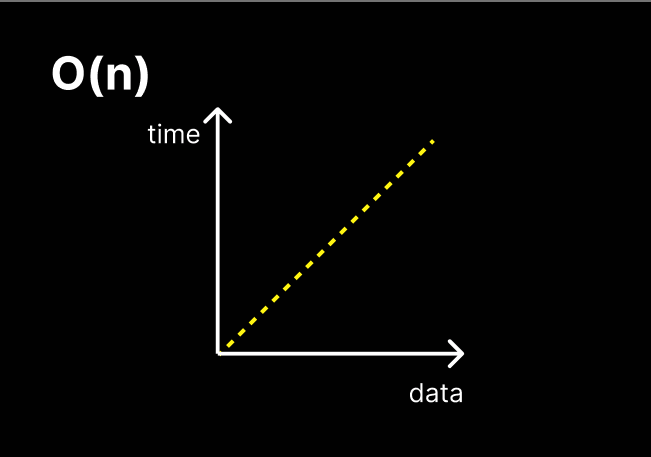
언제나 데이터와 처리시간이 같은 비율로 증가
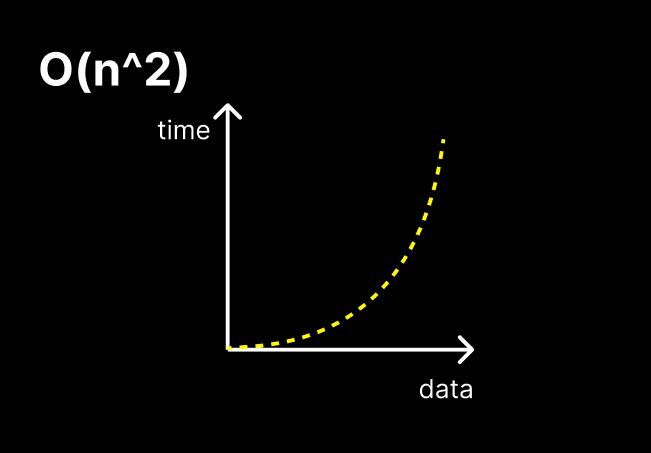
O(n^2)
quadratic time
데이터가 증가함에 따라 처리 시간의 부담에 가속도가 붙는다.
for(let i=0; i<n; i++) {
for(let j=0; j<n; j++) {
...
}
}
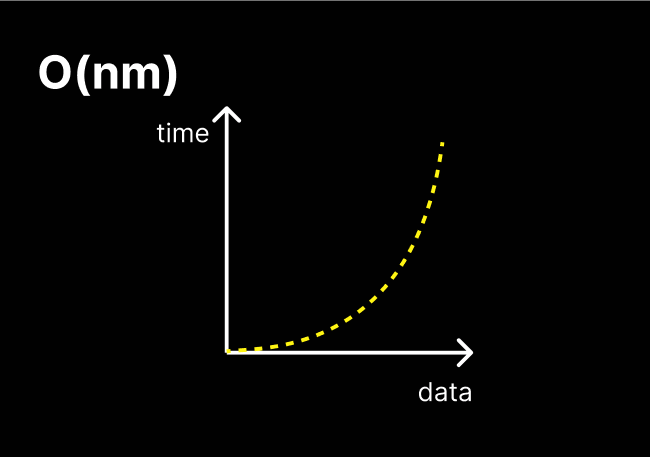
O(nm)
quadratic time
데이터가 증가함에 따라 처리 시간의 부담에 가속도가 붙는다.
단, 변수가 다르다는 점에서 O(n^2)과 차이가 있다.
for(let i=0; i<n; i++) {
for(let j=0; j<m; j++) {
...
}
}
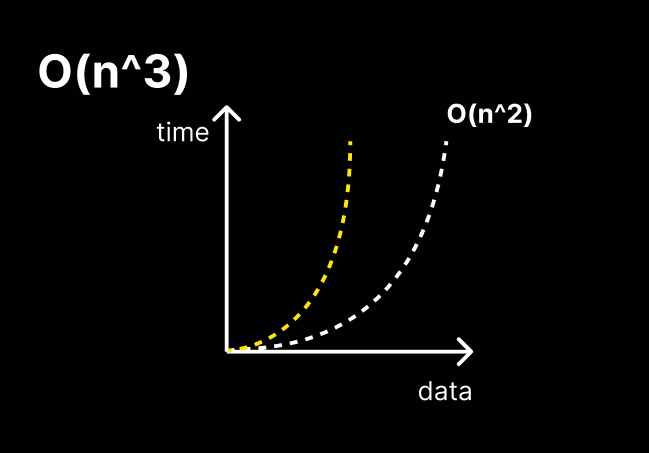
O(n^3)
polynomail / cubic time
데이터가 증가함에 따라 처리 시간이 더 급격하게 늘어난다.
for(let i=0; i<n; i++) {
for(let j=0; j<n; j++) {
for(let k=0; k<n; k++) {
...
}
}
}
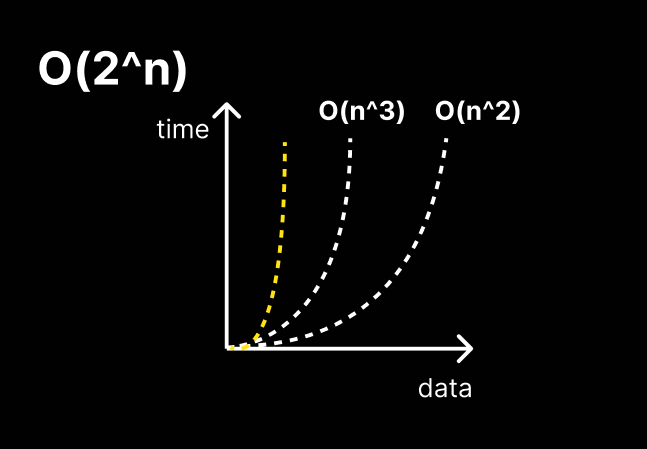
O(2^n)
exponential time
대표적인 예시로 Fibonacci 수열이 있다.
const Fibonacci = (n) => {
if(n<=1) return n
return Fibonacci(n-1) + Fibonacci(n-2)
}함수가 호출될 때마다 두번씩 함수가 호출됨
데이터가 증가함에 따라 처리 시간이 현저하게 늘어남.
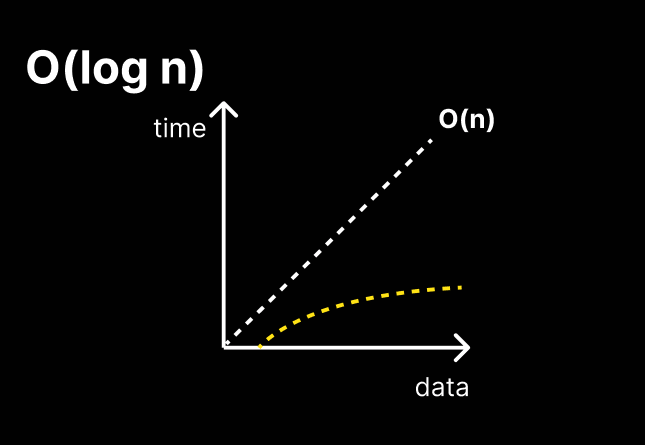
O(log n)
대표적인 예시로 binary search(이진탐색)이 있다.
데이터 처리가 진행될 때마다 검색해야 하는 데이터의 양이 절반씩 떨어지는 알고리즘
순차 검색에 비해 속도가 훨씬 빠르다.