[Algorithm] 에라토스테네스의 체

[ 오늘의 주제는? ]

알고리즘 문제를 풀 때 가끔 소수 판별을 구현해야 할 때가 있는데 매번 까먹어서 제대로 정리해보려고 한다.

[ 에라토스테네스의 체란? ]

여러 개의 수가 소수인지 아닌지를 판별할 때 사용하는 대표적인 알고리즘.
N보다 작거나 같은 모든 소수를 찾을 때 사용할 수 있다.

• 소수란? 1과 자기 자신 외의 약수를 가지지 않는 1보다 큰 자연수를 말한다.

1. 동작 과정

에라토스테네스의 체의 과정은 다음과 같다.

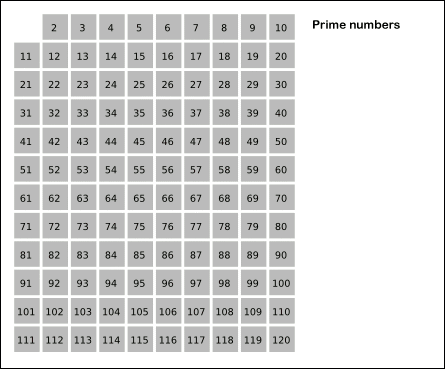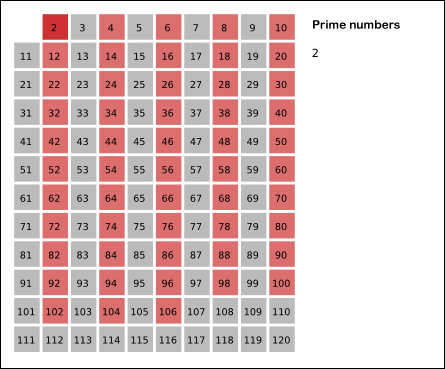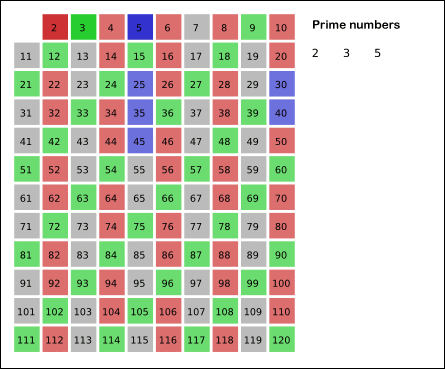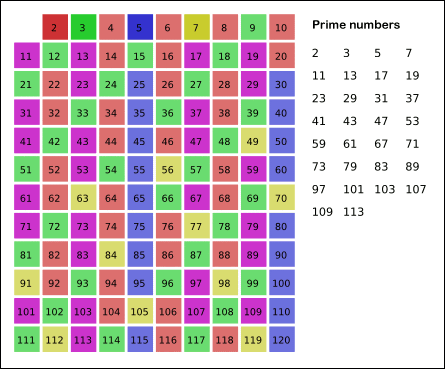
1. 2부터 N까지의 모든 자연수를 나열한다.
2. 남은 수 중에서 아직 처리하지 않은 가장 작은 수 i를 찾는다.
3. 남은 수 중에서 i의 배수를 모두 제거한다. (i는 제거하지 않는다.)
4. 더 이상 반복할 수 없을 때까지 2번과 3번 과정을 반복한다.

🔼 이미지 출처 - 위키백과

2. 장단점

에라토스테네스의 체 알고리즘의 시간 복잡도는 O(NloglogN)으로 사실상 선형 시간에 동작할 정도로 빠르다. 그래서 다수의 소수를 찾아야 하는 문제에서 자주 사용된다.

하지만 알고리즘을 수행할 때 N의 크기만큼 리스트를 할당해야 하기 때문에 메모리가 많이 필요하다는 단점이 있다. 또한 10억이 소수인지 찾아야 하는 문제에서는 에라토스테네스의 체를 이용하기 어렵다.

[ 코드 ]

import math

n = 1000    # 2부터 1,000까지의 모든 수에 대하여 소수 판별
array = [True for i in range(n + 1)]    # 처음에는 모든 수가 소수(True)인 것으로 초기화 (0과 1은 제외)

# scores 알고리즘
for i in range(2, int(math.sqrt(n)) + 1):   # 2부터 n의 제곱근까지의 모든 수를 확인하며
    if array[i]:                            # i가 소수인 경우 (남은 수인 경우)
        for j in range(i + i, n, i):        # i의 배수 모두 False로 변환
            array[j] = False

# 모든 소수 출력
for i in range(2, n + 1):
    if array[i]:
        print(i, end=' ')

출력 결과

2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199 211 223 227 229 233 239 241 251 257 263 269 271 277 281 283 293 307 311 313 317 331 337 347 349 353 359 367 373 379 383 389 397 401 409 419 421 431 433 439 443 449 457 461 463 467 479 487 491 499 503 509 521 523 541 547 557 563 569 571 577 587 593 599 601 607 613 617 619 631 641 643 647 653 659 661 673 677 683 691 701 709 719 727 733 739 743 751 757 761 769 773 787 797 809 811 821 823 827 829 839 853 857 859 863 877 881 883 887 907 911 919 929 937 941 947 953 967 971 977 983 991 997 

[ 📘 Reference ]

이것이 코딩테스트다 with 파이썬 책