manacher 알고리즘

🔍manacher 알고리즘이란

• 문자열 내 palindrome(회문)을 찾는데 활용되는 알고리즘
• palindrome의 대칭성을 이용해 다음 탐색 시 이전에 탐색한 구간의 정보를 활용
• 시간복잡도: O(n)

⚙️동작원리

사전 정의

S: 문자열
A : 'S[i]를 중심으로 하는 가장 긴 palindrome 반지름 길이'의 배열
i : 배열의 index, 0 <= i <= |S| - 1
j : 이전 index, j < i
R : 모든 j의 palindrome 범위 중 가장 멀리 떨어진 index, R = max(j+A[j])
p : R의 중점, R = max(j+A[j]) = p+A[p]
i': p를 중심으로 둔 i의 대칭점

알고리즘

1. i는 0부터 |S| - 1까지 오름차순으로 진행
2. i <= R 여부에 따라 A[i]의 초기값 설정
   • i > R인 경우, i가 p의 palindrome에 속하지 않으니 A[i]의 초기값은 0
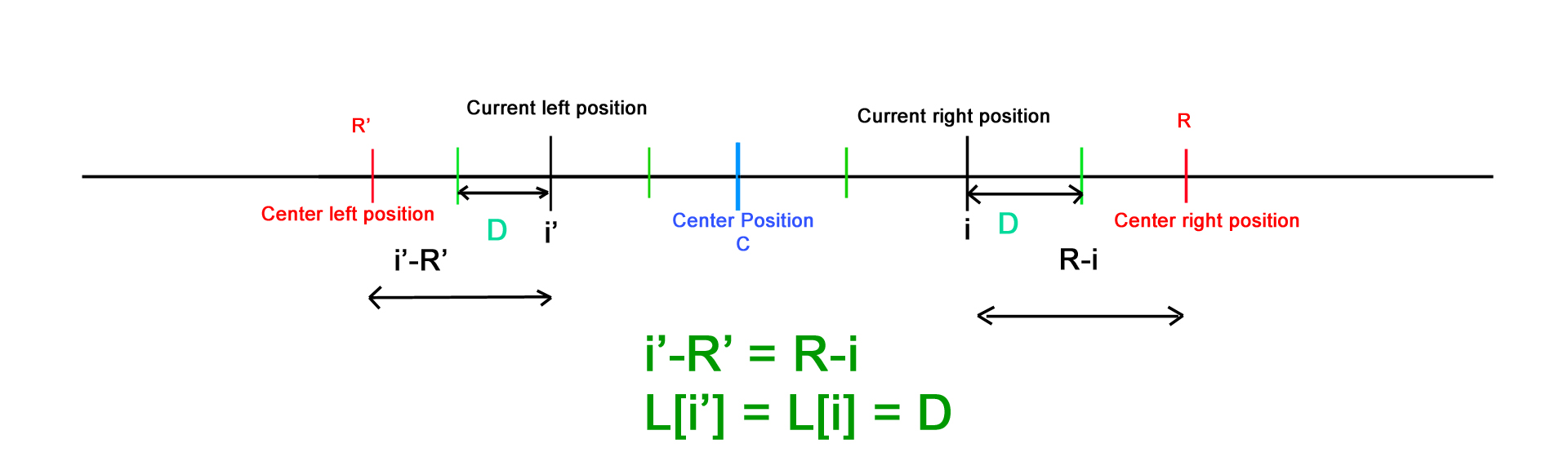
   • i <= R이면서 A[i'] <= R - i인 경우, i를 기준으로 반지름이 A[i']인 문자열을 Si라 할 때 Si는 p가 중점인 palindrome에 속하므로 대칭성을 만족,
     [S[i'-A[i'], S[i'+A[i']] 문자열과 동일하기에 palindrome을 형성
   • 반면, A[i'] > R + i인 경우 기존 palindrome을 벗어나기에 R부터 한칸 씩 늘려가며 탐색하는 과정이 필요
   • 즉 A[i]의 초기값은 min(R-i, A[i'])
3. A[i]의 초기값에서부터 S[i - A[i]]와 S[i + A[i]]가 같다면 palindrome을 형성하므로 A[i]를 증가시키고, 아니라면 그 다음 i로 넘어간다.

💻구현

BOJ 13275

#include <bits/stdc++.h>
#define MAX 1000001

using namespace std;



string str = "", tmp;
int p=0, R=0, N, ans=0;
int A[MAX];



void manacher(string str){
    N = str.size();
    for(int i=0; i<N; i++){

        int ii = 2*p - i; // p를 기준으로 한 i의 대칭점

        if(i > R) A[i] = 0;
        else A[i] = min(R-i, A[ii]);


        while(i - A[i] -1 >= 0 && i + A[i] +1 < N && str[i-A[i]-1] == str[i+A[i]+1]) A[i]++;
        // A[i] 탐색



        if(R < i + A[i]){
            p = i;
            R = i+A[i];
        }//R 업데이트

        ans = max(ans, A[i]); // ans 업데이트

    }

    return ;
}
int main()
{

    cin >> tmp;

    N = tmp.size();


    for(int i=0; i < N; i++){
        str += '#';
        str += tmp[i];
    }
    str += '#';

    // string 사이에 '#'을 삽입해 기준점이 없는 palin(N이 짝수인 str)에 인위적으로 기준점을 만들어줌


    manacher(str);

    cout << ans;

    return 0;
}

참고자료

대표 이미지 출처