관계 데이터 연산

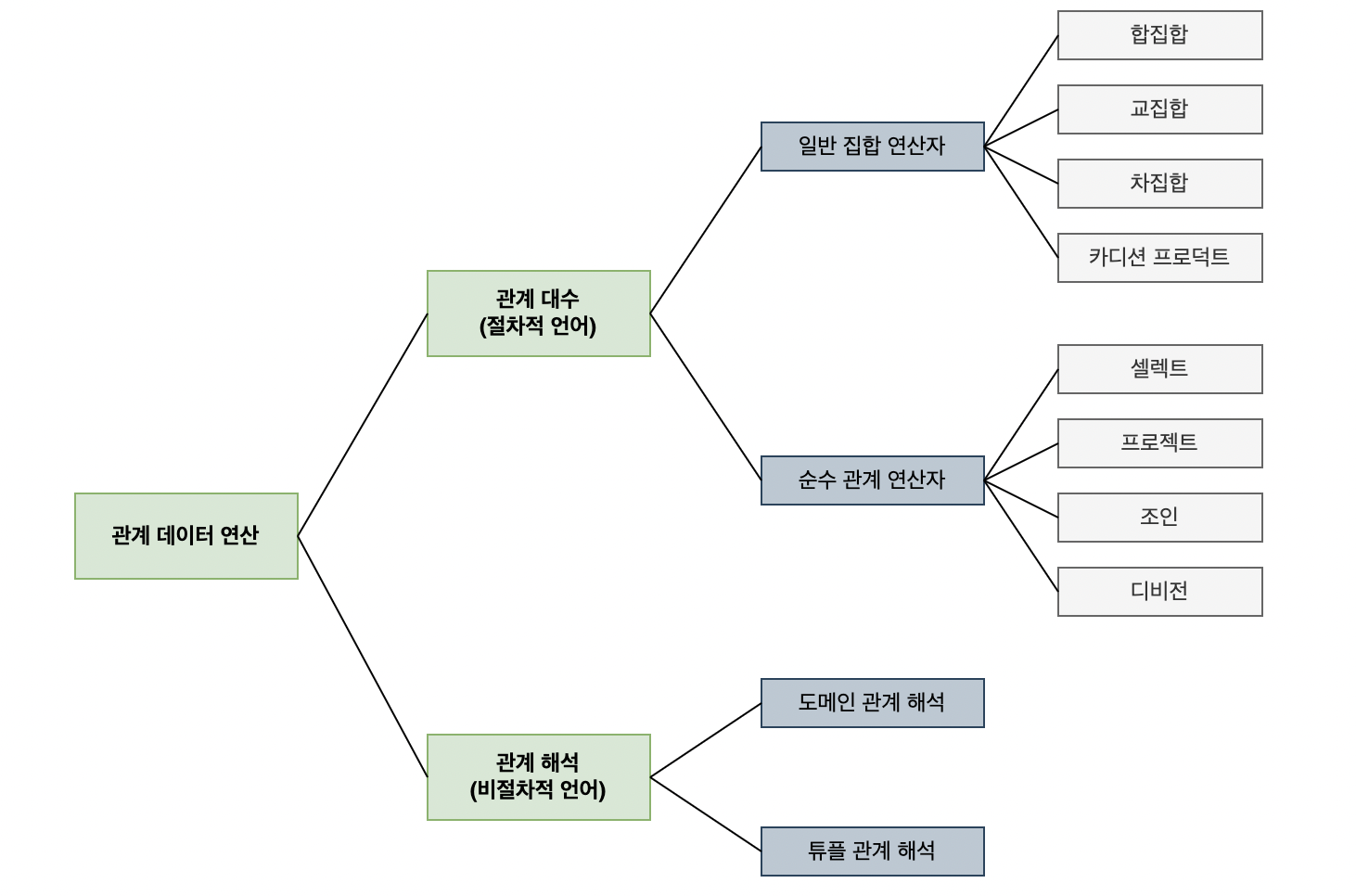
🔗 관계 데이터 연산(relational data operation)

• 관계 데이터 모델의 연산
• 원하는 데이터를 얻기 위해 릴레이션에 필요한 처리 요구를 수행하는 것
• 관계 대수와 관계 해석이 있습니다.
  • 기능과 표현력 측면에서 능력이 동등합니다.
  • 처리 절차를 얼마나 자세히 기술하느냐에 따라 차이를 보입니다.

🥽 관계 대수(relational algebra)의 개념

• 원하는 결과를 얻기 위해 릴레이션의 처리 과정을 순서대로 기술하는 언어
  • 절차 언어(procedural language)
• 릴레이션을 처리하는 연산자들의 모임
  • 대표 연산자 8개
  • 일반 집합 연산자와 순수 관계 연산자로 분류됩니다.
• 폐쇄 특성(closure property)이 존재합니다.
  • 피연산자도 릴레이션이고 연산의 결과도 릴레이션입니다.

🛠️ 일반 집합 연산자(set operation)

• 릴레이션이 튜플의 집합이라는 개념을 이용하는 연산자
  

🧩 순수 관계 연산자(relational operation)

• 릴레이션의 구조와 특성을 이용하는 연산자
  

💎 일반 집합 연산자의 특성

• 피연산자가 두 개 필요합니다.
  • 두 개의 릴레이션을 대상으로 연산을 수행
• 합집합, 교집합, 차집합은 피연산자인 두 릴레이션이 합병이 가능해야 합니다.
  • 합병 가능(union-compatible) 조건
    • 두 릴레이션의 차수가 같아야 합니다.
    • 두 릴레이션에서 서로 대응되는 속성의 도메인이 같아야 합니다.

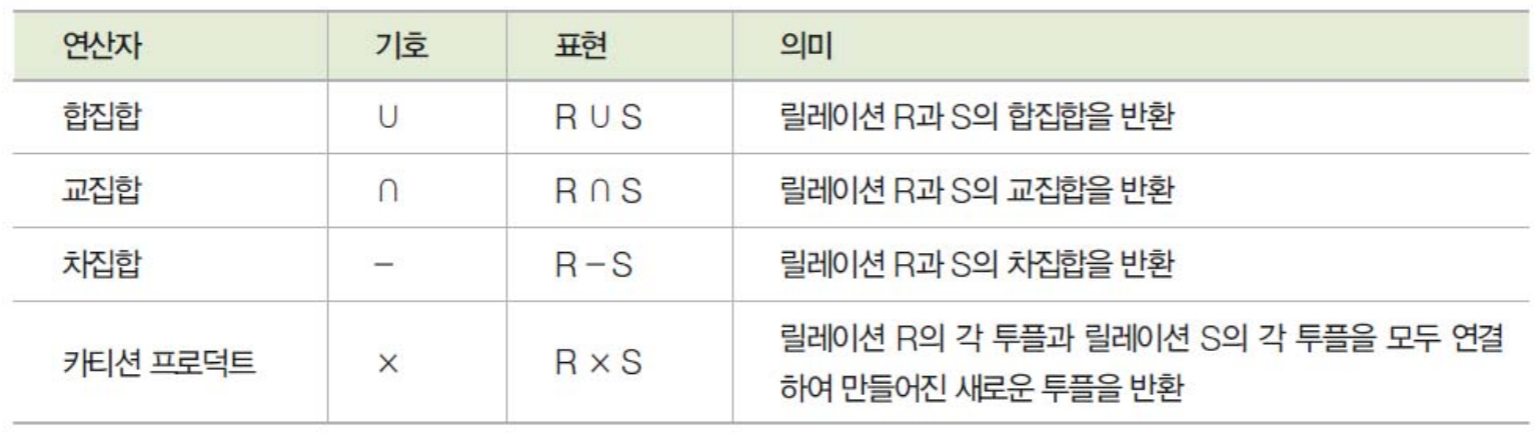
➕ 일반 집합 연산자 - 합집합(union)

• 합병 가능한 두 릴레이션 R과 S의 합집합
  • 릴레이션 R에 속하거나 릴레이션 S에 속하는 모든 튜플로 결과 릴레이션을 구성
• 결과 릴레이션의 특성
  • 차수는 릴레이션 R과 S의 차수와 같습니다.
  • 카디널리티는 릴레이션 R과 S의 카디널리티를 더한 것과 같거나 적어집니다.
• 교환적 특징이 있습니다.
  • R$U$S = S$U$R
• 결합적 특징이 있습니다.
  • (R$U$S) $U$ T = R$U$(S$U$T)

🪢 일반 집합 연산자 - 교집합(intersection)

• 합병 가능한 두 릴레이션 R과 S의 교집합: R$∩$S
  • 릴레이션 R과 릴레이션 S에 속하는 모든 튜플로 결과 릴레이션 구성
• 결과 릴레이션의 특성
  • 차수 릴레이션 R과 S의 차수와 같습니다.
  • 카디널리티는 릴레이션 R과 S의 어떤 카디널리티보다 크지 않습니다.
• 교환적 특징이 있습니다.
  • R∩S = S∩P
• 결합적 특징이 있습니다.
  • (R∩S)∩T = R∩(S∩T)

➖ 일반 집합 연산자 - 차집합(difference)

• 합병 가능한 두 릴레이션 R과 S의 차집합: R-S
  • 릴레이션 R에는 존재하고 릴레이션 S에는 존재하지 않는 튜플로 결과 리레이션을 구성
• 결과 릴레이션의 특성
  • 차수는 릴레이션 R과 S의 차수와 같습니다.
  • R-S의 카디널리티는 릴레이션 R의 카디널리티와 같거나 적습니다.
  • S-R의 카디널리티는 릴레이션 S의 카디널리티와 같거나 적습니다.
• 교환적, 결합적 특징이 없습니다.

✖️ 일반 집합 연산자 - 카디션 프로덕트(cartesian product)

• 두 릴레이션 R과 S의 카티션 프로덕트: RXS
  • 릴레이션 R에 속한 각 튜플과 릴레이션 S에 속한 각 튜플을 모두 연결하여 만들어진 새로운 튜플로 결과 릴레이션을 구성
• 결과 릴레이션의 특성
  • 차수는 릴레이션 R과 S의 차수를 더한 것과 같습니다.
  • 카디널리티는 릴레이션 R과 S의 카디널리티를 곱한 것과 같습니다.
• 교환적 특징이 있습니다.
  • RxS = SxR
• 결합적 특징이 있습니다.
  • (RxS)xT = Rx(SxT)

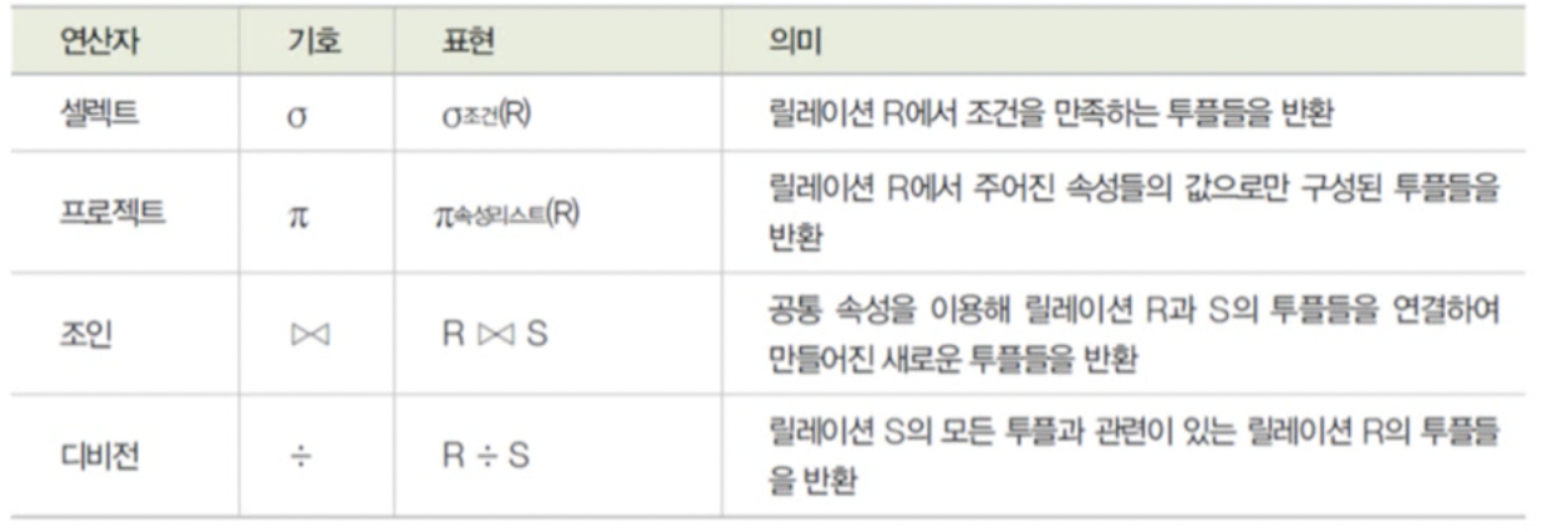
👈 순수 관계 연산자 - 셀렉트(select)

• 릴레이션에서 조건을 만족하는 튜플만 선택하여 결과 릴레이션을 구성
• 하나의 릴레이션을 대상으로 연산을 수행
• 수학적 표현법: σ(릴레이션)
• 데이터 언어적 표현법: 릴레이션 where 조건식
• 조건식
  • 비교식, 프레디킷(predicate)이라고도 합니다.
  • 속성과 상수의 비교나 속성들 간의 비교로 표현합니다.
  • 비교 연산자(>,<,>=...)와 논리 연산자(∧(and) ∨(or) ￢(not))를 이용해 작성합니다.
• 교환적 특징이 있습니다.

🥧 순수 관계 연산자 - 프로젝트(project)

• 릴레이션에서 속성(attribution)에 속한 열을 추출하여 새로운 릴레이션을 생성합니다.
• 표현법: $π_a$(릴레이션)

🕹️ 순수 관계 연산자 - 조인(join)

• 조인 속성을 이용해 두 릴레이션을 조합하여 결과 릴레이션을 구성
  • 조인 속성의 값이 같은 튜플만 연결하여 생성된 튜플을 결과 릴레이션에 포함
  • 조인 속성: 두 릴레이션이 공통으로 가지고 있는 속성
• 표현법: 릴레이션1 ⋈ 릴레이션2
• 자연 조인(natural join)이라고도 합니다.
  • 표현법: 릴레이션1 $⋈_N$ 릴레이션2
• 동일한 조인 속성을 가진 값이 없는 경우는 결과 값에 반영하지 않습니다.

➗ 순수 관계 연산자 - 디비전(division)

• 표현법: 릴레이션1 ÷ 릴레이션2
• 릴레이션2의 모든 튜플과 관련이 있는 릴레이션1의 튜플로 결과 릴레이션을 구성
  • 단, 릴레이션1이 릴레이션2의 모든 속성을 포함하고 있어야 연산이 가능합니다.

📚 참고자료

관련 강의 - 데이터베이스의 원리와 응용(KOCW) 10강
관련 블로그 - 순수 관계 연산자