투 포인터 (BOJ 1644 소수의 연속합)

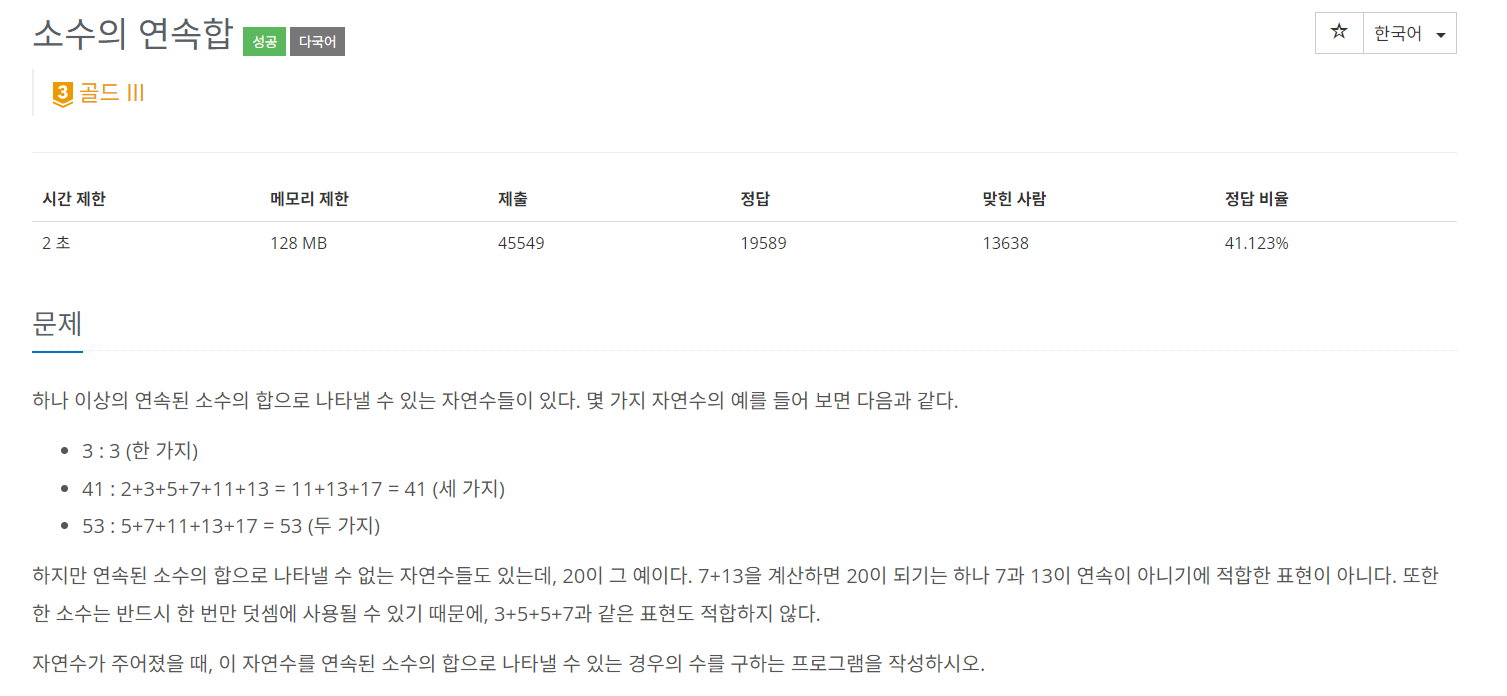
문제

소수의 연속합

에라토스테네스의 체

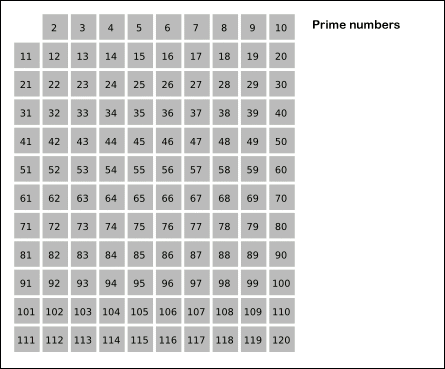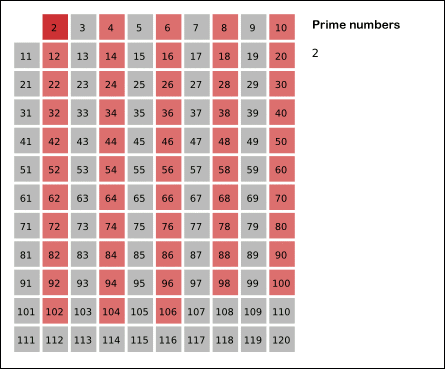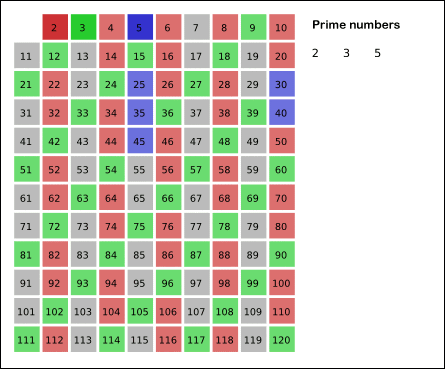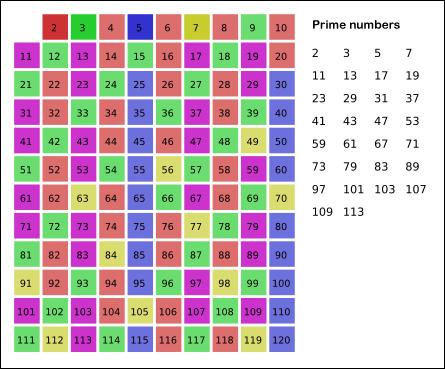
소수를 찾는 빠르고 쉬운 방법
고대 그리스의 수학자 에라토스테네스가 발견

알고리즘

1. 2부터 소수를 구하고자 하는 구간의 모든 수를 나열
2. 나열한 수를 순차적으로 탐색하며 자신을 제외한 배수를 모두 지움
3. 2의 과정에서 탐색된 수는 더이상 탐색 x
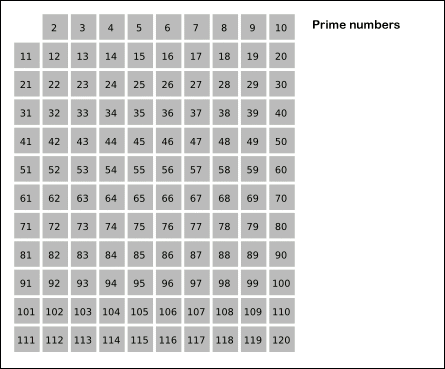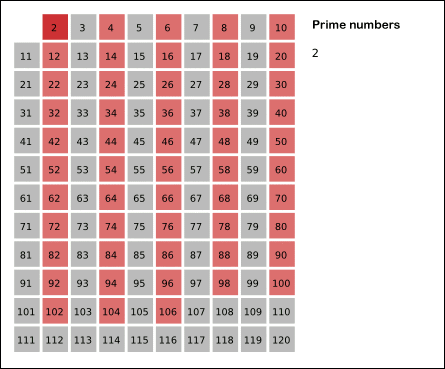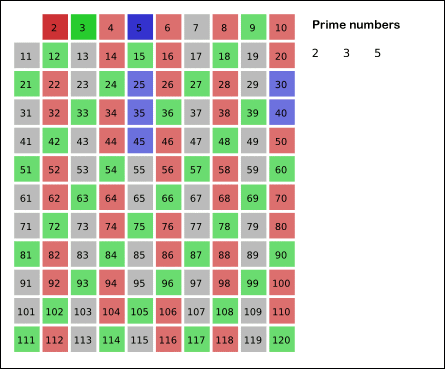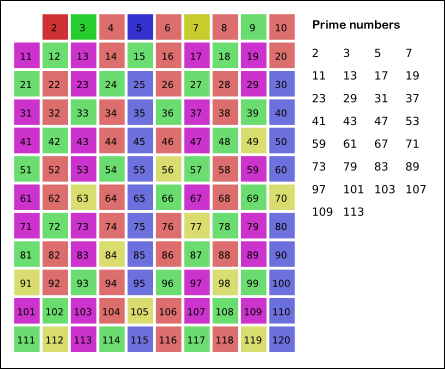
4. 2~3 과정을 반복하면 소수만 남게 됨

풀이

1. 에라토스테네스의 체로 N 이하인 소수들의 배열을 생성
2. 해당 배열을 기준으로 투포인터를 활용해 연속합을 구함
   2-1. low와 high는 0에서 출발
   2-2. 구간합이 N보다 크다면 low를 증가 (구간합 감소)
   2-3. 구간합이 N보다 작다면 high를 증가 (구간합 증가)
   2-4. 구간합이 N과 같다면 ret++
   2-5. high가 끝점에 도달하면 탐색을 종료

코드

#include<bits/stdc++.h>

using namespace std;

int N, ret = 0, pidx = 0, low = 0, high = 0, sum = 0;
int che[4000004] = {0,};
int prime[4000004] = {0,};


void era(int maxNum){
	for(int i=2; i <= maxNum; i++){
		if(che[i]) continue;
		
		for(int j = 2*i; j<=maxNum; j+=i){
			che[j] = 1;
		} // i의 배수들은 소수가 아니므로 모두 1로 표시 
	} // che[i]  == 0이라면 소수 
}

void run(){
	cin >> N;
	
	if(N == 1){
		cout << 0;
		return;
	}

	era(N);
	
	for(int i=2; i<=N; i++){
		if(!che[i]) prime[pidx++] = i;
	}
	
	while(true){
		if(sum >= N) sum -= prime[low++]; // 구간합이 N보다 크다면 low 증가(구간합 감소) 
		else if(high == pidx) break; // high가 0에서 출발해 끝점에 도달하면 break 
		else sum += prime[high++]; // 구간합이 N보다 작다면 high 증가(구간합 증가) 
		if(sum == N) ret++; // 구간합이 N과 같다면 ret++ 
	}
	
	cout << ret;
	
}

int main(){
	run();
	return 0;
}

후기

알고리즘 공부를 시작하며 처음 풀어본 투포인터.

그리디, 완탐, DP에 익숙해진 상태라 그런지
처음 문제를 마주했을 때 어떤 식으로 풀어야할지 막막했던 기억..

소수 판별부터 시간 복잡도를 너무 써서 시간초과의 압박만 받다가
결국 투포인터와 에라토스테네스의 체를 학습한 후 풀어냄.

배워야할게 많다. 나 진짜 많이 놀았구나