[백준] 1260번: DFS와 BFS

💡 문제 설명

정점의 개수와 간선의 개수, 그리고 시작 정점 번호를 첫 줄에 입력으로 주고, 그 다음 간선의 개수에 해당하는 줄만큼 간선이 연결된 두 정점의 번호가 입력으로 주어진다.

이후 깊이우선탐색(depth first search)와 너비우선탐색(breadth first search)에 따라 정점을 방문하여, 방문한 순서대로 정점의 번호를 출력하는 문제다.

DFS와 BFS의 개념을 알았다면, 이를 코드로 구현해보는 연습을 할 수 있는 전형적인 문제였다.

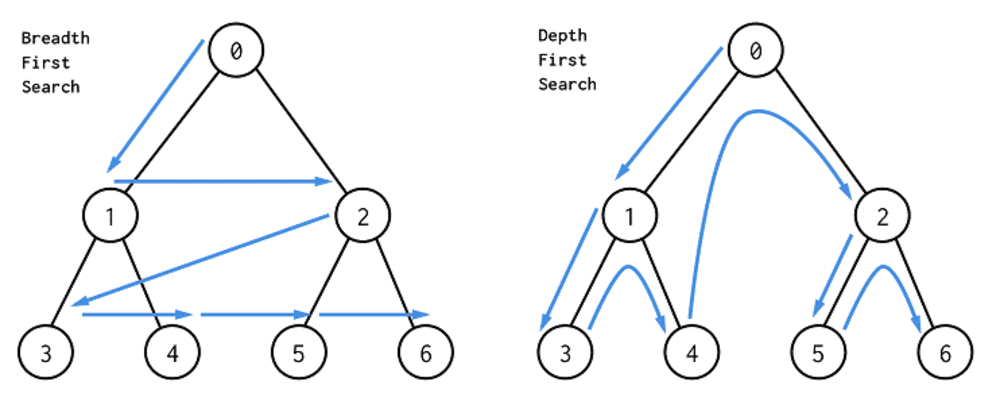
아래의 사진은 DFS와 BFS의 개념을 한눈에 볼 수 있는 시각적 이미지.

✍️ 풀이 및 코드

사실 알고리즘의 개념 자체는 어렵지 않다. 다만 알고리즘 코딩에 익숙지 않다면(나의 경우는 그랬다), 그래프를 어떤 자료형으로 구현해야할지 감이 잘 잡히지 않을 수 있다.

먼저 그래프 자체는 인접행렬(Adjacency array)과 인접리스트(Adjacency list) 두 방법이 있는데 다음의 방법은 인접리스트를 통해 만들었다.

graph = [[] for _ in range(N+1)] # 인덱스가 각 노드의 번호를 지칭

for _ in range(M):
    a,b  = map(int, input().split())
    graph[a].append(b)
    graph[b].append(a) # 양방향 그래프

일반적으로는 dfs는 재귀(Recursive)를 통해 구현하거나, 또는 스택(Stack) 자료형을 통해 구현한다. 각 방법은 장단점이 있다. bfs는 일반적으로 큐(Queue) 자료형을 통해 구현한다.

나의 경우는 dfs는 코드의 간결성을 위해 재귀를 사용했고 bfs는 collections.deque를 통한 Queue로 구현했다.

def dfs(start):
    
    visited[start] = 1
    print(start, end=" ")

    for i in graph[start]:
        if visited[i] == 0:
            dfs(i)
    

def bfs(start):
    queue = deque([start])
    visited[start] = 1

    while queue:
        v = queue.popleft()
        print(v, end=" ")

        for i in graph[v]:
            if visited[i] == 0:
                queue.append(i)
                visited[i] = 1

이 때 변수 'visited'를 통해 해당 정점이 이미 방문한 곳인지, 아닌지를 판단한다.

다음은 전체 코드이다.

import sys
input = sys.stdin.readline
from collections import deque, defaultdict

N, M, V = map(int, input().split())
graph = [[] for _ in range(N+1)] # 인덱스가 각 노드의 번호를 지칭

for _ in range(M):
    a,b  = map(int, input().split())
    graph[a].append(b)
    graph[b].append(a) # 양방향 그래프

for i in graph:
    i.sort()


def dfs(start):
    
    visited[start] = 1
    print(start, end=" ")

    for i in graph[start]:
        if visited[i] == 0:
            dfs(i)
    

def bfs(start):
    queue = deque([start])
    visited[start] = 1

    while queue:
        v = queue.popleft()
        print(v, end=" ")

        for i in graph[v]:
            if visited[i] == 0:
                queue.append(i)
                visited[i] = 1

visited = defaultdict(int)
dfs(V)
print()

visited = defaultdict(int)
bfs(V)