
이 글은 본인이 블록체인 공부 당시 Steemit에 작성 했던 내용을 옮겨온 글입니다.
https://steemit.com/@modolee/floating-point
전반적인 내용을 다 다루려면 분량이 너무 길어 질 것 같아서, 음수 부분은 생략하고 양수에 대한 부분만 작성하겠습니다.
정수를 표현하는 방식
일반적으로 사람이 표현하는 숫자 123을 표현하는 방식에는 여러가지가 있습니다. 우리가 일상적으로 사용하는 숫자 표현방식은 10진수입니다. 123을 여러가지 표현방식으로 나타내면 아래와 같습니다. 자세한 진법 변환 방법은 아래 참고 자료에 첨부하겠습니다.
- 16진수 : 7B
- 10진수 : 123
- 8진수 : 173
- 2진수 : 1111011
컴퓨터가 실수를 표현하는 방식
2진수 표현
컴퓨터는 숫자를 표현할 때 기본적으로 2진수를 사용합니다.
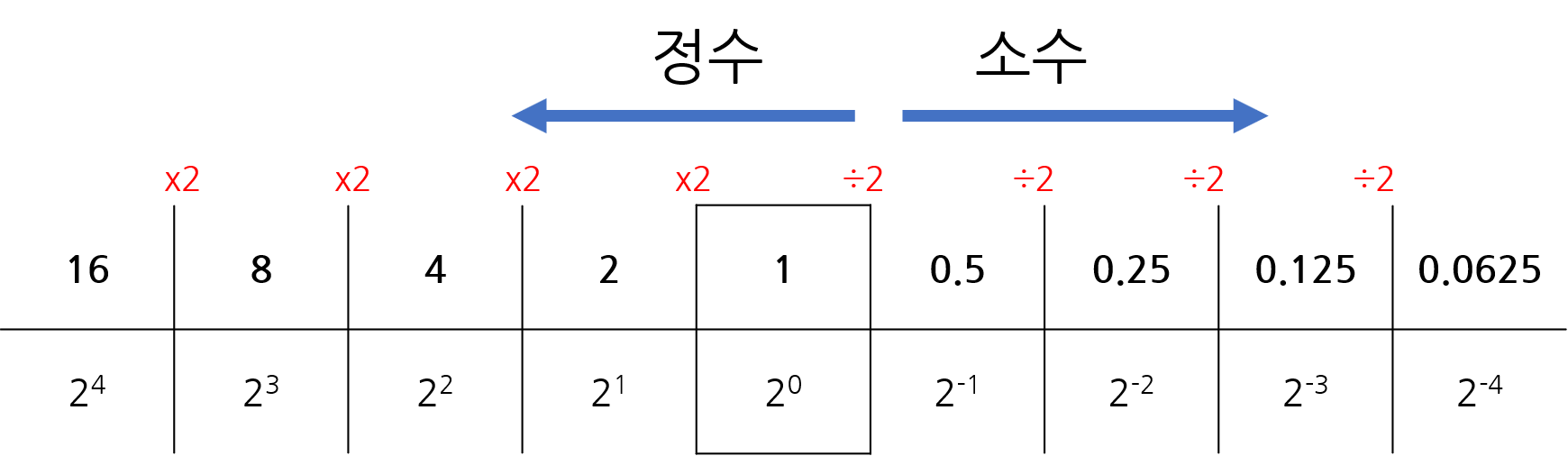
아래 표를 참고해서 숫자를 나타내 보면
-
13 = 8 + 4 + 1 이므로 해당 자리 숫자를 1로 표현하고 나머지는 0으로 표현합니다. 그러면 1101이 됩니다.
-
0.75 = 0.5 + 0.25 이므로 0.11 로 표현할 수 있습니다.
이렇게 쉽게 끝나면 얼마나 좋을까요! ㅠㅠ
263.3 같은 실수를 2진수로 표현해 보면
(상세 방법은 유튜브 영상에 자세히 나와 있습니다.)
- 263 => 100000111
- 0.3 => 0.01001100110011......(0011)의 무한 반복입니다.
이렇게 2진수로 표현하지 못하는 소수가 발생합니다. 어쩔 수 없이 컴퓨터에는 표현할 수 있는 가장 근사치의 값이 저장됩니다.
이 근사 값을 저장하는 방법에는 두 가지가 있습니다.
고정 소수점
- 정수를 표현하는 비트 수와 소수를 표현하는 비트 수를 미리 정해 놓고 해당 비트 만큼만 사용해서 숫자를 표현하는 방식
- 예) 실수 표현에 4byte(32bit)를 사용하고 그 중 부호(아래에서 괄호로 표시) 1bit, 정수 16bit, 소수 15bit를 사용하도록 약속해 놓은 시스템에 있다고 가정합니다. 이렇게 약속 된 시스템에서 263.3을 표현하면 (0)0000000100000111.010011001100110 이렇게 표현됩니다.
- 정수를 표현하는 bit를 늘리면 큰 숫자를 표현할 수 있지만 정밀한 숫자를 표현하긴 힘듭니다. 그래서 소수를 표현하는 bit를 늘릴 경우 정밀한 숫자를 표현할 수 있지만 큰 숫자를 표현하지 못합니다.
이런 문제를 해결하기 위해서 소수점을 고정하지 않고 둥둥 떠 다닐 수 있게 하는 부동 소수점(floating point)을 사용하고 있습니다.
부동 소수점
부동 소수점을 표현하는 방식도 정하는 방식에 따라 다를 수 있지만 일반적으로 사용하고 있는 방식은 IEEE에서 표준으로 제안한 방식입니다.
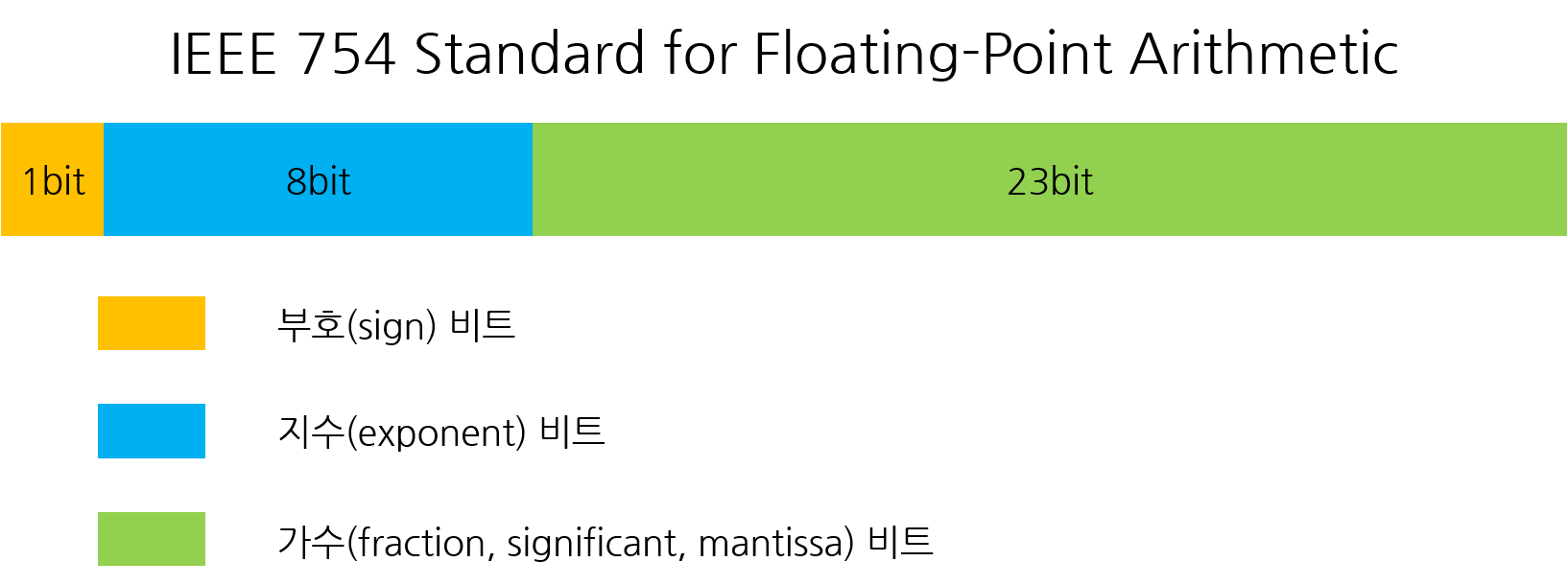
우선 고정 소수점으로 나타낸 263.3을 2진수 부동 소수점 방식으로 변환해 보겠습니다. 100000111.010011001100110... 으로 표현되던 것을 맨 앞에 있는 1 바로 뒤로 소수점을 옮겨서 표현하도록 변환합니다. 그러면 1.00000111010011001100110... * 2^8(2의 8승) 으로 표현 됩니다.
- 2^8의 8을 지수라고 하고 하늘색 부분에 기록합니다. (IEEE 754 표현 방식에서는 127 + 지수를 기록합니다.)
- 소수점 이후 숫자열 전체를 가수라고 하고 연두색 부분에 기록합니다.
이 방식에 따라서 263.3을 기록하면
- 부호 비트(1 bit) : 0 (양수)
- 지수 비트(8 bit) : 10000111 (127 + 8 = 135)
- 가수 비트(23 bit) : 00000111010011001100110
이렇게 표현할 수 있습니다.
하지만! 여기서도 0.010011001100110은 정확히 0.3을 나타낼 수는 없습니다. 10진수로 나타내 보면 0.29998779296875을 나타냅니다.
소수점이 고정 된 것 처럼 보이는데 왜 부동 소수점이라고 불리우나?
263.3 이라는 숫자를 정수 부분과 소수 부분으로 이뤄진 고정 소수점 표현으로 나타내려면 오로지 263.3 한 가지 표현 밖에 없습니다. 그런데 지수, 가수를 이용해서는 2.633 10^2 / 26.33 10^1 / 2633 * 10^-1 이런식으로 소수점을 옮겨가며 표현할 수 있기 때문에 부동 소수점 표현이라고 합니다. 그런데 이것을 컴퓨터에서 표현하기 위해서 약속된 것은 맨 앞에 1자리(2진수로 표현했을 때 1)만 놔두고 나머진 다 소수점 이하로 내려서(정규화해서) 표현하자라고 정하여서 마치 고정된 것 보이는 것 일 뿐입니다.
부동 소수점 오류 예
0.1을 100번 더하면 10이 나와야 되는데...
0.1을 정확히 표현할 수 없기 때문에 발생하는 오류입니다.
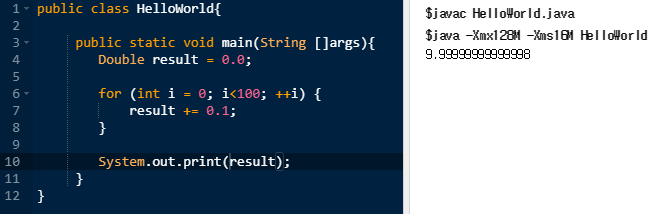
JAVA
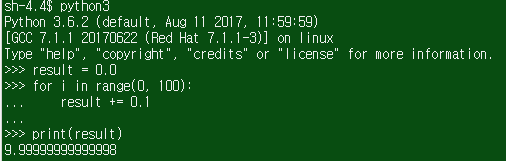
Python
C
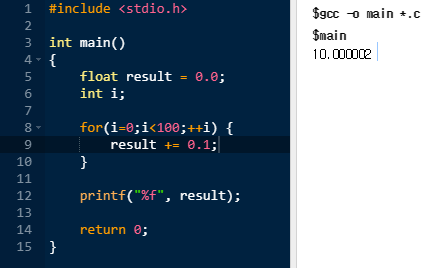
만약 이렇게 오류가 발생할 수 밖에 없는 부동소수점 연산을 블록체인 상에서 사용한다면 어떤 일이 벌어질까요? Token Decimal이 18자리인 EOS의 경우 0.3 EOS를 전송했는데, 갑자기 중간에 0.0000122070312499889 EOS가 훅~ 증발해 버립니다. ㅠㅠ
그래서 이런 일이 일어난 것을 방지하기 위해서 블록체인 구현 시 floating point 연산 지원을 하지 않습니다. 그럼 어떻게 소수점 단위로 코인(토큰)을 주고 받을 수 있을까요?
블록체인 구현 시 부동 소수점 처리
비트코인
- 분할 가능 범위 : 소수점 아래 8자리
- 0.00000001 BTC = 1 Satoshi
- 1 BTC = 100000000 Satoshi
이더리움
- 분할 가능 범위 : 소수점 아래 18자리
- 0.000000000000000001 Ether = 1 Wei
- 1 Ether = 100000000000000000 Wei
참고로 Gas비 계산에 사용되는 Gwei는
- 1 Gwei = 1000000000 Wei
입니다.
사실 실제로 내부적으로 거래가 일어날 때에는 해당 코인의 가장 작은 단위를 이용해서 실수 연산이 아닌 단순 정수 연산을 수행하고 있었습니다. 사용자가 0.00000001 BTC를 전송할 경우 transaction에 0.00000001 BTC가 실려 가는 것이 아니라 그냥 1 Satoshi이 실려 가는 겁니다. 그래서 부동 소수점으로 인한 오류를 신경쓰지 않아도 되는 것이고요.
물론 서버간의 통신에서는 문제가 없겠지만, 다른 3rd party 클라이언트에서 이런 문제를 인식하지 못하고 그냥 구현하게 될 경우 발생하는 문제를 A note on numbers in Ethereum and Javascript에서 다루고 있습니다.
참고
- 진법변환 방법
- How can I represent decimal values in Solidity?
- Bitcoin and floating point accuracy?
- Integer or float used in Bitcoin?
- Floating point inaccuracy examples
- Float not allowed in solidity vs decimal places asked for token contract
- [c언어] 실수 표현 문제 발생 이유 or 오차 발생 이유!
- [머구리씨] C언어-08고정소수점(fixed-point)과 부동소수점(floating-point) 표현방식을 구별하자. 정규화
- Decimal to IEEE 754 Floating Point Representation
- A note on numbers in Ethereum and Javascript
- Inside an Ethereum transaction
