[JS] 우선순위 큐 (Priority Queue)

❗️우선순위 큐 (Priority Queue)

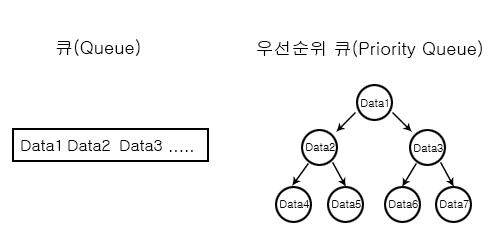
✅ 힙 (Heap)

• 우선순위 큐를 구현하는데 밑받침이 되는 자료구조
• 배열을 이용해 완전 이진 트리 형태로 구현
• 반정렬 상태(느스한 정렬 상태)를 유지

왼쪽 자식의 index = 부모 index *2
오른쪽 자식의 index = (부모 index * 2) +1
부모의 index = Math.floor(자식 index /2)

✅ 최대 힙 (Max Heap) 구현

• 모든 노드가 자식 노드보다 크거나 같은 값을 가지는 힙
• 루트 노드는 최대값을 가짐

추후 수정

✅ 최소 힙 (Min Heap) 구현

• 모든 노드가 자식 노드보다 작거나 같은 값을 가지는 힙
• 루트 노드는 최소값을 가짐

class MinHeap {
  constructor() {
    this.heap = [null];
  }
  swap(a, b) {
    [this.heap[a], this.heap[b]] = [this.heap[b], this.heap[a]];
  }
  size() {
    return this.heap.length - 1;
  }
  isEmpty() {
    return this.size() === 0;
  }

  heappush(value) {
    this.heap.push(value);
    let cur = this.heap.length - 1;
    let par = Math.floor(cur / 2);

    while (cur > 1 && this.heap[cur] < this.heap[par]) {
      this.swap(cur, par);
      cur = par;
      par = Math.floor(cur / 2);
    }
  }

  heappop() {
    if (this.size() === 0) {
      return null; // Return null for an empty heap
    }
    if (this.size() === 1) {
      return this.heap.pop();
    }
    const returnValue = this.heap[1];
    this.heap[1] = this.heap.pop();

    let cur = 1;
    let left = 2;
    let right = 3;

    // 왼쪽 자식이 없는 경우 오른쪽 자식도 없음 > root노트가 최소
    if (!this.heap[left]) return returnValue;
    // 오른쪽 자식이 없는 경우 루트와 왼쪽 자식 값을 비교
    if (!this.heap[right]) {
      if (this.heap[left] < this.heap[cur]) {
        this.swap(left, cur);
      }
      return returnValue;
    }
    // 위 두 조건에 걸리지 않았다면 왼쪽과 오른쪽 자식 모두 보유
    while (
      this.heap[left] < this.heap[cur] ||
      this.heap[right] < this.heap[cur]
    ) {
      // 왼쪽과 오른쪽 자식 중에 더 작은 값과 현재 노드를 교체하면 된다.
      const minIdx = this.heap[left] > this.heap[right] ? right : left;
      this.swap(minIdx, cur);
      cur = minIdx;
      left = cur * 2;
      right = cur * 2 + 1;
    }

    return returnValue;
  }
}