[JS] 트리 (Tree)

❗️ 트리 (Tree)

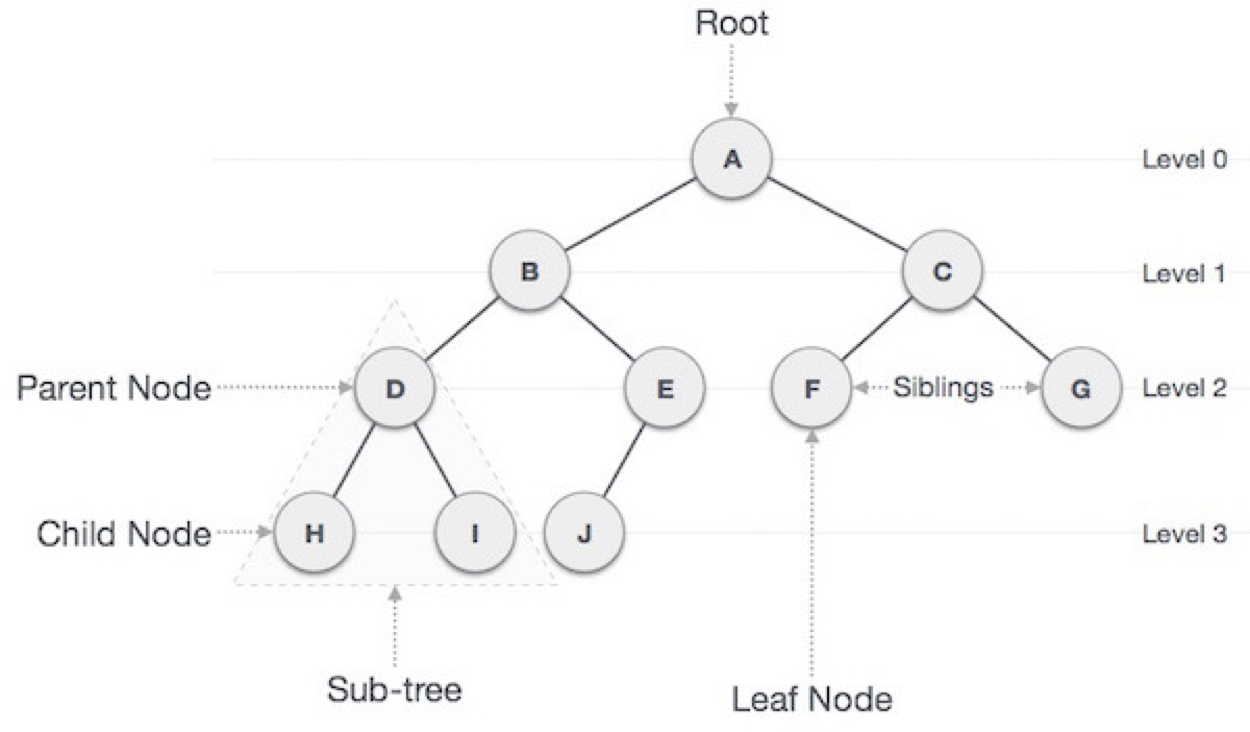
• 단방향 그래프의 구조로 나무와 형태가 닮아 트리 구조라고 부름
• 비선형 구조로 싸이클이 없는 연결 그래프
• 어떤 두 노드를 선택해도 둘 사이에 경로가 항상 하나만 존재

✅ 트리의 기본 구현

class Tree {
  constructor(value) {
    this.value = value;
    this.children = [];
  }

  insertNode(value) {
    const childNode = new Tree(value);
    this.children.push(childNode);
  }

  contains(value) {
    if (this.value === value) {
      return true;
    }

    for (let i = 0; i < this.children.length; i++) {
      const childNode = this.children[i];
      if (childNode.contains(value)) {
        return true;
      }
    }
    return false;
  }
}

✅ 트리의 지름

• 트리에서 임의의 두 점 사이의 거리중 가장 긴 것

1. DFS를 이용해서 최장경로를 저장하는 cost배열 생성
2. 임의의 정점 X가 있을때 X에 대해서 가장 멀리는 있는 정점 Y
3. 정점 Y에 대해서 가장 멀리있는 정점에 대한 거리 = 트리의 지름

❗️이진 트리 (Binary Tree)와 트리 순위 (Tree Traversal)

• 이진 트리 : child의 갯수가 2개로 제한된 형태의 트리

전위 순회 : 루트 왼쪽자식 오른쪽자식
중위 순회 : 왼쪽자식 루트 오른쪽자식
후위 순회 : 왼쪽자식 오른쪽자식 루트

❗️이진 검색 트리 (Binary Search Tree)

• 부모의 크기를 중심으로 노드를 배치
• 왼쪽 자식 < 부모 < 오른쪽 자식

✅ 힙 vs 이진 검색 트리

힙
- 각 노드의 값이 자식보다 크거나 같음 (좌우 자식의 크기는 상관X)
- 최대, 최소값을 빠르게 검색하기 위한 구조
- n개의 노드를 가질 경우 높이가 log(N)이기 때문에 O(log(N))
트리
- 좌우 자식도 크기를 비교
- 특정 트리를 빠르게 탐색하기 위한 구조
- 연결리스트를 이용한 구현은 탐색 : O(N), 삽입과 삭제 : O(1)

❗️ 트리 with dp

• 정점 U를 루트로 하는 서브트리에 속한 정점의 수를 구하는 경우
• DFS를 통해 정점들을 탐색하며 dp에 정점의 수를 업데이트

✅ 백준 15681 - 트리와 쿼리

let tree = Array.from(Array(N + 1), () => []);
let visited = Array(N + 1).fill(false);
let dp = Array(N + 1).fill(0);

arr.forEach((el) => {
  let [from, to] = el;
  tree[from].push(to);
  tree[to].push(from);
});

function DFS(node) {
  if (visited[node]) return dp[node];
  visited[node] = true;
  dp[node] += 1;

  for (let next of tree[node]) {
    if (visited[next]) continue;
    dp[node] += DFS(next);
  }
  return dp[node];
}

DFS(R);