
오늘은 모던 자바스크립트 튜토리얼, 자료구조와 자료형의 숫자형에 대해 공부하겠습니다.
모던 자바스크립트는 숫자를 나타내는 두 가지 자료형을 지원한다.
- 일반적인 숫자는 '배정밀도 부동소수점 숫자(double precision floating point number)'로 알려진 64비트 형식의 IEEE-754에 저장된다.
- 임의의 길이를 가진 정수는 Bigint 숫자로 나타낼 수 있다. 일반적인 숫자는 253이상이거나 -253이하일 수 없다는 제약 때문에 Bigint라는 새로운 자료형이 만들어졌다. Bigint는 아주 특별한 경우에만 사용된다.
숫자를 입력하는 다양한 방법
10억을 입력해야 한다고 상상해보자. 가장 분명한 방법은 아래와 같이 직접 10억(one billion)을 써주는 것이다.
그런데 이렇게 0을 많이 사용해 숫자를 표현하다 보면 잘못 입력하기 쉽기 때문에, 실제로는 이런 방법을 잘 사용하지 않는다. 0을 많이 입력하는 게 귀찮기도 하다. 그래서 대개는 10억(billion)을 나타낼 땐 '1bn'을 사용하고, 73억을 나타낼 땐 '7.3bn'을 사용한다. 큰 숫자를 나타낼 땐 이런 방법이 주로 사용된다.
자바스크립트에서도 숫자 옆에 'e'를 붙이고 0의 개수를 그 옆에 붙여주면 숫자를 줄일 수 있다.

즉, 'e'는 e왼쪽의 수에 e 오른쪽에 있는 수만큼의 10의 거듭제곱을 곱하는 효과가 있다.

아주 작은 숫자인 1마이크로초(백만 분의 1초)를 표현

작은 숫자를 표현할 때도 큰 숫자를 표현할 때처럼 'e'를 사용할 수 있다. 0을 명시적으로 쓰고 싶지 않다면 다음과 같이 숫자를 표현한다.

0.000001 에서 0의 개수를 세면 6이므로 0.000001은 당연히 1e-6이 된다.
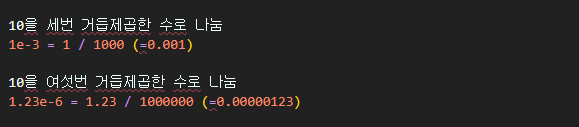
이렇게 'e' 우측에 음수가 있으면, 이 음수의 절댓값 만큼 10을 거듭제곱한 수로 나누는 것을 의미한다.
16진수, 2진수, 8진수
16진수는 색을 나타내거나 문자를 인코딩할 때 등 다양한 곳에서 두루 쓰인다. 다양한 곳에서 쓰이는 만큼 당연히 16진수를 짧게 표현하는 방법도 존재한다. 16진수는 0x를 사용해 표현할 수 있다.
2진수와 8진수는 아주 드물게 쓰이긴 하지만, 접두사 0b와 0o를 사용해 간단히 나타낼 수 있다.

자바스크립트에서 지원하는 진법은 3개이다. 이 외의 진법을 사용하려면 함수 parseInt를 사용해야한다.
toString(base)
num.toString(base) 메서드는 base 진법으로 num을 표현한 후, 이를 문자형으로 변환해 반환한다. base는 2에서 36까지 쓸 수 있는데, 기본값은 10이다.
base별 유스 케이스는 다음과 같다.

※ 점 두 개와 메서드 호출
123456..toString(36)에 있는 점 두 개는 오타가 아니다. 위 예시처럼 숫자를 대상으로 메서드 toString을 직접 호출하고 싶다면 숫자 다음에 점 두 개 ..를 붙어야 한다.123456.toString(36) 처럼 점을 한 개만 사용하면, 첫 번째 점 이후는 소수부로 인식되어 에러가 발생할 수 있다. 점을 하나 더 추가하면 자바스크립트는 소수부가 없다고 판단하고 함수를 호출한다.
(123456).toString(36)도 가능하다.
어림수 구하기
어림수를 구하는 것(rounding)은 숫자를 다룰 때 가장 많이 사용되는 연산 중 하나이다.어림수 관련 내장 함수 몇 가지를 살펴보자.
Math.floor
소수점 첫째 자리에서 내림(버림). 3.1은 3, -1.1은 -2가 된다.
Math.ceil
소수점 첫째 자리에서 올림. 3.1은 4, -1.1은 -1이 된다.
Math.round
소수점 첫째 자리에서 반올림. 3.1은 3, 3.6은 4, -1.1은 -1이 된다.
Math.trunc (Internet Explorer에서는 지원하지 않음)
소수부를 무시. 3.1은 3, -1.1은 -1이 된다.
각 내장 함수의 차이를 표로 나타내면 다음과 같다.

위에서 소개한 내장 함수들만으로도 소수부에 관련된 연산 대부분을 처리할 수 있다. 그런데 소수점 n-th번째 수를 기준으로 어림수를 구해야 하는 상황이라면 어떻게 해야할까
예를 들어 1.2345가 있는데 소수점 두 번째 자릿수까지만 남겨 1.23을 만들고 싶은 경우처럼.
두 가지 방법이 있다.
- 곱하기와 나누기
소수점 두 번째 자리 숫자까지만 남기고 싶은 경우, 숫자에 100 또는 100보다 큰 10의 거듭제곱 수를 곱한 후, 원하는 어림수 내장 함수를 호출하고 처음 곱한 수를 다시 나누면 된다.

- 소수점 n 번째 수까지의 어림수를 구한 후 이를 문자형으로 반환해주는 메서드인 toFixed(n)를 사용한다.

toFixed는 Math.round와 유사하게 가장 가까운 값으로 올림 혹은 버림을 해준다.

toFixed를 사용할 때 주의할 점은 이 메서드의 반환 값이 문자열이라는 것이다. 소수부의 길이가 인수보다 작으면 끝에 0이 추가된다.

참고로, +num.toFixed(5) 처럼 단항 덧셈 연산자를 앞에 붙이거나 Number()를 호출하면 문자형의 숫자를 숫자형으로 변환할 수 있다.
부정확한 계산
숫자는 내부적으로 64비트 형식 IEEE-754으로 표현되기 때문에 숫자를 저장하려면 정확히 64비트가 필요하다. 64비트 중 52비트는 숫자를 저장하는 데 사용되고, 11비트는 소수점 위치를 (정수는 0), 1비트는 부호를 저장하는 데 사용된다.그런데 숫자가 너무 커지면 64비트 공간이 넘쳐서 Infinity로 처리된다.

원인을 이해하려면 집중이 필요하긴 하지만, 꽤 자주 발생하는 현상인 정밀도 손실(loss of precision)도 있다.

0.1과 0.2의 합이 0.3과 일치하는지 확인했는데 false가 출력되었다.
왜 0.3이 아닐까

부정확한 비교 연산이 만들어내는 결과가 여기서 그치지 않는다. 인터넷 쇼핑몰 사이트를 운영하고 있다고 가정해보자. 사용자가 $0.10와 $0.20 짜리 물품을 장바구니에 넣었다고 상상해보자. 주문 총액이 $0.30000000000000004 인 것을 보고 놀라지 않을 사용자는 없을 것이다.
왜 이런일이 발생하는 걸까
숫자는 0과 1로 이루어진 이진수로 변환되어 연속된 메모리 공간에 저장된다. 그런데 10진법을 사용하면 쉽게 표현할 수 있는 0.1 0.2 같은 분수는 이진법으로 표현하면 무한 소수가 된다.
0.1 은 1을 10으로 나눈 수인 1/10 이다. 10진법을 사용하면 이러한 숫자를 쉽게 표현할 수 있다. 1/10과 1/3을 비교해보자. 1/3은 무한 소수 0.33333(3)이 된다.
이렇게 10의 거듭제곱으로 나눈 값은 10진법에서 잘 동작하지만 3으로 나누게 되면 10진법에서 제대로 동작하지 않는다. 같은 이유로 2진법 체계에서 2의 거듭제곱으로 나눈 값은 잘 동작하지만 1/10 같이 2의 거듭제곱이 아닌 값으로 나누게 되면 무한 소수가 되어버린다.
10진법에서 1/3을 정확히 나타낼 수 없듯이, 2진법을 사용해 0.1 또는 0.2를 정확하게 저장하는 방법은 없다.
IEEE-754에선 가능한 가장 가까운 숫자로 반올림하는 방법을 사용해 이런 문제를 해결한다. 그런데 반올림 규칙을 적용하면 발생하는 '작은 정밀도 손실'을 우리가 볼 수는 없지만 실제로 손실은 발생한다.
아래와 같이 코드를 작성하면 정밀도 손실을 눈으로 확인할 수 있다.

그리고 두 숫자를 합하면 '정밀도 손실'도 더해진다.
0.1 + 0.2 가 정확히 0.3 이 아닌 이유가 여기에 있다.
TMI - 자바스크립트뿐만이 아니다.
다른 언어에서도 같은 이슈가 있다.자바스크립트와 동일한 숫자 형식을 사용하기 때문에 PHP, Java, C, Perl, Ruby에서도 똑같은 결과를 얻는다.
가장 신뢰할만한 문제 해결 방법은 toFixed(n)메서드를 사용해 어림수를 만드는 것이다.

이때 toFixed는 항상 문자열을 반환한다는 점에 유의해야 한다. 문자열을 반환하기 때문에 소수점 다음에 오는 숫자가 항상 2개가 될 수 있다. 인터넷 쇼핑몰을 구축 중이고 $0.30를 보여줘야할 때 유용하다. 문자형으로 바뀐 숫자를 다시 숫자형으로 강제 변환하려면 단항 덧셈 연산자를 사용하면 된다.

숫자에 암시로 100(또는 더 큰 숫자)를 곱하여 정수로 바꾸고, 원하는 연산을 한 후 다시 100으로 나누는 것도 하나의 방법이 될 수 있다. 정수를 대상으로 하는 수학 연산은 소수를 대상으로 하는 연산보다 에러가 적기 때문이다. 그런데 어쨋든 마지막에 나눗셈이 들어가기 때문에 소수가 다시 등장할 수 있다는 단점이 있다.

이렇게 10의 거듭제곱을 곱하고 다시 동일한 숫자로 나누는 전력은 오류를 줄여주긴 하지만 완전히 없애지는 못한다.
구현을 하다 보면 무한 소수가 나오는 경우를 완전히 차단해야 하는 경우가 생기곤 한다. 달러가 아닌 센트 단위로 물품 가격을 저장하는 쇼핑몰을 담당하고 있는데, 행사 때문에 가격을 30% 할인해야 하는 경우가 그렇다. 무한소수를 방지하는 완벽한 방법은 사실 없다. 필요할 때마다 '꼬리'를 잘라 어림수를 만드는 방법뿐이다.
isNaN과 isFinite
두 특수 숫자는 숫자형에 속하지만 '정상적인' 숫자는 아니기 때문에, 정상적인 숫자와 구분하기 위한 특별한 함수가 존재한다.

그런데 굳이 이 함수가 필요할까? === NaN 비교를 하면 되지 않을까? 라는 생각이 들 수 있다.
질문에 대한 대답은 '필요하다'이다. NaN은 NaN 자기 자신을 포함하여 그 어떤 값과도 같지 않다는 점에서 독특하다.


isFinite는 문자열이 일반 숫자인지 검증하는 데 사용되곤 한다.

빈 문자열이나 공백만 있는 문자열은 isFinite를 포함한 모든 숫자 관련 내장 함수에서 0으로 취급된다는 점에 유의하자
parseInt와 parseFloat
단항 덧셈 연산자 + 또는 Number()를 사용하여 숫자형으로 변형할 때 적용되는 규칙은 꽤 엄격하다. 피연산자가 숫자가 아니면 형 변환이 실패한다.
엄격한 규칙이 적용되지 않는 유일한 예외는 문자열의 처음 또는 끝에 공백이 있어서 공백을 무시할 때이다.
그런데 실무에선 CSS 등에서 '100px', '12pt'와 같이 숫자와 단위를 함께 쓰는 경우가 흔하다.
대다수 국가에서 '19€' 처럼 금액 뒤에 통화 기호를 붙여 표시하기도한다. 숫자만 추출하는 방법이 필요하다.
내장 함수 parseInt와 parseFloat는 이런 경우를 위해 만들어졌다.
두 함수는 불가능할 때까지 문자열에서 숫자를 '읽는다.' 숫자를 읽는 도중 오류가 발생하면 이미 수집된 숫자를 반환한다. parseInt는 정수, parseFloat는 부동 소수점 숫자를 반환한다.

parseInt와 parseFloat가 NaN을 반환할 때도 있다. 읽을 수 있는 숫자가 없을 때 그럴것이다.

기타 수학 함수
자바스크립트에서 제공하는 내장 객체 Math엔 다양한 수학 관련 함수와 상수들이 들어있다.몇가지 예시를 살펴보자.
Math.random()
0과 1 사이의 난수를 반환한다.

Math.pow(n, power)
n을 power번 거듭제곱한 값을 반환한다.

