HPD 신용구간은 가장 그럴듯한 𝜃들을 모아 놓은 구간이다.
1. 신뢰구간(Confidence Interval)과 신용구간(Credible Interval)
* 먼저 빈도주의적(Frequentist)관점에서의 신뢰구간과 베이지안(Bayesian) 관점에서의 신용구간을 비교해보자.
1.1 신뢰구간(Confidence Interval)
* 모평균 𝜇에 대한 구간추정을 한다고 가정하자.
* 유의수준 𝛼는 0.05, 추정량 𝜃 hat의 분포는 Normal이라고 가정하자.
동일한 크기의 Sample을 100번 독립적으로 추출하고, 위 신뢰구간 형태식에 의거하여 신뢰구간 100개를 구한다면 근사적으로 100개 중 95는 모평균을 포함할 것이다.
일반적으로 말하는 모평균 𝜇에 대한 95% 신뢰구간이 의미하는 바는 위와 같다. 그림으로 표현하면 아래와 같이 표현할 수 있다.
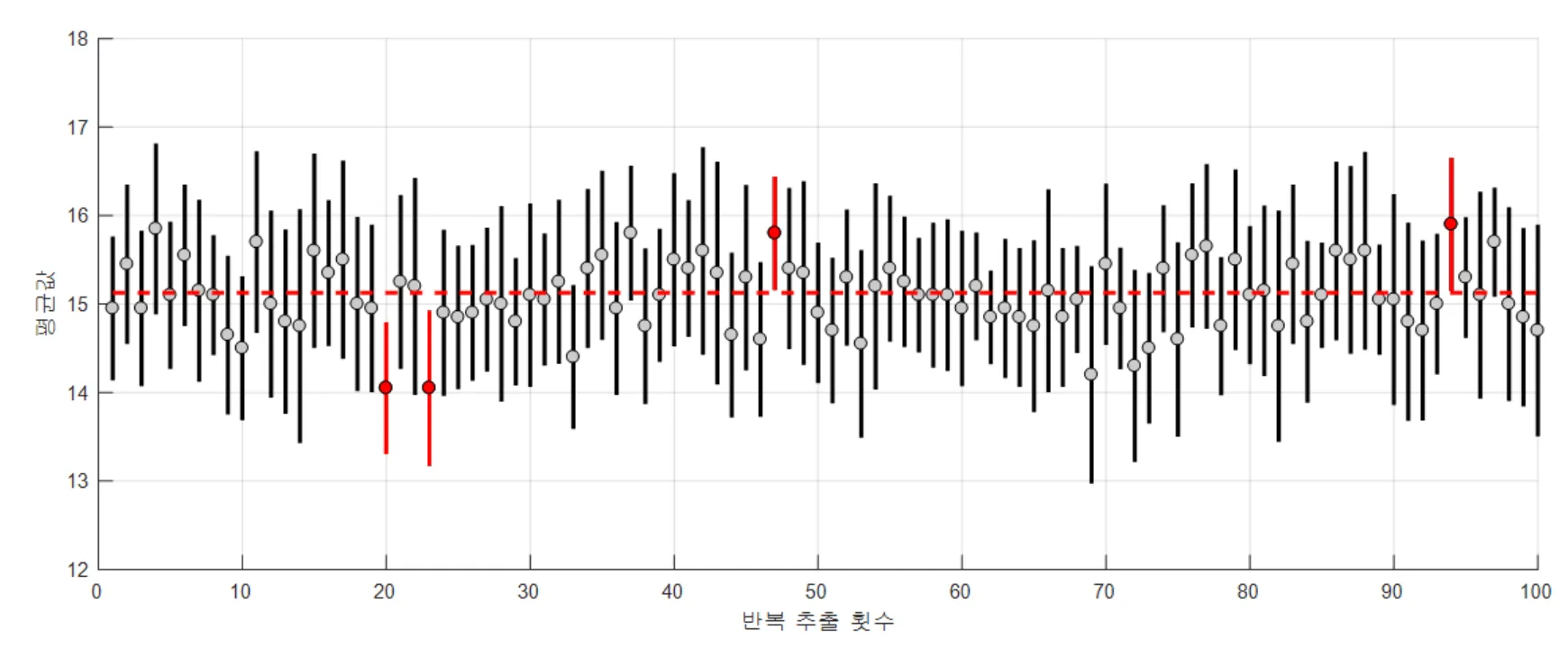
[각 선은, 독립적인 100개의 Sample 각각에 신뢰구간 형태식을 적용해 구해진 신뢰구간이며, 붉은색은 모평균을 포함하지 않는 신뢰구간을 의미한다.]
1.2 신용구간(Credible Interval)
앞서 살펴본 신뢰구간의 의미를 생각해보면 다소 이상한 점을 느낄 수 있는데, 사실상 관찰되지 못한 Sample들을 이용하여 결론을 내린다는 점이다.
우리는 실제로 Sample을 하나만 뽑았지만, 표본추출은 무수히 많은 조합을 추출할 수 있기에 100번 가량 반복 Sampling하면 대략 95번의 신뢰구간은 모평균을 포함하리라는 것이다.
한편, 아래의 해석은 신뢰구간을 잘못 해석한 경우이다.
모평균은 95% 확률로 해당 구간에 포함된다.
하지만 이것이 구간추정(Interval Estimation)을 이해하는, 보다 직관적인 해석이라 생각된다. 이 같은 해석을 가능하게끔 하는 구간추정 방법이 바로 베이지안 관점의 신용구간이다.
2. HPD(Highest Posterior Density) 신용구간
2.1 신용구간의 해석
* 베이지안 추론(Bayesian Inference)바탕의 점추정, 구간추정, 가설검정은 모두 Posterior distribution 바탕으로 이루어진다. 따라서 Posterior distribution을 우선적으로 계산해야한다.
베이지안 관점에서 Parameter 𝜃는 Random Variable이다. 그리고 Posterior Distribution은 관측치 𝒚를 이용하여 prior를 업데이트하여 구해진 Parameter의 분포이다.
즉 Posterior distribution은 X축을 𝜃|𝒚 로, Y축을 𝜃|𝒚의 probability로 하는 분포를 이야기하며, 구간추정의 개념을 이 분포에 대해 적용해보자는 이야기이다. 이 분포는 모수 𝜃의 분포를 나타내기에 해당 분포에 ‘구간’의 개념을 씌워본다면 앞서 살펴본 아래와 같은 해석이 자연스러워진다.
모평균(모수)은 95% 확률로 해당 구간에 포함된다.
2.1 HPD(Highest Posterior Density)
그렇다면 어떻게 Posterior Distribution에서 구간을 정할 수 있을까?
→ Posterior의 Density가 높은 𝜃부터 차곡차곡 쌓아서 구간을 정하자.
(Probability를 가장 높여주는 𝜃부터 구간에 포함시키자)
(Posterior Distribution을 산과 같이 생각하고 눈처럼 덮어내려오면서 1-𝛼 수준을 만족할 떄 멈추자)
아래의 Posterior distribution을 생각해보자. 모수 𝜃에 대한 94% 신용구간을 구한다고 했을 때에 우리는 산 정상(Posterior density가 가장 높은 부분)부터 수평선을 아래로 그어가며 94%가 되었을 때에 멈추어 ‘구간’을 정할 수 있을 것이다.
* 𝛼는 0.04라고 가정하자.
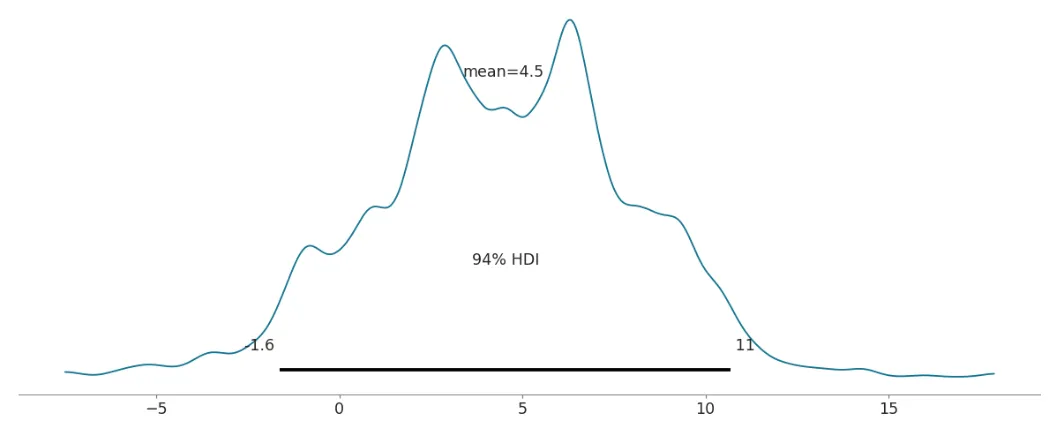
𝜃에 대한 100(1-0.04) HPD 신용구간은 아래와 같다.

이를 수식으로 표현하면 다음과 같다.
* C는 신용구간을 의미하고, 𝛼는 유의수준을 의미한다.
* Sample 𝒚와 prior를 이용해 얻어진 Posterior Distribution 기반의 구간추정 해석은,
모수가 1-𝛼 확률로 해당 구간에 포함될 것이라고 이야기하는 것과 같다.
참고자료
공돌이의 수학정리노트 - 신뢰구간의 의미[Link]
Arviz, Exploratory analysis of Bayesian models 웹사이트 [Link]
