Elliptic Curve Cryptosystem ( 타원 곡선 암호 시스템 )
유한체상의 타원곡선 이론에 기반한 공개키 암호
타원 곡선 암호 시스템의 특징
-
RSA의 키는 보통 1024bits 이상이지만 ECC는 256bit 이상의 크기를 갖으며 상대적으로 짧은 키의 길이로 같은 보안 수준을 제공할 수 있다.
-
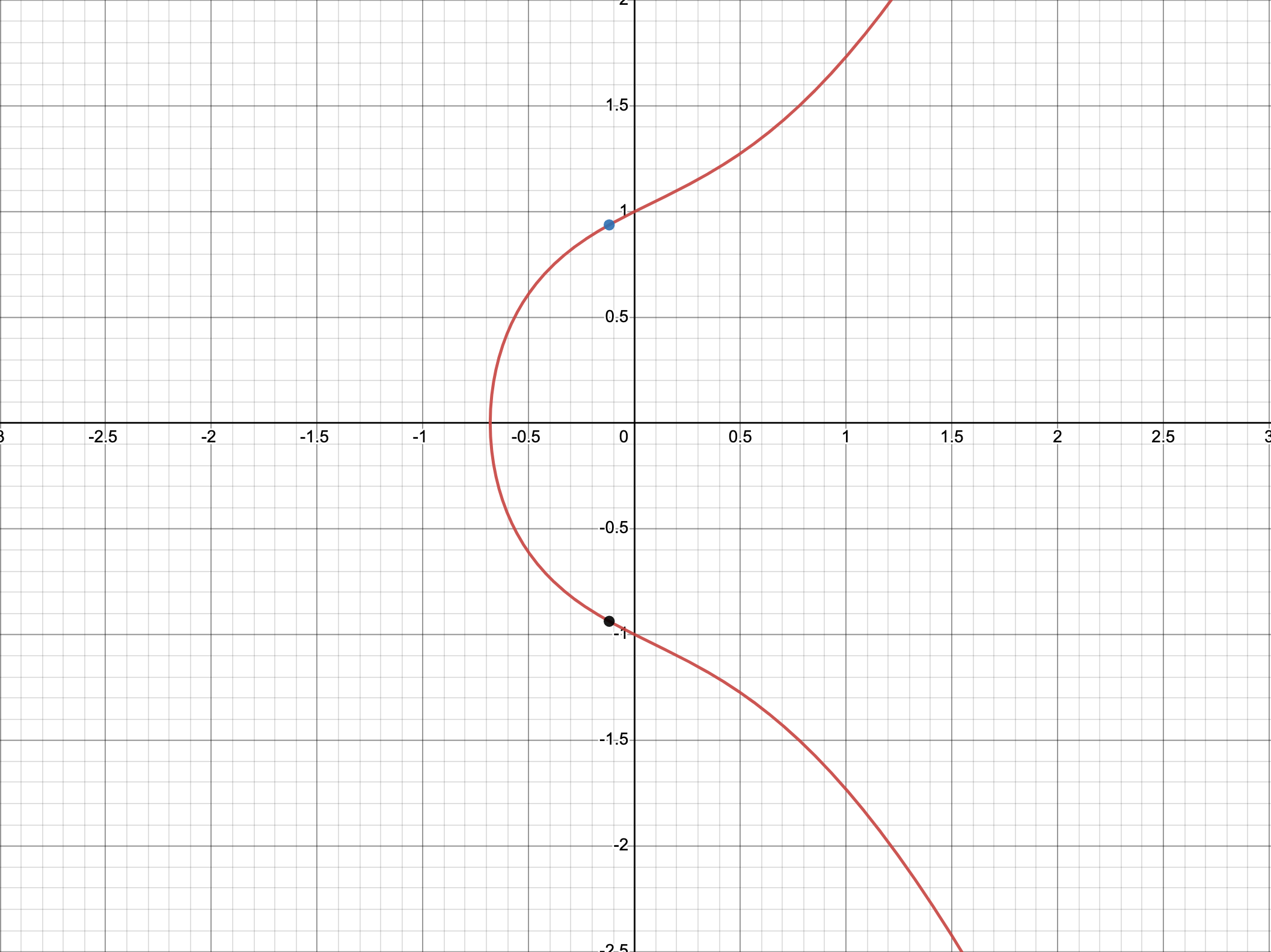
실수 상의 타원곡선
- 모든 근이 실근일 경우, 좌표의 수평선과 곡선이 3점에서 교차한다
그래프 ⬇
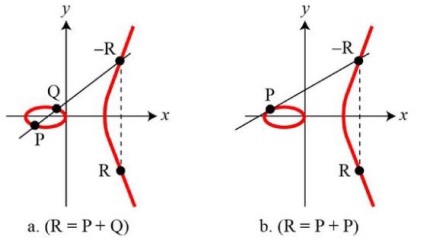
타원 곡선 상의 덧셈 연산
타원곡선 상에서 두 점(,)을 정한 후 두 점을 지나가는 직선이 타원 곡선과 만나는 3번째 교점을 축 기준으로 대칭되는 점을 로 정의하여 계산하는 것을 기초한다
= (, ) , Q = (, )
=
🖋 = (, ) 계산 방법
.
(기울기) =
.
(기울기) =
GF()상의 타원 곡선
GF는 Galois Field, 유한체를 의미하며 는 Prime Number 즉 소수를 의미한다
Modulo 를 이용한 타원곡선 특징
-
의 값은 0~ -1 사이에 존재한다.
-
덧셈연산은 덧셈 결과를 mod 연산 해준다.
-
역원은 기준 이며 여기서 는 의 덧셈에 대한 역원이다
↪가 13일때 의 역원은 이며 즉 이다