[JAVA][프로그래머스] 연속 펄스 부분 수열의 합

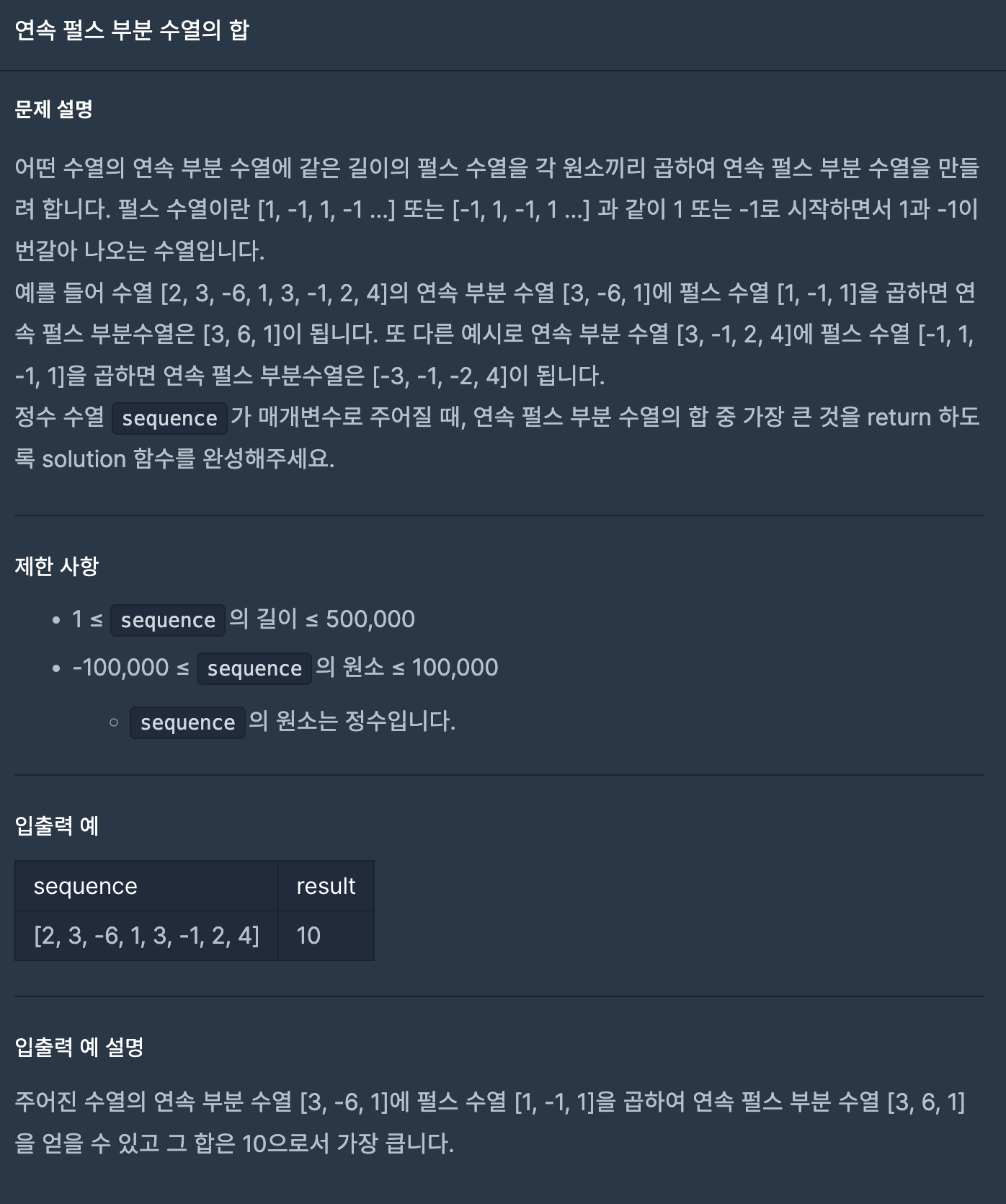
1. 문제 링크

2. 해결 방법 생각해보자 ...

처음에 sequence의 길이가 길어 동적계획법을 생각했다.
하지만 점화식이 곧바로 그려지지 않았고 한 방법을 떠오르듯 다른 분들의 코드를 참고했다.
그럼 문제를 해결해보자.

---

펄스수열이 나올 수 있는 경우의 수는 어떻게 될까?

모든 값에 1 을 곱해보고 -1 도 곱해보고 또 곱해서 나온 값들의 연속된 부분의 합을 구해야 한다.

1. 1부터 시작해서 1,-1,1,-1 ... 해서 부분의 합
2. -1부터 시작해서 -1,1,-1,1 ... 해서 부분의 합

여기서 연속된 부분의 합 하면 바로..는 아니고 3초 정도 뒤에 생각나는 알고리즘 기법이 있다.

누적합!

이게 생각났다면 문제는 다 풀었다.
1. 1, -1, 1, -1 ... 을 곱한 누적합 배열을 생성한다.

• plusSum[i+1] += plusSum[i] + sequence[i]*flag;

2. -1, 1, -1, 1 ... 을 곱한 누적합 배열을 생성한다.

• plusSum과 정확히 부호가 반대임을 알 수 있다! -> flag*= -1 ; 반대로 만들어준 후
• mSum[i+1] += mSum[i]+ sequence[i]*flag;

그럼 우리는 해당 두 배열을 통해, 1,-1을 곱하고 더했을 모든 경우의 수의 값을 구할 수 있다 !!
어떻게!?
plusSum에서
plusSum[1]-plusSum[0],
plusSum[2]-plusSum[0],
plusSum[3]-plusSum[0],
plusSum[2]-plusSum[1] 등등을 다 해보면 된다!

하나하나 다 구현해요...?

아니요! 우리에겐 투포인터가 있다.

left = 0 ; right = 1 ;
로 설정해두고,
1. plusSum[right]-plusSum[left] > 0 인 경우?

• right ++ 하며 구할 수 있는 최댓값을 구한다.

2. < 0 인 경우?

• 그 아래는 볼 필요가 없는 것 이므로, left=right, right ++;
  로 새로운 탐색을 시작한다!

그럼 끝이다!
(이어서 DP 풀이도 있다!)

3. 코드

import java.util.*;
import java.io.*;

class Solution {
    static long answer ;
    public long solution(int[] sequence) {
        answer = 0;
        int len = sequence.length;
        long[] plusSum = new long[len+1];
        long[] mSum = new long[len+1];
        int flag = 1 ;
        for(int i=0;i<len;i++){
            plusSum[i+1] += plusSum[i] + sequence[i]*flag; // 1,-1,1,-1 ...
            
            flag*= -1 ;
            mSum[i+1] += mSum[i]+ sequence[i]*flag; // -1,1,-1,1...
        }
        
        twoPointer(plusSum,len); // 1,-1,1.. 에서 얻을 수 있는 최댓값
        twoPointer(mSum,len); // -1,1,-1.. 에서 얻을 수 있는 최댓값

        return answer;
    }
    
    public static void twoPointer(long[] arr, int len){
        int left = 0 ;
        int right = 1;
        while(right<=len){ // 최대 길이는 넘기면 앙대요.
            long sum = arr[right]-arr[left]; // 부분 누적합 공식
            if(sum > answer){
                answer = sum;
            }
            
            if(sum>0){
                right ++;
            }else{
                left=right++;
            }
        }
    }
}

---

하지만 DP로도 풀이가 가능하지 않을까? 했는데
프로그래머스 질문 게시판에 힌트를 주신 분이 있어 코드로 풀어보았고 함께 첨부한다~! 👍감사합니당

import java.util.*;
import java.io.*;

class Solution {
    static long answer ;
    public long solution(int[] sequence) {
        answer = 0;
        int len = sequence.length;
        long[] plusDP = new long[len+1];
        long[] mDP = new long[len+1];
        int flag = 1 ;

        for(int i=1;i<len+1;i++){
            plusDP[i] = Math.max(plusDP[i-1]+sequence[i-1]*flag, sequence[i-1]*flag);
            flag *= -1 ;
            mDP[i] = Math.max(mDP[i-1]+sequence[i-1]*flag, sequence[i-1]*flag);
            answer = Math.max(answer, Math.max(plusDP[i],mDP[i]));
        }
        return answer;
    }

}