1. 문제 링크 및 문제
https://www.acmicpc.net/problem/1238
문제요약
N명의 학생이 X번 마을에 모여 파티 진행
마을 사이 M개의 단방향 도로, i번째 길 T 의 시간
N명의 학생들 중 오고 가는데 가장 오래 걸리는 학생 ( 최단 시간 )
2. 해결 방법 생각해보자 ...
해결방법 ( 시간제한 1초, N(1 ≤ N ≤ 1,000), M(1 ≤ M ≤ 10,000)
1. 각자의 마을에서 X 마을까지 가는 거리 계산
2. X 마을에서 각자의 마을까지 오는 계산
각 마을의 1+2 의 최댓값!간단하지용?
어제 다익스트라 포스팅을 정리한 직후라 다익스트라는 해당 정점에서 다른 정점들로 가는 최단거리이므로,
2번은 가볍게 다익스트라로 접근하면 되겠구나 생각했다.
1번은 각 정점에서 정해진 정점까지 가는 최단 거리를 구해야했다.
최단 경로 알고리즘 중 다른 알고리즘을 적용해야하나? 도 고민했지만
시간복잡도 상으로 알맞지 않아서 다익스트라로 풀었다.
내가 해결한 방법은 아래에 적혀있고 (맞긴 맞았지만 더 오래 소요된다),
더 깔끔한 풀이는 간선을 뒤집으면 된다!
간선을 뒤집는다 는 게 무슨말이냐?
백준예시 1을 통해 살펴보겠습니다.
그래프를 한 번 그려보시면 바로 이해하실 수 있을 것입니다.
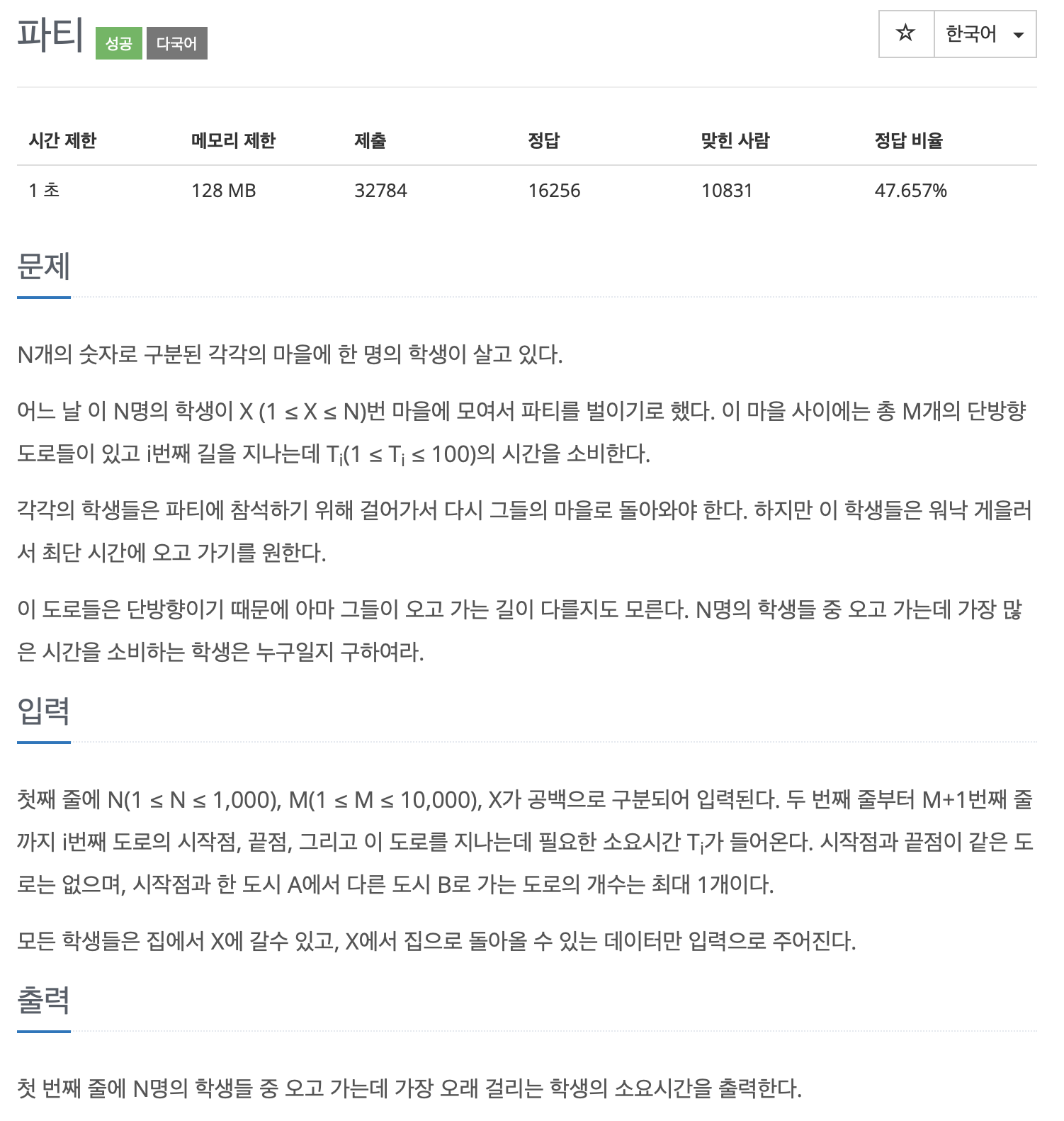
아래는 문제에서 주어진 그래프를 그대로 그린 것입니다.
2번 정점에서 시작하여, 1번 3번 4번 정점을 방문하는 거리
즉, 파티를 갔다 집으로 돌아오는 과정이지요.
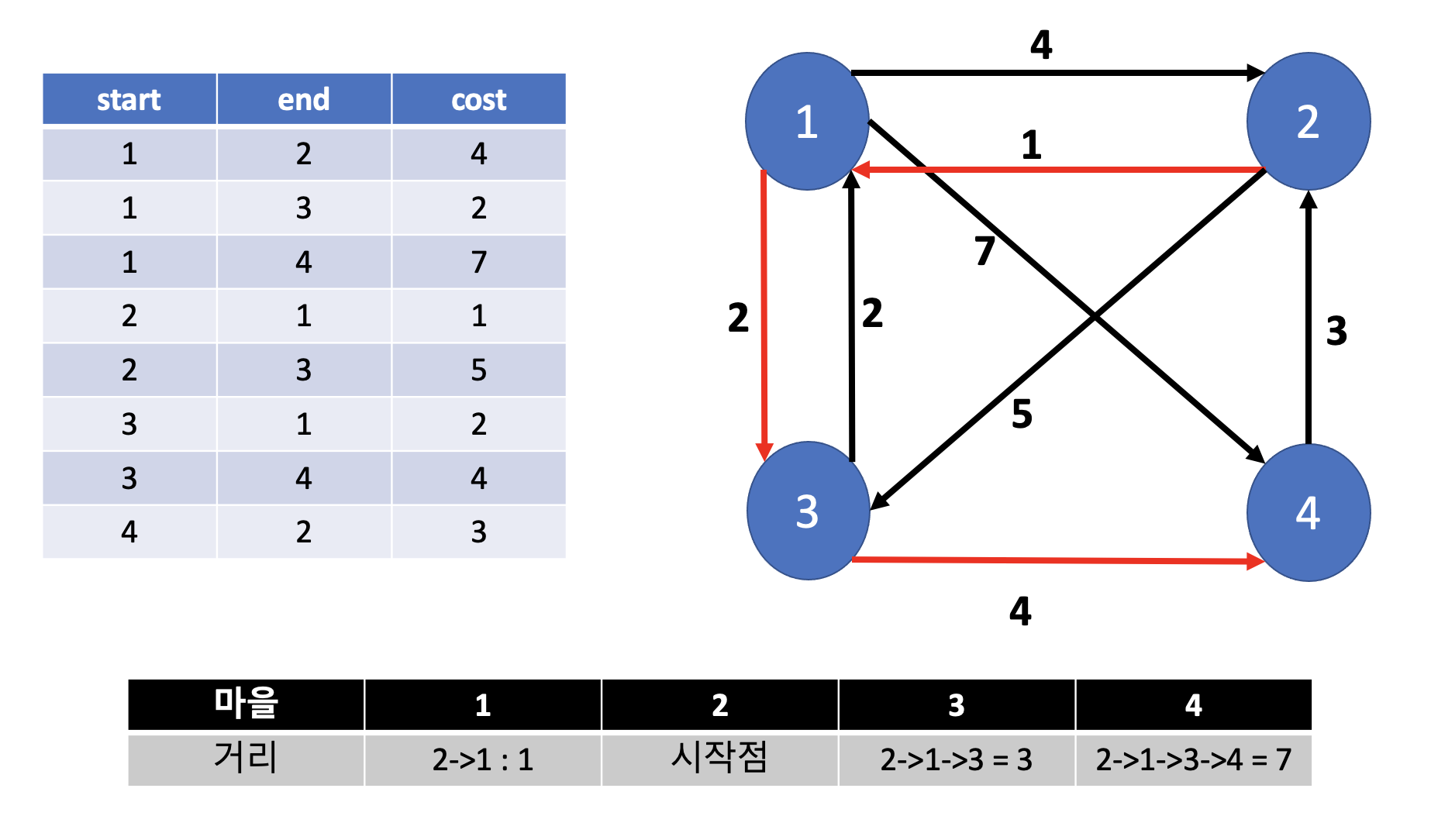
그럼 파티를 가는 과정을 구해봅시다.
위 그래프에서 보면
1번에서 부터 2번까지의 거리,
3번에서 부터 2번까지의 거리,
4번에서 부터 2번까지의 거리를 구해야 하는 것이겠지요?
그럼 한 번 구해보겠습니다.
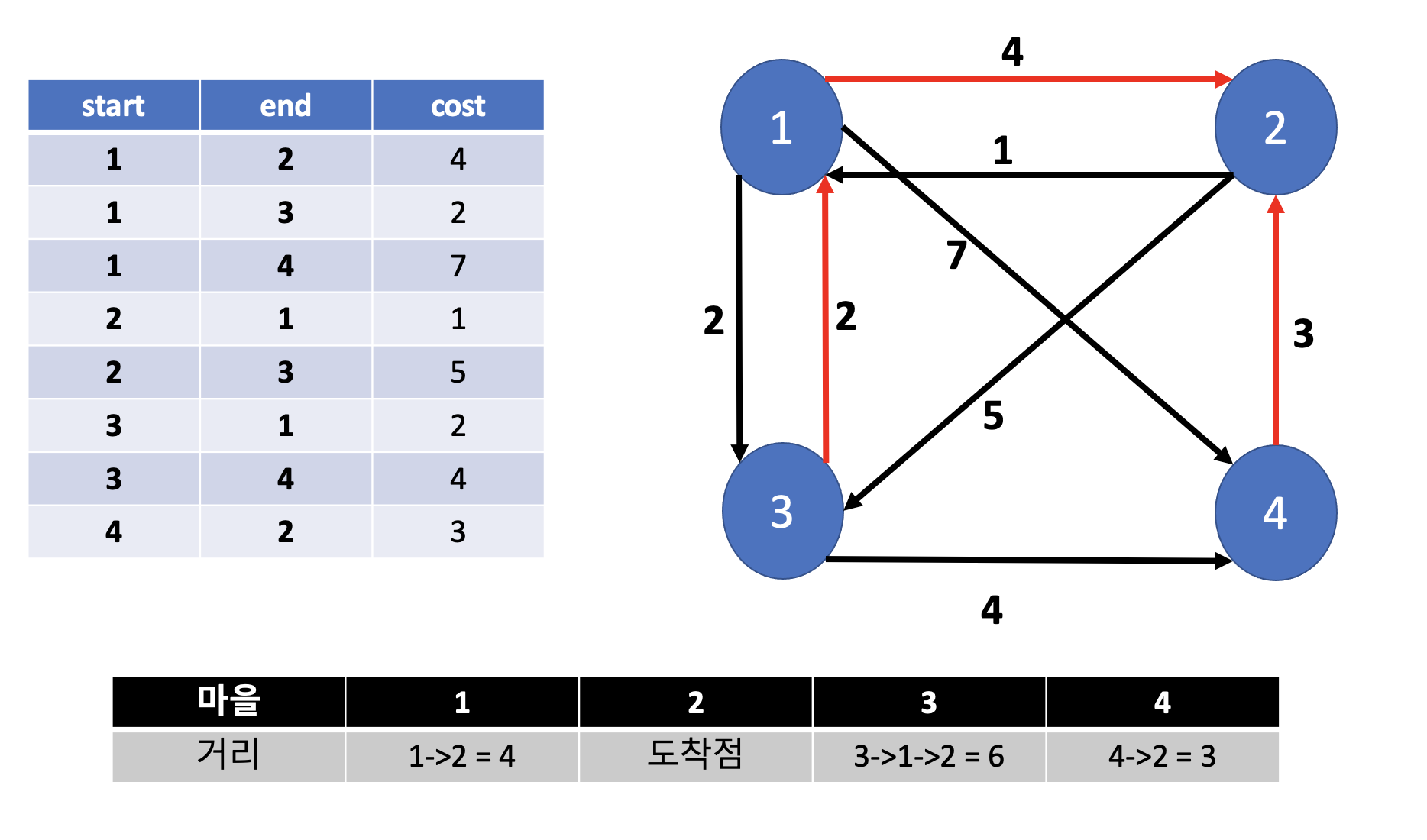
이는 도착정점은 같지만, 시작 정점이 다릅니다.
그럼 다익스트라 적용에 살짝 힘든데
이를 반대로 생각하면 원래 입력받았던 배열을 거꾸로 간다면? 해결할 수 있습니다.
1번에서 부터 2번까지의 거리,
3번에서 부터 2번까지의 거리,
4번에서 부터 2번까지의 거리를 하나하나 구하는 방법대신
start,end 를 뒤집어서 받아보겠습니다.
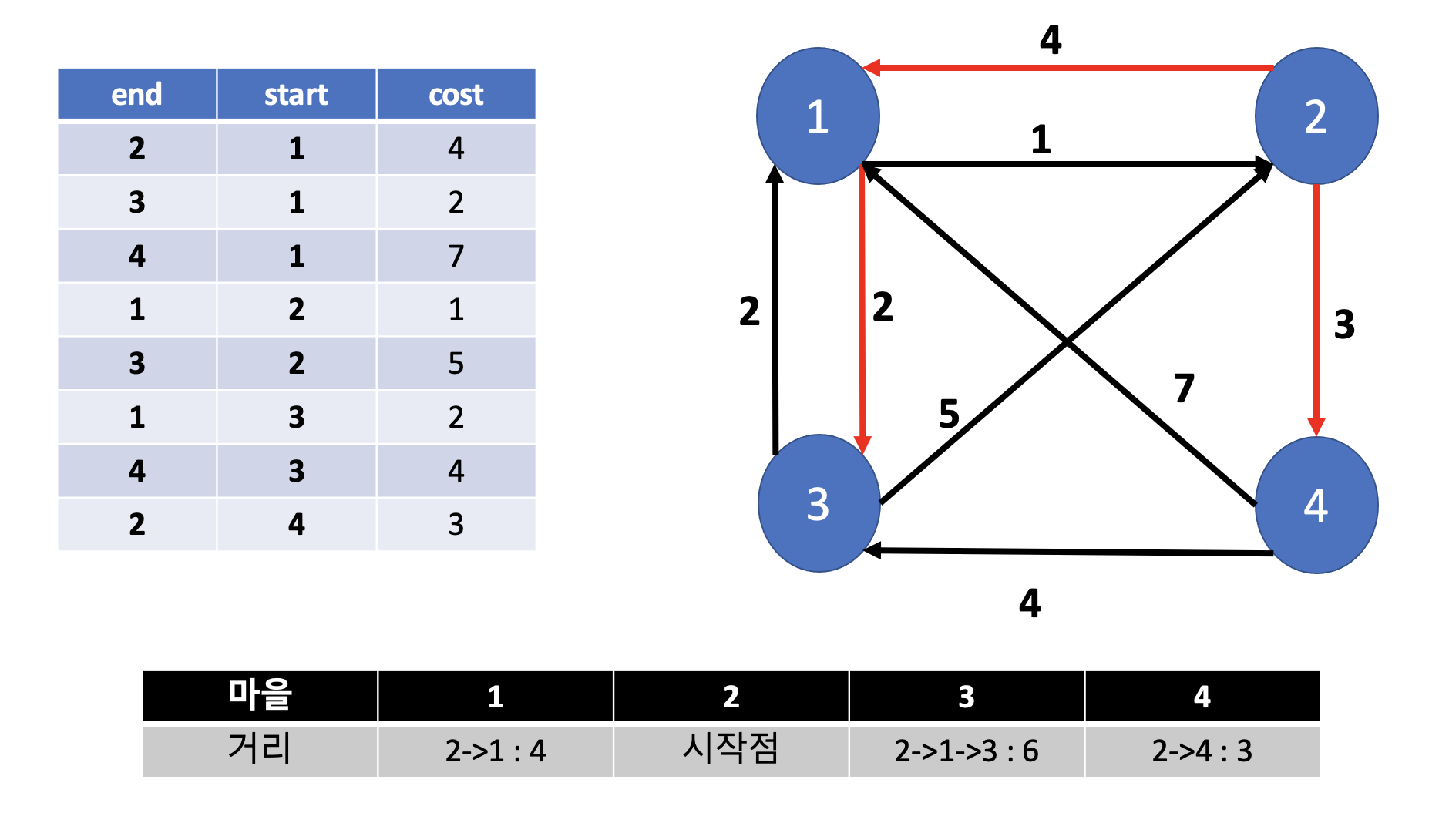
짠💡 그럼, 저희는 원래의 다익스트라처럼
2번정점에서 출발하여 각 정점까지의 거리를 구할 수 있습니다.
즉, 배열을 입력받을 때 arr[start][end] 랑 reverseArr[end][start] 도 입력받아서,
다익스트라를 arr, reverArr 로 최단거리를 구하면 됩니다.
시간이 더 오래 소요되었지만, 처음 풀었던 방법
- 가는 거 계산
- X마을까지 다익스트라 실행
- O(N-1)*(MlogN)
- 오는 거 계산
- X마을부터 다익스트라 실행
- O(MlogN)
3. 코드
import java.util.*;
import java.io.*;
class Node{
int idx,cost;
Node(int idx, int cost){
this.idx = idx;
this.cost = cost;
}
}
public class Main{
static int N,M,X ; // N: 학생수, M : 도로수, X: X번 마을에서 모임
static ArrayList<Node>[] map, ReMap; // 원래 맵, 반대맵
public static int stoi(String str){
return Integer.parseInt(str);
}
public static void main(String args[]) throws Exception{
// 값 입력받기 -->
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
N = stoi(st.nextToken());
M = stoi(st.nextToken());
X = stoi(st.nextToken())-1;
map = new ArrayList[N];
ReMap = new ArrayList[N];
for(int i=0;i<N;i++) {
map[i] = new ArrayList();
ReMap[i] = new ArrayList();
}
for(int i=0;i<M;i++){
st = new StringTokenizer(br.readLine());
int x = stoi(st.nextToken())-1;
int y = stoi(st.nextToken())-1;
int cost = stoi(st.nextToken());
map[x].add(new Node(y,cost));
ReMap[y].add(new Node(x,cost));
}
//<--
int[] ComeDist = dijkstra(map); // 오는 거
int[] GoDist = dijkstra(ReMap); // 가는 거
int ans = 0 ;
for(int i=0;i<N;i++){ // 최댓값 계산
if(i==X) continue;
ans = Math.max(ans, ComeDist[i] + GoDist[i]);
}
System.out.println(ans);
}
// 다익스트라 알고리즘
public static int[] dijkstra(ArrayList<Node>[] arr){
PriorityQueue<Node> pq = new PriorityQueue<>(((o1, o2) -> Integer.compare(o1.cost, o2.cost)));
pq.offer(new Node(X, 0)); // 시작 정점 삽입
int[] dist = new int[N+1]; // 거리 배열 초기화
Arrays.fill(dist,Integer.MAX_VALUE);
dist[X] = 0;
while(!pq.isEmpty()){ // 최단경로 계산
Node now = pq.poll();
int cur = now.idx;
for(Node nxt : arr[cur]){
if(dist[nxt.idx] < now.cost) continue;
if(dist[nxt.idx] > now.cost + nxt.cost){
dist[nxt.idx] = now.cost + nxt.cost;
pq.offer(new Node(nxt.idx, dist[nxt.idx]));
}
}
}
return dist;
}
}