[Data structure] B tree & B+ tree

Mongle·2021년 1월 13일

OS프로젝트

목록 보기

2/8

[Data_structure] B tree & B+tree

팀원들의 피땀눈물이 담긴 화이트보드.. 사실 이만한게 3개는 더 있었다 😭😭

B tree 개요

정의

B트리는 데이터를 정렬하여 탐색, 삽입, 삭제 및 순차 접근이 가능하도록 유지하는 트리형 자료구조이다.

B tree의 장점

B트리는 Balanced-Tree의 일종으로 어떠한 경우에도 트리의 균형이 유지된다.
균형이 유지된다는 것은 탐색에 있어 최악의 경우에도 시간복잡도가 O(lonN)을 유지한다는 것을 의미한다.

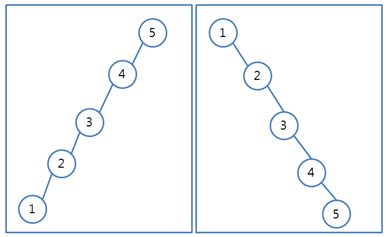
편향트리의 경우 최악의 경우 탐색할 때 O(N)의 시간이 걸리지만 균형트리를 유지하면 최악의 경우에도 O(logN)을 유지한다.

https://matice.tistory.com/8

B트리의 특징은 <INTRODUCTION TO ALGORITHMS, Thomas H.Cormen>의 서적의 내용에 따라 정의하였습니다

B tree의 특징

노드의 자료를 key, 노드의 자식을 child라고 한다면,

자료는 정렬된 상태로 저장된다.

차수를 t라고 했을 때, 노드의 key의 수는 최소값은 t-1개이고 최대값은 2*t-1개이다.(t-1 <= 키의 개수 <= 2t-1)

차수를 t라고 했을 때, 노드의 child의 수의 최대값은 2*t개이다.

차수는 2이상이어야한다.(t>=2)

노드의 key의 수가 n개라면 child의 수는 n+1개이다.

입력 자료는 중복될 수 없다.

B tree 구현

구현을 시작 하기 전에

B트리 구현을 시작하기 전에 자료조사를 하면서 굉장히 혼란스러웠다.

많은 자료들이 Bottom-up 방식으로 구현하는데 Bottom-up 논리로 삽입(insert)을 구현하는 방법은 명확했지만 같은 로직으로 삭제(delete)구현하는 방법은 굉장히 복잡했고 delete를 어떻게 구현해야할 지 충분히 이해가 가지 않았다.

결국 인터넷 자료 찾는 것을 멈추고 교과서를 펼쳤다. <INTRODUCTION TO ALGORITHMS, Thomas H.Cormen>라는 책은 1200페이지 번역체 양장본 교과서여서 좀처럼 손이 안갔는데 인터넷에서 정확한 자료를 찾기 힘들다는 판단을 하고 나니 믿을 것을 교과서 뿐이었다.

인터넷의 수 많은 자료들이 Bottom-up방식을 채택해서 논리를 펼친 것과는 달리 책은 Top-down 방식을 설명하고 있었다.

Top-down 방식의 핵심은 "절대 다시 루트 방향으로 되돌아가지 않을거야"

책의 논리를 이해할 수록 "답은 이거다!" 하는 생각이 들었고 우리 팀원들도 같은 마음이었을 것이다. 결국 책의 논리를 따라가며 B트리 구현을 완료했다. 이 곳에 책의 내용의 전부를 기록할 수는 없지만 핵심 내용을 중심으로 설명할 계획이다.

B tree 삽입

핵심 아이디어
: 루트에서부터 리프까지 길을 찾아 가면서 삽입되기 전까지 지나가는 모든 노드를 가득 차 있지 않게 만들면서 지나갈거야

삽입할 K가 들어갈 노드를 찾아갔는데 노드가 꽉 차있으면 노드의 중앙값을 부모에게 넘겨주면서 노드를 쪼개어(split) 키의 개수를 줄여야 한다.
쪼개고(split)나면 이제 K가 들어갈 공간이 생겼으니 K를 삽입해줄 수 있다.

하지만 여기서 Bottom-up 방식의 문제는 노드의 부모로 K를 보내야하는데 부모도 가득 차 있는 상태라면?
부모의 부모도 가득 차 있는 상태라면? 계속해서 루트를 향해 올라가야하는 일이 발생한다. 왔던 길로 되돌아가면서 쪼개는 작업을 해야하는 것이다.

하지만 리프를 향해 내려가면서 key의 개수가 2*t -1인 노드를 쪼개면서 들어가준다면 우리는 되돌아가는 작업을 하지 않아도 된다.

자, 이 트리에 17이 삽입된다고 생각해보자

노드가 가득 차 있지 않으면 그냥 해당 노드로 이동하고 재귀함수를 돌리면 된다.

해당하는 child로 들어와서 다음 노드를 바라보고 물어본다. 노드가 가득 차 있니?
노드가 가득 차 있기 때문에 해당 노드를 쪼개줘야한다.

Split() 함수를 실행시켜서 노드를 쪼개 준 후에 비로소 가려던 노드로 이동할 수 있다.

17이 들어가야할 리프노드를 찾았다. 노드의 key의 개수가 2*t - 1 보다 작기 때문에 바로 17을 삽입해준다.

B tree 삭제

핵심 아이디어
: 루트에서부터 리프까지 길을 찾아 가면서 삭제되기 전까지 지나가는 모든 노드를 빈곤하지 않게 만들면서 지나갈거야

삭제할 K가 들어갈 노드를 찾아갔는데 노드가 빈곤하면(노드의 key의 개수가 t-1개이면) 노드를 재배치(=빌려오기) 혹은 병합하여 키의 개수를 풍족하게 만들어줘야 한다.
재배치 혹은 병합하고나면 이제 K가 삭제되어도 노드가 사라지지 않기 때문에 K를 삽입해줄 수 있다.

먼저 삭제할 key가 리프노드에 있는 경우와 내부노드에 있는 경우로 나눠야 한다.

삭제할 key가 리프노드에 있는 경우를 먼저 살펴보자.

22를 삭제하러 가보자

루트 노드를 보니 빈곤하지 않으면 문제없이 해당 노드로 이동할 수 있다.(= 삭제할 노드가 해당 노드에 있더라도 문제없이 삭제할 수 있다). 해당 노드로 이동해서 k가 없으면 내려갈 노드를 선택해서 재귀함수를 돌린다.

가려는 노드의 key의 개수가 빈곤하면 해당 노드가 빈곤하지 않게 조치를 취해주고 내려가야한다.
조치에는 두 가지 방법이 있다.

왼쪽 형제와 오른쪽 형제 중 한명 이상이 풍족한 경우
- 풍족한 형제한테 key 하나를 빌려온다.
- 형제한테 key를 빌려오는 경우에는 반드시 부모를 거쳐서 빌려와야한다.
둘 다 빈곤한 경우
- 부모와 형제 노드와 해당노드를 병합해서 하나의 노드에 합친다.
- 이것이 가능한 이유는 빈곤하다는 것은 t-1개의 key를 가지고 있다는 것과 같기 때문에 (형제노드의 ket 개수) + (해당 노드의 key 개수) + (부모) = (t-1)+(t-1)+(1)을 하면 2t-1개의 key를 >가진 완전 풍족한 노드로 병합할 수 있다.

사진의 경우는 왼쪽 형제가 풍족한 상태이기 때문에 key를 빌려와야하는데 반드시 부모를 통해서 key 10을 부모에게 주고 key 20을 해당 노드에 추가해야한다.

형제에게 key를 빌려와서 이제 빈곤하지 않게되었고 22를 해당 노드로 이동한 후 재귀를 돌린다.

또 다시 다음으로 이동해야할 노드를 보니 key의 개수가 t-1 개이다(=빈곤하다ㅠㅠ). 혹시 풍족한 형제가 있나 봤더니 왼쪽 형제, 오른쪽 형제 모두 빈곤하다.
이 경우 우리는 병합을 해줘야한다.

형제노드와 부모노드를 해당노드에 병합해준 후

병합을 통해 비로소 해당 노드로 내려갈 수 있게 되었다. 22를 발견했으니 삭제해주면 된다.

삭제할 key가 내부노드에 있는 경우를 살펴보자.
삭제할 key가 내부노드에 있는 경우에는 데이터를 삭제하기 전에 대체해줄 데이터를 찾야한다.

대체할 데이터(k')는 오른쪽 노드의 제일 왼쪽 데이터(후행키) 혹은 왼쪽 노드의 제일 오른쪽 데이터(선행키)가 된다.
k'로 삭제할 데이터를 대체한 후에 다시 k'를 찾아가서 데이터를 지우면 내부노드 삭제가 완료된다.

고려해야할 부분 (root는 예외일 경우가 있다)

코드를 구현하면서 가장 계속 찜찜했던 부분이 root에 대한 부분이었다. 위의 로직에 따르면 사진의 첫번째 경우가 해결되지않았다.
이 부분에 대해 전처리를 해줌으로써 예외 케이스를 해결할 수 있었다.

예외 상황
루트는 예외적으로 key의 개수가 t -1개이고 오른쪽, 왼쪽 자식노드의 leaf 노드이면서 key의 개수가 모두 t-1 개일 때는 트리의 높이가 낮아진다.

void B_Plus_Tree_Delete(B_Plus_Tree* T, int k) {
	//Visual(T->root, 0);
	node* r = T->root;
	if ((r->n == 1 && r->leaf == FALSE) && ((r->child[0])->n == DEGREE - 1 && (r->child[1])->n == DEGREE - 1)) {
		node* y = r->child[0];
		node* z = r->child[1];
		if (y->leaf == TRUE) {
			for (int j = 0; j < DEGREE - 1; j++) {
				y->key[j + DEGREE - 1] = z->key[j];
			}
			y->n = 2 * DEGREE - 2;
			y->next = NULL;
			T->root = y;
			free(r);
			free(z);
			B_Plus_Tree_Delete_main(y, k);
		}
		else {
			y->key[DEGREE - 1] = r->key[0];
			for (int j = 0; j < DEGREE - 1; j++) {
				y->key[DEGREE + j] = z->key[j];
			}
			for (int j = 0; j < DEGREE; j++) {
				y->child[DEGREE + j] = z->child[j];
			}
			y->n = 2 * DEGREE - 1;
			T->root = y;
			free(r);
			free(z);
			B_Plus_Tree_Delete_main(y, k);
		}
	}
	else {
		B_Plus_Tree_Delete_main(r, k);
	}
	return;
}

B+ tree

정의

B tree의 변형 구조로 index노드과 순차 데이터 구조로 이루어진다. 순차 데이터 구조는 leaf노드를 연결리스트로 연결해놓은 형태이다.
데이터의 빠른 접근을 위해 내부 노드(index노드)는 인덱스의 역할만 하고 데이터는 leaf노드에만 저장되어있다.

장점

leaf 노드끼리 연결 리스트로 연결되어 있어서 탐색에 매우 유리하다.
인덱스된 순차 파일을 구성하는데 사용된다.

B tree 구현

B tree --> B+ tree에서 추가된 부분

node struct에 리프 노드일 경우 다음 리프 노드를 연결해줄 포인터(node*next)를 추가한다.

쪼개야할 노드가 리프 노드라면, Split될 때 분할된 오른쪽 노드에 부모로 올라간 데이터(중앙값)을 남겨둔다.

쪼개야할 노드가 내부 노드라면, B tree와 똑같이 Split해주면 된다.

B + tree 구현하기 전 고민한 부분

B+ tree 삭제를 구현하면서 가장 고민했던 부분은 index 노드의 값을 항상 리프노드의 0번째 인덱스로 유지시켜줘야할 지에 대한 부분이었다.
하지만 논의 끝에 index 노드는 leaf 노드를 찾아가는 길잡이 역할에만 충실하면 된다는 결론을 내렸다.

B+ tree 삽입 구현

삽입을 끝낸 후에는 리프 노드의 0번째 인덱스의 key들이 내부노드에 index노드로 길잡이 역할을 할 것이다.
이 트리 구조에서 데이터에 접근할 수 있는 주소를 가지고 있는 노드는 leaf 노드 뿐이다. index 노드의 key는 리프노드까지 찾아오는데 길잡이 역할을 할 뿐이지 실제 데이터와는 아무 상관이 없다.