저희 스터디가 이번에 그래프 알고리즘에 대해서 공부했습니다. 그 중에서 DFS/BFS에 대해서 알아봤습니다.
일단, 그래프는 우리가 흔히 일상생활에서 앱으로 버스와 지하철의 노선도를 확인할 있습니다. 그 앱에서 출발지와 목적지를 선택하여 최적의 경로를 알 수 있는데, 이런 프로그램 구현에 사용되는 것이 그래프 알고리즘입니다.
그래프는 정점과 간선으로 구성되어 있는 자료구조입니다.
정점은 아래의 이미지의 (1)에 있는 것 처럼 연결의 대상이 되는 개체 또는 위치를 의미하고, 노드(Node)라고도 불립니다. 그리고 간선은 정점을 연결한 선으로 위치 간의 관계를 나타냅니다.
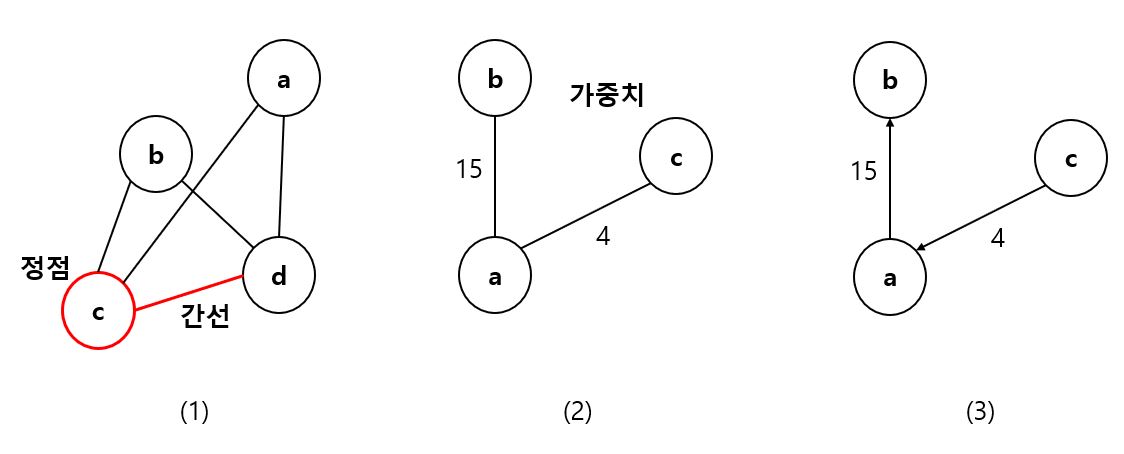
가중치 그래프라고 합니다. 간선마다 어떤 가중치 값을 할당한 그래프를 말합니다. 거기에 무방향 그래프입니다. 무방향 그래프는 간선에 화살표가 없고 따라서 양방향으로 서로 갈 수 있음을 의미합니다.
(3)의 그래프는 방향 그래프로 화살표 모양의 간선을 사용해서 갈 수 있는 방향을 표시합니다. 거기에 가중치 그래프이기도 합니다.
여기서, 연결 그래프는 그래프 내의 모든 정점들 서로 간에 갈 수 있는 경로가 존재하는 그래프를 의미합니다. 위의 이미지에서 (1)과 (2) 그래프를 말합니다.
하지만, 정점 쌍(Pair) 한 개라도 서로 갈 수 있는 길이 없으면 비연결 그래프입니다. 위 이미지의 (3)에서 정점 b에서 정점 a로 가는 길이 없기 때문에 비연결 그래프입니다.
위의 이미지에서 표현하지 않았지만 완전 그래프라는 것도 존재하는데, 이는 모든 정점들 사이에 1:1로 직접 연결된 간선을 지닌 그래프를 말합니다.
추가적으로, 사이클(Cycle)은 정점 V에서 출발하여 정점 V로 되돌아오는 경로를 말합니다.
여기서 그래프와 트리가 어떤 차이가 있는지 궁금하실 수 있습니다.
트리는 그래프 중에 속한 특별한 종류라고 볼 수 있습니다.
위에서 설명한 사이클이 없는 그래프를 비순환 그래프라고 하는데, 트리는 사이클이 없는 비순환 그래프입니다. 반면에, 그래프는 사이클도 가능하고, 비순환 그래프도 될 수 있습니다.
또한, 그래프는 방향 그래프, 무방향 그래프 둘다 존재할 수 있는데, 트리는 방향 그래프만 존재합니다.
하지만, 그래프는 루트 노드가 존재하지 않고, 부모-자식 개념도 존재하지 않습니다. 그 와는 반대로 트리는 루트 노드가 존재하고, 부모-자식 관계가 존재합니다.
이 그래프를 탐색하는 알고리즘에는 크게 DFS와 BFS가 존재합니다.
DFS(Depth First Search)
깊이 우선 탐색이라고 합니다.
그래프에는 여러 갈래의 길이 있을 수 있는데, DFS의 이름이 의미하듯이 한 길을 깊이 파고드는 것입니다.
시작 정점에서부터 최대한 깊숙히 들어가서 확인한 뒤 다시 돌아가 다른 노드로 탐색하는 방식으로, 모든 곳을 방문하고할 때, 이 방식을 사용합니다.
스택(Stack) 또는 재귀함수로 구현합니다.
BFS(Breadth First Search)
너비 우선 탐색이라고 합니다.
DFS가 한 사람에게 연락을 취하는 방식이라면, BFS는 자신에게 연결된 모든 사람에게 연락을 취하는 방식입니다.
즉, 시작 정점에서부터 인접한 정점을 먼저 탐색하는 것입니다.
주로 두 정점 사이에서 최단 경로를 찾고 싶을 때, 이 방법을 사용합니다.
큐(Queue)를 이용하여 구현합니다.
그래프 알고리즘은 코테에 자주 출제된다고 알려져있고, 그 만큼 어렵기 때문에 이 그래프 알고리즘에 적응하기 위해 스터디에서 DFS/BFS 개념에 대해 알고있으면 풀기 쉬운 알고리즘 문제부터 풀어봤습니다.
개념문제는 풀어볼만 했지만, 백준에서 머리 좀 써야하는 응용 문제에서 벽을 느꼈습니다.
다른 분 것을 참고하여 풀었는데, 코드는 이해했지만 이것을 실제로 코테 문제로 나온다면 도저히 풀 자신이 없다고 생각했습니다. 이 문제는 잊을 때 쯤에 꼭 다시 한 번 풀어봐야겠다고 느꼈습니다.
