[AIFFEL] 22.Feb.18 - Information_Theory

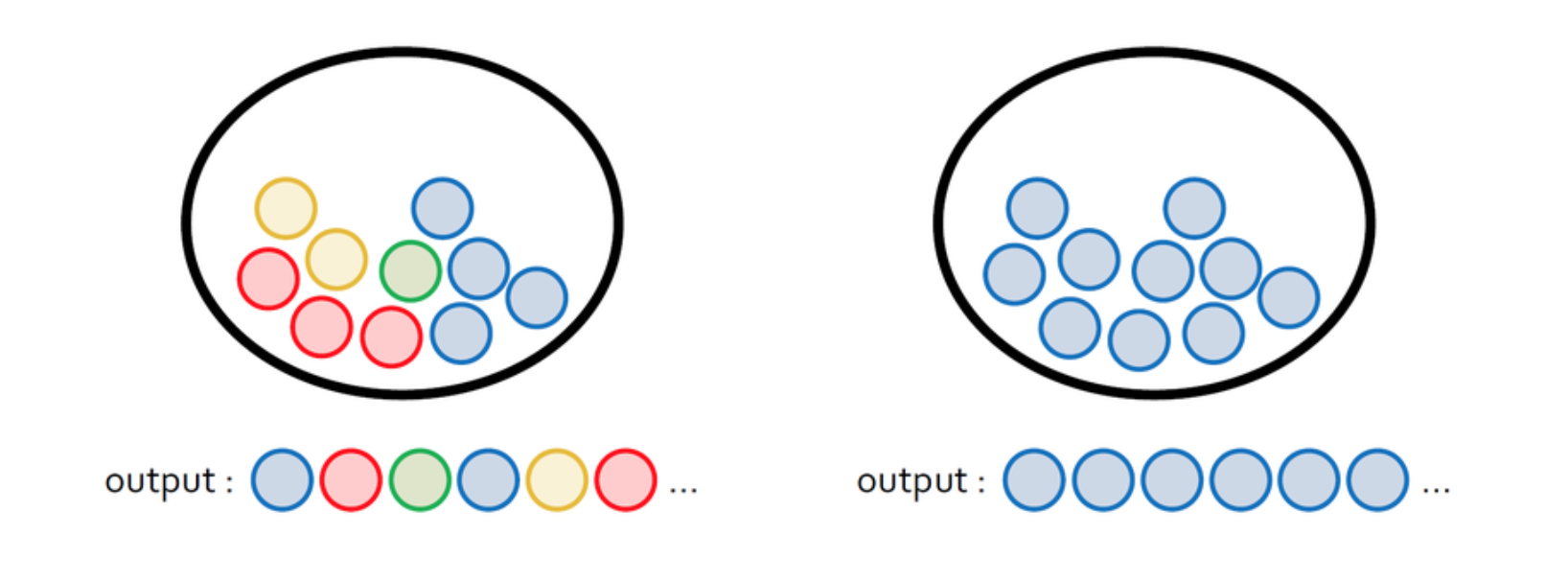
• discrete variable이 여러 개 있을 때 거기서 얻을 수 있는 정보량의 공식인데

  • 
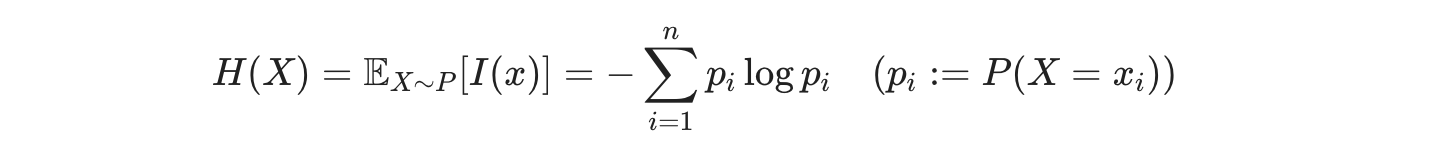
  • 직관적으로 이해해보고자 한다면,
  • 하나당 정보량은 $logP(x)$이지만,
  • 그것이 여러 개가 될 경우 비율을 맞춰주기 위해 각각의 확률로 곱해주는 것인 것 같다.(결과적으로 총합 1의 비율이 되게)
  • 그리고 서로 간의 확률이 균등해질 때 정보량은 제일 커진다.(아마 0.9, 0.1 이렇게 있는 것보다 0.5, 0.5 이렇게 있는 게 더 큰가보다. 즉, 0.9 1개의 로그 변환 값보다 0.5 로그 변환 값 여러 개의 힘이 더 큰 것 같다.)

• countinous variable 일 경우에는 위의 식에서 더해주는 것을 적분, 곱해주는 각각의 확률을 변화량(dx)로 바꾸면 된다.

• 머신러닝 모델은 크게 두 종류이다.

  • 우선 결정 모델(discriminative model)
    • 데이터 분포 신경 안 씀(모델링 안 함)
    • 그냥 결정 경계(decision boundary)만 학습함
  • 생성 모델(generative model)
    • 데이터와 모델을 그려봐서 나오는 여러 확률 분포 중 제일 좋은(?) 것 사용
    • 베이즈 이론(Bayes' Theorum) 사용
    • 그런데 이런 확률 지표들을 비교하기 위해 KL-Divergence를 사용

• KL-Divergence

  • 결론적으로 확률 분포들을 비교하게 해준다. 어떻게?
  • 
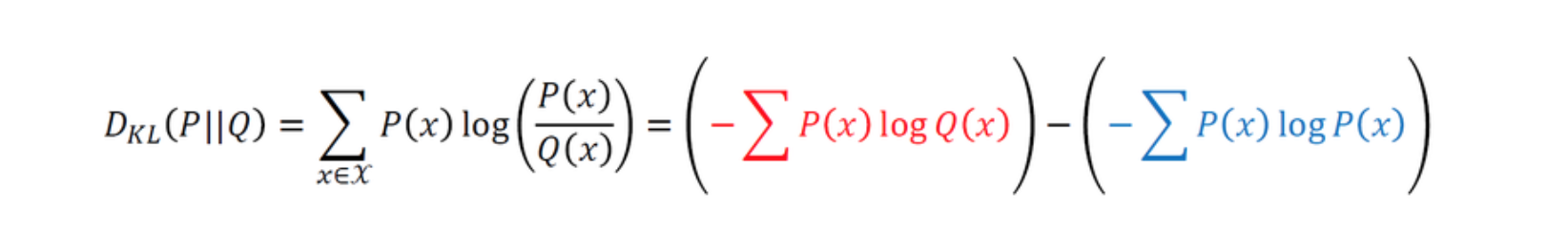
  • 파랑색은 실제 데이터의 분포에 대한 정보량
  • 빨강색은 예측 값의 분포에 대한 정보량
  • 이 차이를 제일 적게 가지는(실제 분포 정보량에서 예측 값의 정보량을 빼줌) $Q(x)$의 분포를 찾는 것
  • 그런 모델을 찾으려 하는 게 생성 모델이다.
  • 그런데 저기서 $Q(x)$의 정보량을 나타내는 것은 사실 cross entropy
  • 그리고 $P(x)$의 정보량을 나타내는 건 entropy
  • 그래서 식으로 나타내면
  • entropy에서 cross entropy를 뺀 그 차이가 바로 KL-divergence 값

• Cross Entropy Loss

  • 분류 문제에서 loss function으로 많이 씀
  • 이진 분류일 때는 logistic regression 함수를 써서 실제 데이터와 예측 값의 차이를 계산하지만
  • 많아지면 logistic regression의 확장판(?)인 softmax를 사용
  • 역시나 softmax를 사용해서 나온 예측 값의 분포와 실제 데이터 분포의 차이를 계산하는 게 loss function의 역할

임종관 교수님 AI 진로 관련 Q&A 시간

코딩

• 데이터사이언스만 한다면 python
  • python은 빠르게 직관적으로 실험할 수 있어서 씀
• 다른 IT도 한다면 C를 알아야 함
• 특히 CV하려면 C는 나중에라도 알아야 할 것
  • C++, C# 굳이 차이를 두진 않고, 업계에서는 하나 알면 다 할 줄 안다고 봄

수학

• 통계, 선형대수 강조하심
• 그리고 코드로 구현할 줄 알아야(sklearn 같은 거 말고)