스택 & 큐 & 이진탐색

💡 큐

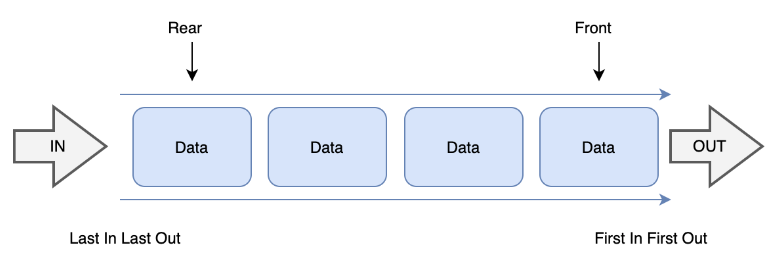
• 선입선출 FIFO → 제일 먼저 들어간 값이 제일 먼저 나온다.
• 백준 2164 문제
• 선언

  // 1. 일반 큐 자료형 선언
  Queue<자료형> 이름 = new LinkedList<>();
  
  // 2. 오름차순 우선순위 큐 선언 (값의 크기 순서로 출력 -> 오름차순)
  PriorityQueue<자료형> 이름 = new PriorityQueue<>();
  
  // 3. 내림차순 우선순위 큐 선언 (값의 크기 순서로 출력 -> 내림차순)
  Queue<자료형> 이름 = new LinkedList<>(Collections.reverseOrder());

• 관련 함수
  • add() → 값 추가
  • peek() → 값 확인
  • poll() → 값 출력 후 삭제
  • element() → peek 과 비슷, 하지만 값이 없을 경우 오류 출력
  • size() → 자료구조의 크기 출력
  • isEmpty() → 값 비어있는지 확인 true/false

2. 문제

(1) 백준 2164

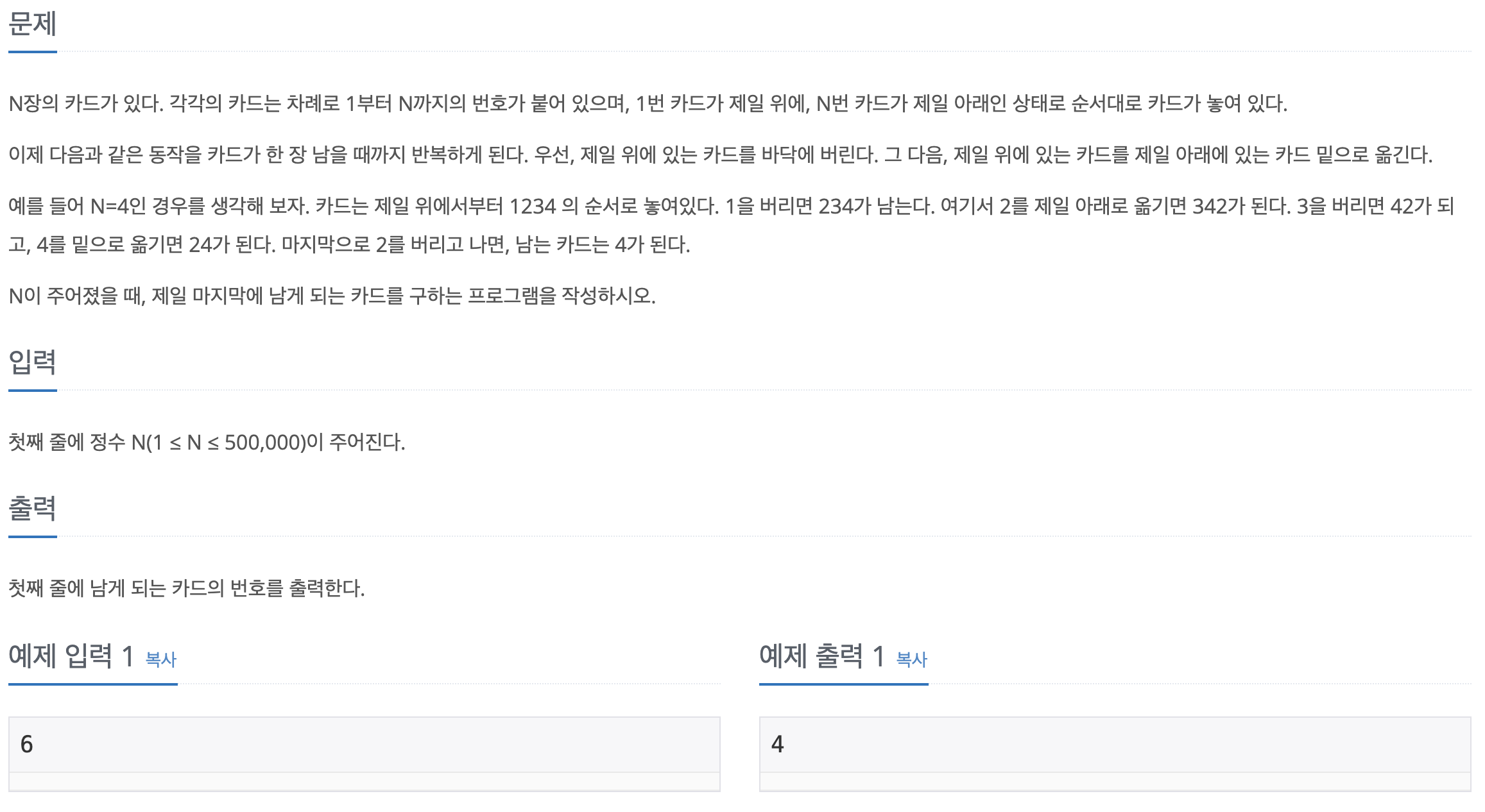
• 문제 이해

  • 입력 받은 값을 통해 큐 자료구조에 1-N까지의 값을 넣고
  • 맨 위의 값(제일 먼저 넣은 값)을 하나 뺀 뒤, 그 다음 값을 빼서 처음으로 값을 넣는다.
  • 마지막 하나 남은 값을 출력한다.

• 슈도 코드

  1. int N 입력 받고 초기화
  2. 큐 자료구조에 1~N 만큼의 값 넣기
  3. 큐 자료구조에 한 개의 값만 남을 때까지,
     1. poll() 로 맨 위 값 빼기
     2. temp 에 다음 값 저장
     3. 해당 다음 값 poll() 로 뺀 뒤
     4. 그 temp 값을 add() 로 맨 뒤에 추가
  4. 남은 값 하나 출력

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));

        int n = Integer.parseInt(bf.readLine());

        Queue<Integer> queue = new LinkedList<>();

        // 큐에 값 저장
        for (int i = 1; i <= n; i++) {
            queue.add(i);
        }

        while (queue.size() > 1) {
            queue.poll();
            int temp = queue.element();
            queue.poll();
            queue.add(temp);
        }
        System.out.println(queue.element());
    }
}

---

💡 스택

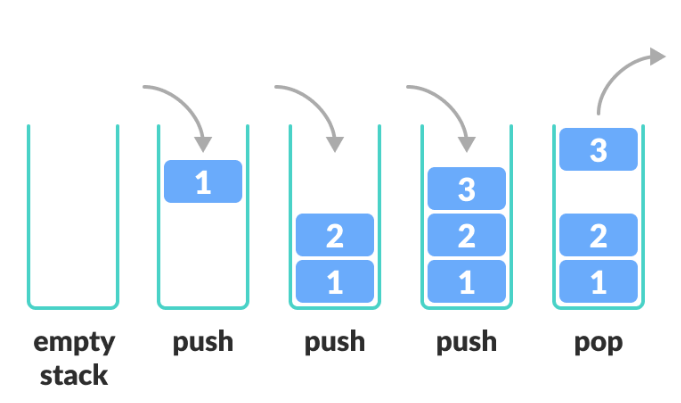
• 후입선출 LIFO → 제일 마지막에 넣은 값이 먼저 나온다.

• 맨 위에 있는 값을 top 이라 한다.

• 선언

  Stack<자료형> 이름 = new Stack<>();

• 백준 1874 문제 (스택으로 오름차순 수열 만들기)

• 관련 함수

  • push()→ 맨 위 top 에 값 추가
  • pop() → 맨 위 top 값 출력 후 빼기

문제

(1) 백준 1874

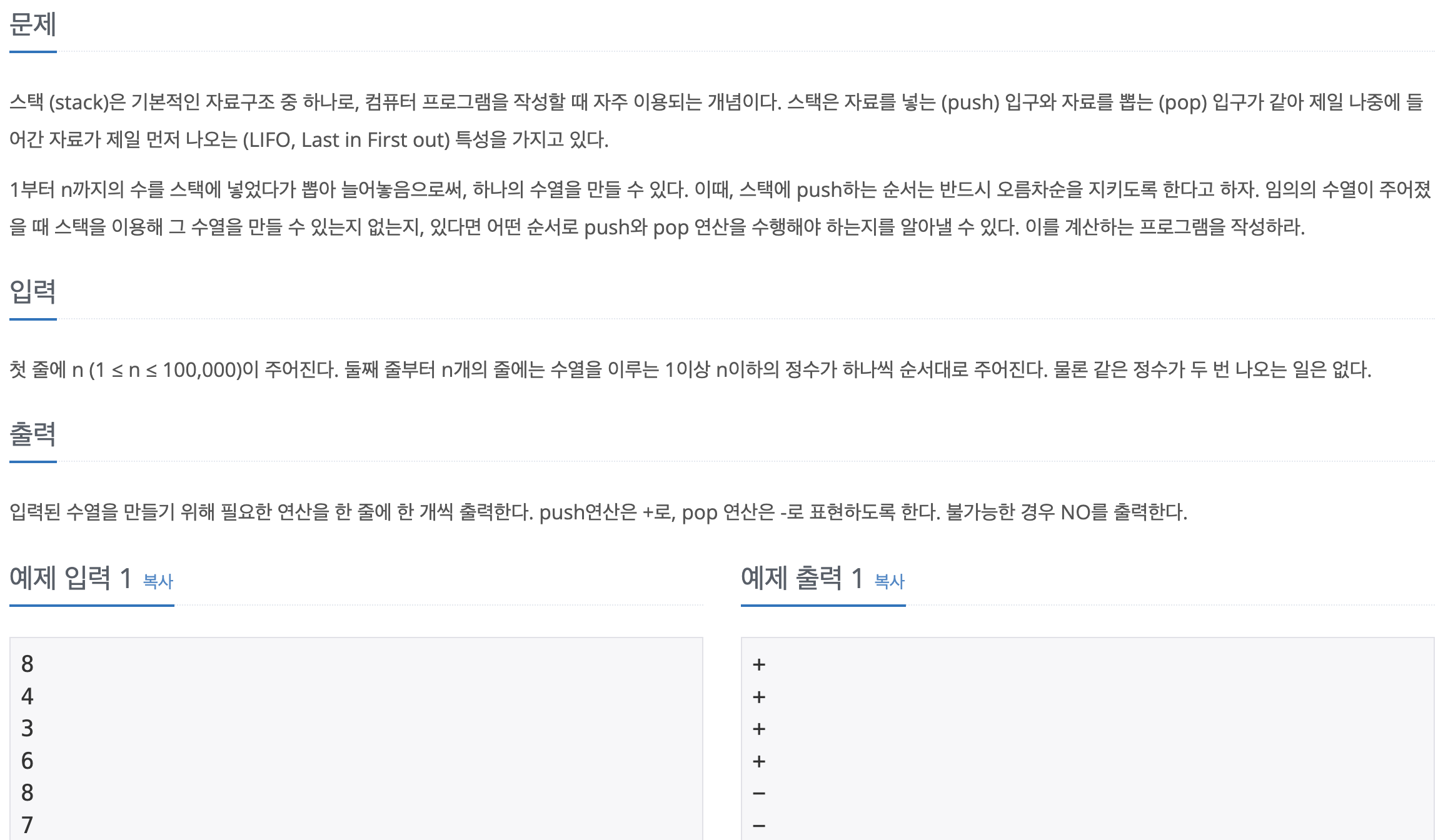
• 문제이해
  • N 크기의 순열을 입력 받아 스택에 넣은 뒤 출력이 가능한지 확인할 수 있는 문제이다.
  • 스택 구조로 넣은 뒤 출력이 가능하다면 push → + , pop → - 를 출력한다.
  • 스택 구조가 허용되지 않을 경우 NO 를 출력한다.
• 슈도 코드

  1. N 을 입력 받아 해당 크기만큼 순열을 입력받는다, arr 배열에 순열 저장.

  2. 답 출력을 위한 StringBuffere sf 초기화

  3. Stack 자료구조를 생성하고, num = 1 초기화 (오름차순을 위함)

  4. if( 순열의 값이 num 보다 크거나 같다면 )

     1. 같아질 때까지 stack에 num++ 값 추가
     2. sf에 “+” 추가
     3. 같아졌다면 pop으로 값 출력
     4. sf에 “-” 추가

     else { if (num보다 작다 )→ pop 을 통해 값 꺼냄, “NO” 출력

     else { num == 순열값 이니까, sf에 “-” 추가

     e. StringBuffer 출력

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));

        int n = Integer.parseInt(bf.readLine());
        int[] arr = new int[n];
        boolean result = true;

        for (int i = 0; i < n; i++) {
            int temp = Integer.parseInt(bf.readLine());
            arr[i] = temp;
        }
        StringBuffer sf = new StringBuffer();
        Stack<Integer> stack = new Stack<>();
        int num = 1;
        for (int i = 0; i < arr.length; i++) {
            int su = arr[i];
            if (su >= num) {
                while (su >= num) {
                    stack.push(num++);
                    sf.append("+\n");
                }
                stack.pop();
                sf.append("-\n");
            } else {
                int a = stack.pop();
                if (a > su) {
                    System.out.println("NO");
                    result = false;
                    break; 
                } else {
                    sf.append("-\n");
                }
            }
        }
        if(result) System.out.println(sf.toString());
    }
}

(2) 백준 17298

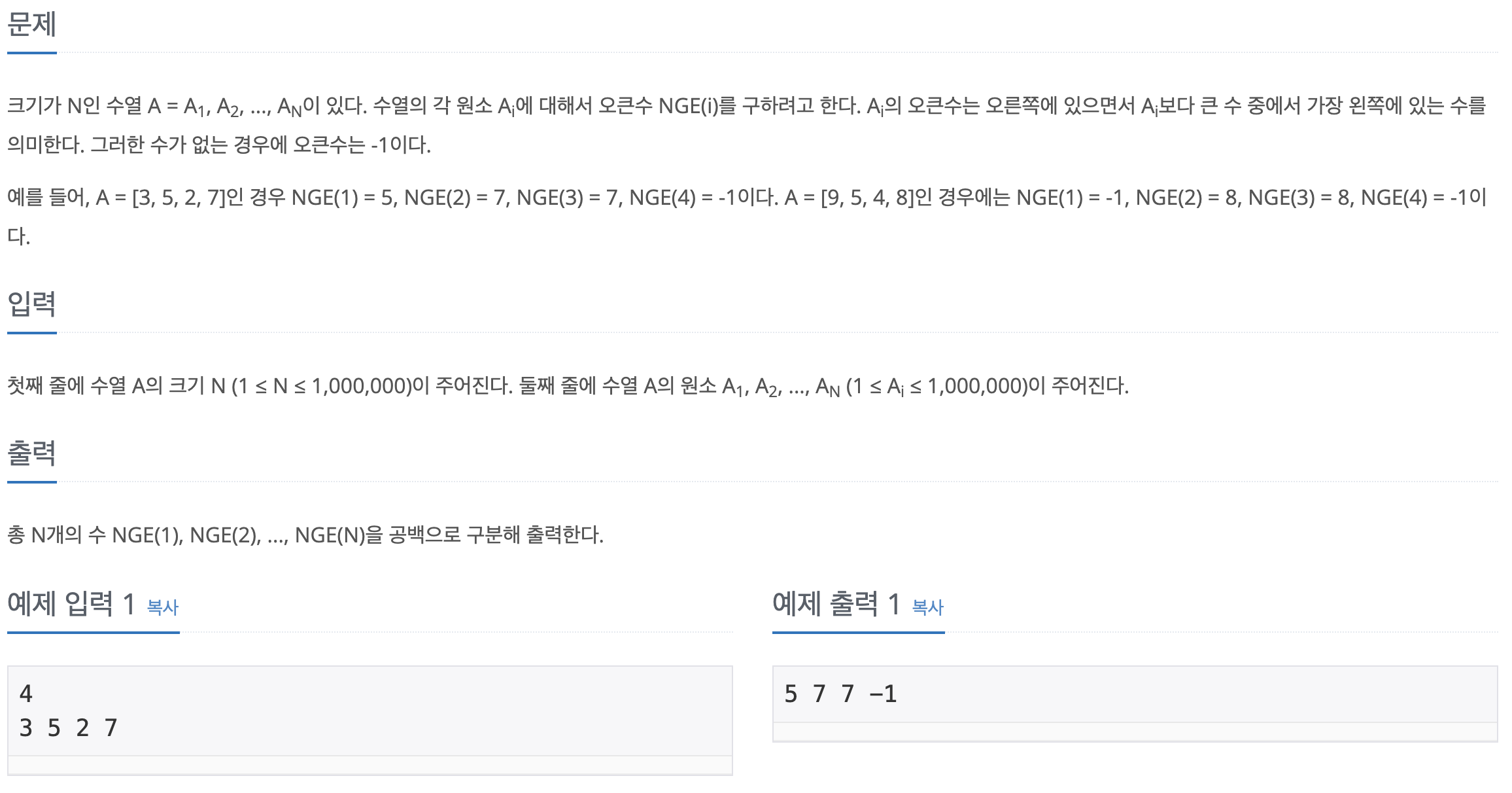
• 슈도 코드
  1. int N 입력, 초기화
     1. stack 초기화, arr에 먼저 입력값 저장
  2. N 번 반복으로 stack에 저장
  3. int max = 0 으로 초기화
  4. for (arr 크기 만큼)
     1. while ( stack.size > i + 1)
        1. int temp = stack.pop()
           1. if (arr[i] < max) { max = temp }
     2. for ( i+1 ~ arr 크기만큼 )
        1. stack.add(arr[i+1])
• 오답 코드

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));

        int N = Integer.parseInt(bf.readLine());
        Stack<Integer> stack = new Stack<>();

        StringTokenizer st = new StringTokenizer(bf.readLine());
        int[] arr = new int[N];
        for (int i = 0; i < N; i++) {
            int a = Integer.parseInt(st.nextToken());
            arr[i] = a;
            stack.add(a);
        }

        for (int i = 0; i < arr.length; i++) {
            int max = 0;
            while (stack.size() > i + 1) {
                int temp = stack.pop();
                if (arr[i] < temp) {
                    max = temp;
                }
            }
            if (max != 0) {
                System.out.print(max + " ");
            } else {
                System.out.println("-1 ");
            }

            for (int j = i + 1; j < arr.length; j++) {
                stack.add(arr[j]);
            }
        }
    }
}

이와 같이 풀었으나 시간 복잡도가 N제곱이라 시간 초과로 실패하였다.

• 정답인 코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Stack;
import java.util.StringTokenizer;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));

        int N = Integer.parseInt(bf.readLine());
        Stack<Integer> stack = new Stack<>();
        int[] arr = new int[N];
        int[] nge = new int[N]; // 오큰수를 저장할 배열

        StringTokenizer st = new StringTokenizer(bf.readLine());
        for (int i = 0; i < N; i++) {
            arr[i] = Integer.parseInt(st.nextToken());
        }

        // 오큰수 계산
        for (int i = 0; i < N; i++) {
            while (!stack.isEmpty() && arr[stack.peek()] < arr[i]) {
                nge[stack.pop()] = arr[i];
            }
            stack.push(i);
        }

        // 남은 스택에 대해 오큰수가 없는 경우 -1로 처리
        while (!stack.isEmpty()) {
            nge[stack.pop()] = -1;
        }

        // 결과 출력
        for (int i = 0; i < N; i++) {
            System.out.print(nge[i] + " ");
        }
    }
}

---

💡 이진탐색

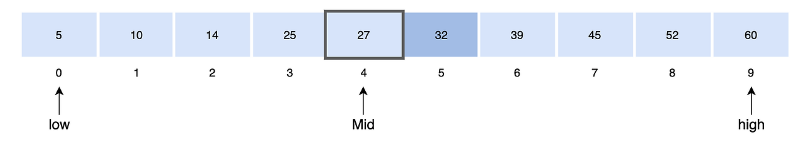
이진 탐색은 중간값을 계속 찾아 나아가는 방식이다. 위 배열처럼 배열 값 중 중간 값을 찾고 찾고자 하는 값을 찾아간다.

예를 들어 10을 찾고자 할 때
1. 중간 값인 27을 기준으로 왼쪽과 오른쪽 두 개의 노드가 생김
2. 찾고자 하는 값인 10이 왼쪽 노드에 있으므로 왼쪽에서 중간 값을 찾음
이와 같은 과정을 10이 나올 때까지 반복한다.

구현

public static int binarySearch(int[] arr, int target) {
        int left = 0;
        int right = arr.length - 1;

        while (left <= right) {
            int mid = left + (right - left) / 2;

            // 중간 요소가 타겟과 같은지 확인
            if (arr[mid] == target)
                return mid;
            // 중간 요소보다 타겟이 작으면 왼쪽 부분 탐색
            else if (arr[mid] < target)
                left = mid + 1;
            // 중간 요소보다 타겟이 크면 오른쪽 부분 탐색
            else
                right = mid - 1;
        }

        // 탐색 실패 시 -1 반환
        return -1;
    }