그리디 알고리즘

💡 그리디 알고리즘이란?

현재 상태에서 볼 수 있는 선택지 중 최선의 선택을 하는 알고리즘.
시간복잡도는 우수하나 항상 최적의 해를 보장하지 못한다는 단점이 있음.

항상 최선의 선택을 고른다.
다만 최종 결과의 최적해를 보장하지 못한다.
그러므로 최적의 해가 나올 수 있는 조건의 문제에서만 사용한다.

---

최적의 해가 나올 수 있는 조건?

만약, 서울에서 대전을 거쳐 부산을 가는 가장 빠른 경로를 선택한다고 가정해보자.

서울 ~ 대전의 경로에서 가장 빠른 경로는 1번 경로이다. 이 1번 경로를 간다고해서 대전 ~ 부산의 경로에 영향을 미치지 않는다.

근데 만약, 아래와 같다면 말이 달라진다.

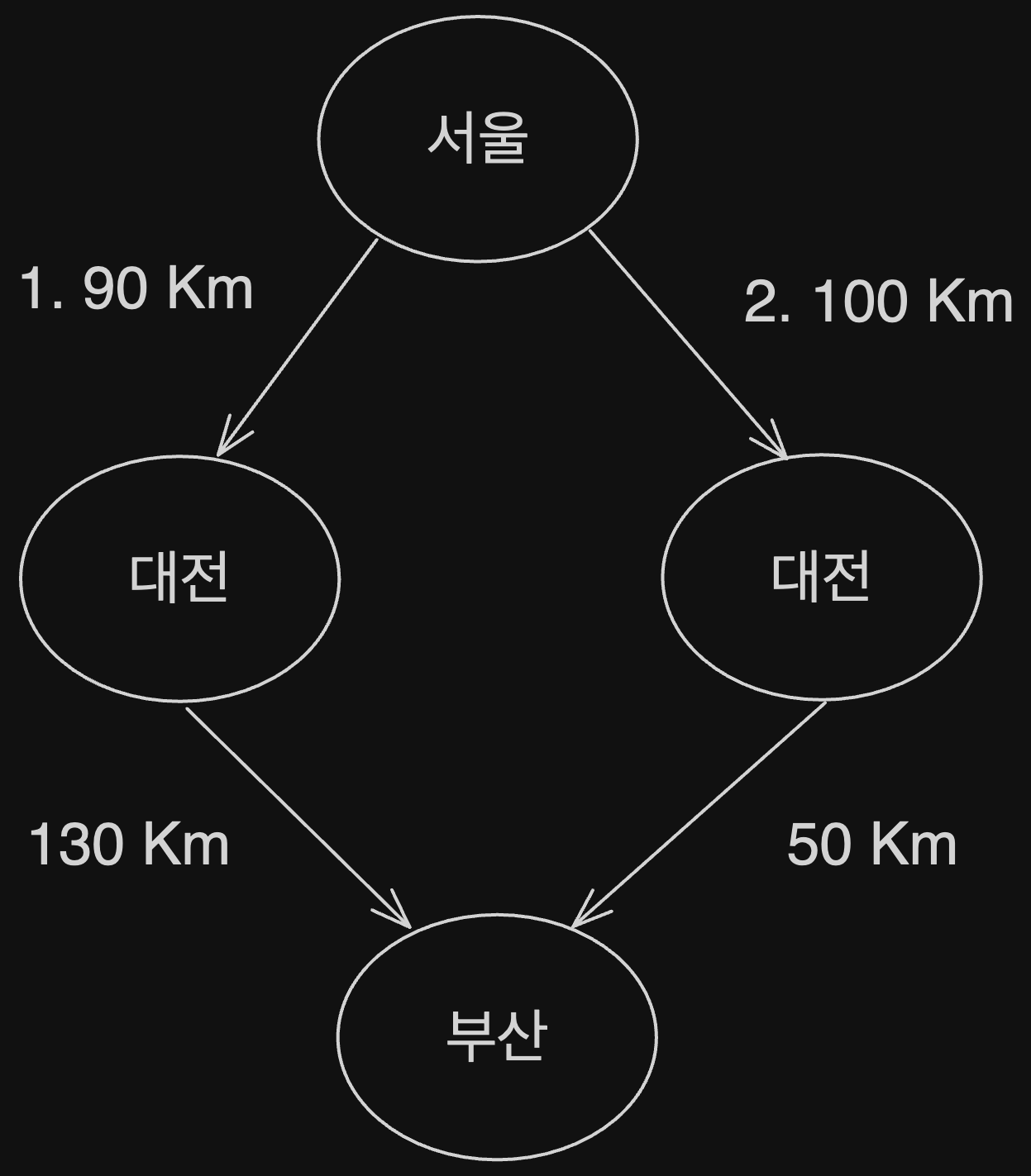
서울에서 대전을 갈 때 1 번 경로가 보다 빠르다고 선택했을 경우 최종적인 결과는 최적의해를 만족하지 못한다. 이러한 특징으로 그리디 알고리즘은 항상 최적의 해를 보장하지 않는다는 것이며, 코딩테스트에서 사용할 때 유심히 확인하고 사용하자

• 결론적으로 그리디 알고리즘에서 최적의 해가 나올수 있는 조건은 고려하는 상황의 결과 값이 이후의 결과값과 영향이 가지 않아야 한다. (서울~대전의 경로가 대전~부산의 경로에 영향이 가지 않아야 함)

---

대표적인 그리드 알고리즘 구현 문제

N 개의 동전이 주어졌을 때 K 원을 구하는 최소한의 동전 조합

만약 100, 200, 300, 500 의 동전이 있고, 최소한의 조합으로 2700원을 구한다면 어떻게 구할까?
일단, 제일 큰 동전부터 사용하는 것이 최적의 해를 구하는 방법이다.
500원을 먼저 사용한다면 5개의 동전으로 2500원을 만들고, 이후 200원의 동전 1개로 2700원을 만들어
총 6개의 동전이 최소한의 동전 조합이 된다.

사용자에게 동전에 대한 정보와 K를 입력받아 최소한의 동전 조합을 구하는 코드는 아래와 같다.

public class Main {

	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st = new StringTokenizer(br.readLine());
		
		int N = Integer.parseInt(st.nextToken()); // 동전의 개수
		long K = Integer.parseInt(st.nextToken()); // 원하는 값 K
		int[] arr = new int[N]; // 동전을 담을 배열
		
        // 배열에 입력된 동전 정보 저장 (동전은 오름차순으로 입력됨)
		for (int i = 0; i < N; i++) {
			arr[i] = Integer.parseInt(br.readLine());
		}
		
        // 동전의 개수를 위한 변수
		int count = 0;
		
        // K와 계속 비교해 가면서 실행
		while(K > 0) {
        	// 제일 큰 동전부터 사용
			for (int i = N-1; i >= 0; i--) {
				if (arr[i] <= K) {
					count += K / arr[i];
					K %= arr[i];
				}
			}
		}
		System.out.println(count);
	}
		
}