평범한 배낭
https://www.acmicpc.net/problem/12865
소스코드
static int [][] dp,items;
static int N,K;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine()," ");
N =Integer.parseInt(st.nextToken());
K =Integer.parseInt(st.nextToken());
items= new int[N][2];
for(int i = 0 ; i < N ;i ++) {
st = new StringTokenizer(br.readLine());
items[i][0] = Integer.parseInt(st.nextToken());
items[i][1] = Integer.parseInt(st.nextToken());
}
System.out.println(solution(items ,N,K));
}
static int solution(int [][] items,int N, int K) {
dp = new int[N + 1][K + 1];
for (int i = 0; i < N; i++) {
for (int j = 1; j <= K; j++) {
if (items[i][0] > j) {
dp[i + 1][j] = dp[i][j];
}
else {
dp[i + 1][j] = Math.max(dp[i][j], dp[i][j - items[i][0]] + items[i][1]);
}
}
}
return dp[N][K];
}
생각할 것
- dp 배열에 무엇을 값으로 담아 줄것인지
- 무게가 더 나간다면 이전의 무게를 dp에 담는다.
- 무게가 wieght <= j 넘어가지 않는 최대 값일 때
dp[i + 1][j] = Math.max(dp[i][j], dp[i]j - items[i][0]] + items[i][1]);
참고
https://loosie.tistory.com/370
============================================================
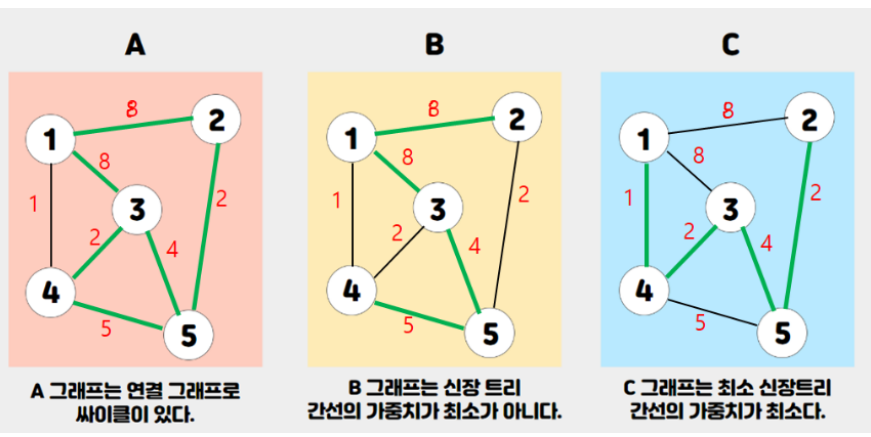
최소 비용 신장트리란?
📍 Minimum Spanning Tree의 약자로 '최소 연결 부분 그래프'를 의미한다.
📍 정점 N개를 가지는 그래프에서 (N - 1)개의 간선을 연결해야 한다.
📍 연결한 간선의 가중치 합이 가장 최소가 되는 그래프
📍 모든 정점이 연결되어야 하나, 싸이클이 되면 안된다.
정복자
https://www.acmicpc.net/problem/14950
소스코드
main
static int n,m,t;
static Node [] data;
static int [] parents;
public static void main(String[] args) throws IOException {
BufferedReader br= new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine()," ");
n = Integer.parseInt(st.nextToken());
m = Integer.parseInt(st.nextToken());
t = Integer.parseInt(st.nextToken());
data= new Node[m];
for (int i = 0; i < m; i++) {
st= new StringTokenizer(br.readLine()," ");
int A = Integer.parseInt(st.nextToken());
int B =Integer.parseInt(st.nextToken());
int weight = Integer.parseInt(st.nextToken());
data[i] = new Node(A,B,weight);
}
Arrays.sort(data);
parents = new int[n+1];
mst(data);
}
mst
static void mst(Node [] data){
long ret =0;
int cnt = 0;
for (int i = 0; i <n+1 ; i++) {
parents[i] =i;
}
for (Node edge: data) {
if(find(edge.from)== find(edge.to)){
//시작점과 끝점이 같으면 지나간다.
continue;
}
union(edge.from, edge.to);
ret += edge.weight + (cnt*t) ;
// 계속 가중치를 더해주는데
//한번 점령할때마다 t만큼 비용이 증가
cnt++;
}
System.out.println(ret);
}union & find
public static void union(int a, int b){
int aP=find(a);
int bP =find(b);
if(aP != bP){
parents[aP] =bP;
}
}
public static int find(int a){
if(a == parents[a]){
return a;
}
return parents[a] = find(parents[a]);
}크루스칼 알고리즘
- 간선의 가중치를 오름차순으로 정렬한다.
- 정렬된 간선 중에서 순서대로(가중치가 낮은 순으로) 간선을 조회한다.
2-1. 간선을 선택하게 될 때, 사이클이 형성된다면 다음 간선으로 넘어간다.
2-2. 사이클이 형성되지 않는다면 해당 간선을 선택한다.- 정점의 개수가 N일때, N-1만큼 간선을 뽑았다면 반복문을 종료한다.
- cycle 형성여부를 Union & Find 연산으로 판단 .
참고
https://born2bedeveloper.tistory.com/29
============================================================
최소 스패닝 트리
https://www.acmicpc.net/problem/1197
소스 코드
Kruskal
Kruskal MAIN
static class Node implements Comparable<Node>{
int start ;
int end;
int weight;
public Node(int start, int end, int weight){
this.start = start;
this.end=end;
this.weight =weight;
}
@Override
public int compareTo(Node o) {
return weight -o.weight;
}
}
static int V ,E;
static int [] parents;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
V =Integer.parseInt(st.nextToken());
E =Integer.parseInt(st.nextToken());
parents = new int[V+1];
for (int i = 0; i < V+1; i++) {
parents[i] = i;
}
PriorityQueue<Node> pq = new PriorityQueue<>();
for (int i = 0; i < E; i++) {
st= new StringTokenizer(br.readLine()," ");
int start =Integer.parseInt(st.nextToken());
int end =Integer.parseInt(st.nextToken());
int weight =Integer.parseInt(st.nextToken());
pq.add(new Node(start,end,weight));
}
int total=0;
while(!pq.isEmpty()){
Node cur= pq.poll();
if(find(cur.end) == find(cur.start)){
continue;
}else{
union(cur.end,cur.start);
total += cur.weight;
}
}
System.out.println(total);
}UNION & FIND
public static int find(int x){
if(parents[x] == x){
return x ;
}
return parents[x] = find(parents[x]);
}
public static void union(int x, int y){
x= find(x);
y= find(y);
if(x != y){
parents[y] = x;
}
//연결된 애들 값을 다 최솟값으로 고정
}
PRIM
prim Main
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int v = Integer.parseInt(st.nextToken());
int e = Integer.parseInt(st.nextToken());
list = new ArrayList[v+1];
visited = new boolean[v+1];
for(int i=1; i<v+1; i++) {
list[i] = new ArrayList<>();
}
for(int i=0; i<e; i++) {
st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
int w = Integer.parseInt(st.nextToken());
list[a].add(new Node(b,w));
list[b].add(new Node(a,w));
}
prim(1);
System.out.println(total);
}prim Fuc
static void prim(int start) {
PriorityQueue<Node> pq = new PriorityQueue<>();
pq.add(new Node(start,0));
while(!pq.isEmpty()) {
Node p = pq.poll();
int node = p.to;
int weight = p.value;
if(visited[node]) continue;
// 선택한 간선의 정점으로부터 가장 낮은 가중치 갖는 정점 선택
visited[node]= true;
total += weight;
for(Node next : list[node]) {
if(!visited[next.to]) {
pq.add(next);
}
}
}
}
생각 할 것
📍 프림 알고리즘은 visited 배열을 업데이트 해주면서 간선의 가중치를 더해준다.
📍 크루스칼 알고리즘은 union & find 함수를 통해 cycle이 형성되는지 확인하고 아니라면 가중치를 더해준다.