
GRAPH
Graph
What is graph?
- 그래프는 (Node, Edge)의 튜플로 표현되며 이때 Node를 Vertex라고도 함
- Node: 노드
- Edge: 연결
- Undirected graph: 노드들끼리 방향성이 존재하지 않는 그래프
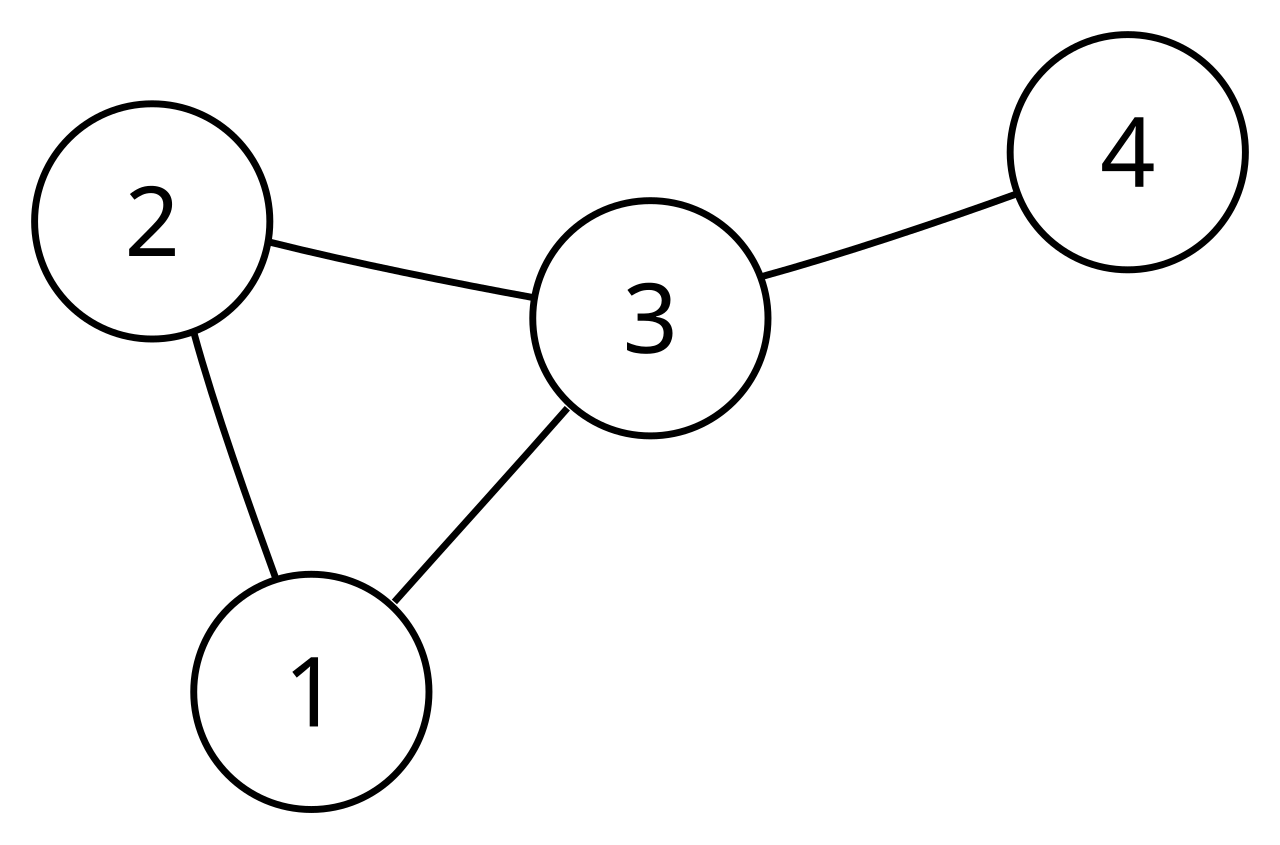
- Directed graph: Edge끼리의 방향성이 존재하는 graph

- Tree: Graph의 특이 케이스 중 하나
.svg/220px-Tree_(computer_science).svg.png)
Terminology
- Adjacent node: edge로 연결된 이웃 노드
- Path: node A에서 node B로 갈 때 지나가는 node들의 집합 (순서를 가짐)
- Complete graph: 어떤 node 쌍을 골라도 edge가 존재하는 graph
- undirected일 경우 연결만 존재하면 됨
- nC2개의 edge 존재 n * (n-1) / 2
- Directed일 경우 양방향으로 존재
- nP2개의 edge 존재 n * (n-1)
- undirected일 경우 연결만 존재하면 됨
- Weighted graph: edge마다 weight 존재해서 중요도를 다르게 부여한 graph
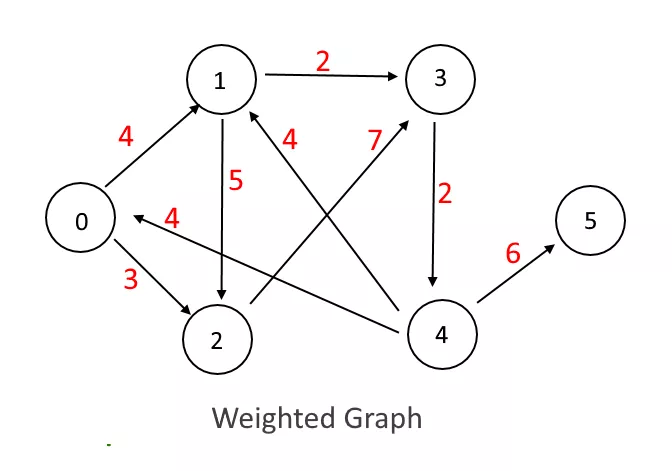
Implementation: Adjacency Matrix
- 2차원 배열로 그래프의 연결 관계를 표현하는 방식
- undirected graph에만 사용 가능
- Vertices: Vertex에 해당하는 index를 알려 주는 1차원 배열
- Adjacency Matrix: Vertex끼리의 edge 존재 유무와 weight를 알려 주는 2차원 배열
- Array Based이기 때문에 충분한 크기를 설정해 둬야 함
- Vertices의 index를 정렬해 놓으면 Searching 시간을 줄일 수 있음
- Sorted인 경우 이진 탐색 O(logN), Unsorted인 경우 완전 탐색 O(N)
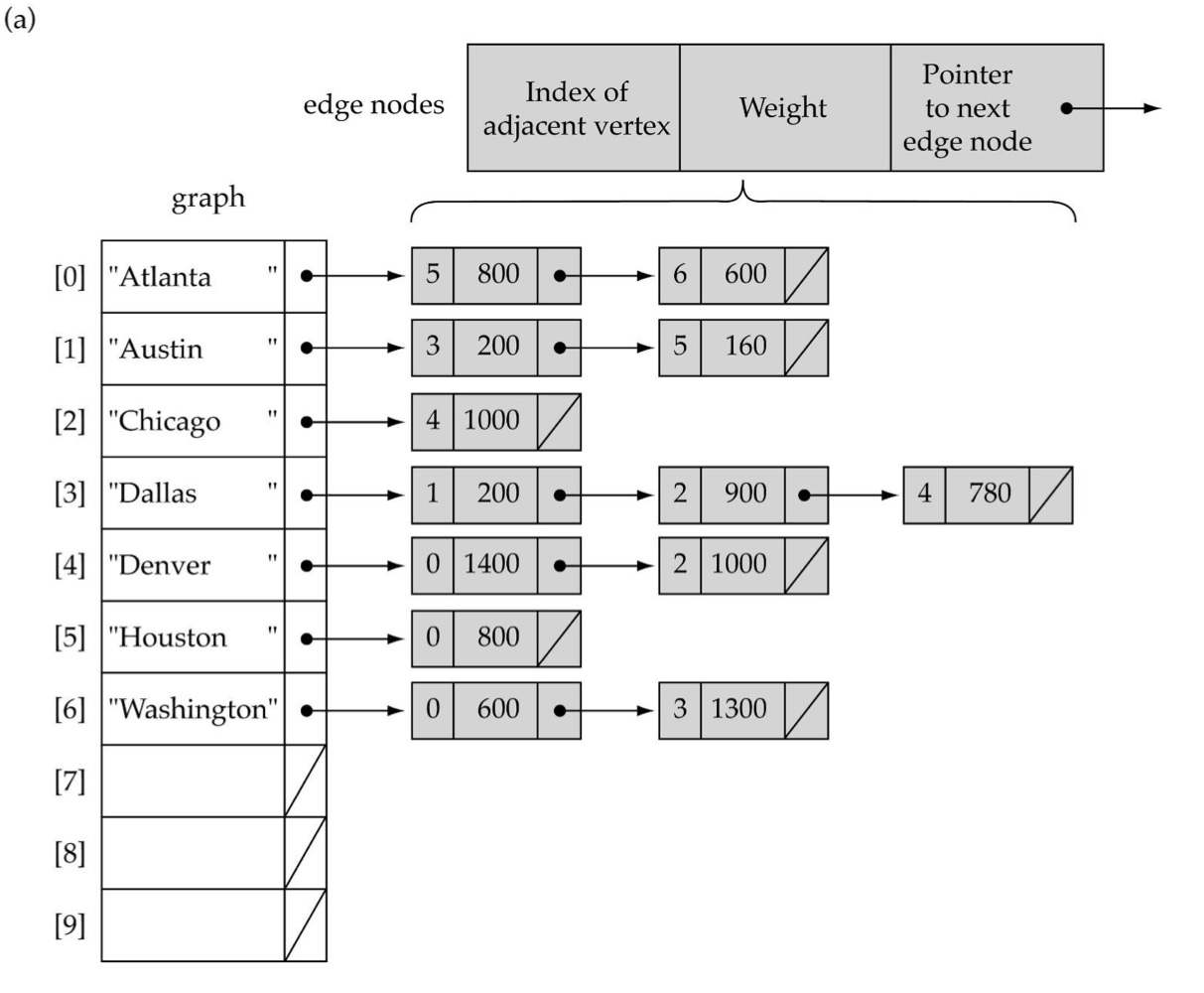
- Sorted인 경우 이진 탐색 O(logN), Unsorted인 경우 완전 탐색 O(N)
- edges[0][5]=800: vertices[0]인 Atlanta와 vertices[5]인 Houston 사이를 이어 주는 800이라는 weight를 가진 path 존재
- python 구현
A / \ B---C | A | B | C | ---|---|---|---| A | 0 | 1 | 1 | ---|---|---|---| B | 1 | 0 | 1 | ---|---|---|---| C | 1 | 1 | 0 | ---|---|---|---|INF = 999999999 graph = [ [0, 7, 5], [7, 0, INF], [5, INF, 0] ]from QueType import * from StackType import * NULL_EDGE = 0 def index_is(vertices, vertex): index = 0 while index < len(vertices) and vertex != vertices[index]: index += 1 if not index < len(vertices): return -1 else: return index class GraphType: def __init__(self, maxV=50): self.numVertices = 0 self.maxVertices = maxV self.vertices = [None] * maxV self.edges = [[NULL_EDGE] * maxV for _ in range(maxV)] self.marks = [None] * maxV def add_vertex(self, vertex): self.vertices[self.numVertices] = vertex for index in range(self.numVertices): self.edges[self.numVertices][index] = NULL_EDGE self.edges[index][self.numVertices] = NULL_EDGE self.numVertices += 1 def add_edge(self, fromVertex, toVertex, weight): row = index_is(self.vertices, fromVertex) col = index_is(self.vertices, toVertex) self.edges[row][col] = weight def weight_is(self, fromVertex, toVertex): row = index_is(self.vertices, fromVertex) col = index_is(self.vertices, toVertex) return self.edges[row][col] def get_to_vertices(self, vertex, adjVertices): fromIndex = index_is(self.vertices, vertex) for toIndex in range(self.numVertices): if(self.edges[fromIndex][toIndex] != NULL_EDGE): adjVertices.enqueue(self.vertices[toIndex]) def clear_marks(self): for index in range(self.numVertices): self.marks[index] = False def is_marked(self, vertex): index = index_is(self.vertices, vertex) return self.marks[index] def mark_vertex(self, vertex): index = index_is(self.vertices, vertex) self.marks[index] = True def delete_edge(self, fromVertex, toVertex): row = index_is(self.vertices, fromVertex) col = index_is(self.vertices, toVertex) self.edges[row][col] = NULL_EDGE - C++ 구현
template<class VertexType> class GraphType { public: GraphType(); GraphType(int maxV); ~GraphType(); void AddVertex(VertexType vertex); void AddEdge(VertexType fromVertex, VertexType toVertex, int weight); int WeightIs(VertexType fromVertex, VertexType toVertex); void ClearMarks(); bool IsMarked(VertexType vertex); void MarkVertex(VertexType vertex); void GetToVertices(VertexType vertex, QueType<VertexType>& adjVertices); private: int numVertices; int maxVertices; VertexType* vertices; int edges[50][50]; bool* marks; };// Constructor vertices라는 vertex 저장하는 1차원 array 생성 template<class VertexType> GraphType<VertexType>::GraphType() { numVertices = 0; maxVertices = 50; vertices = new VertexType[50]; marks = new bool[50]; } // Destructor for문 돌면서 vertex에 해당하는 edge들도 삭제 template<class VertexType> GraphType<VertexType>::~GraphType() { delete[] vertices; for (int i - 0; i < maxVertices; i++) delete[] edges[i]; delete[] marks; } // AddVertex vertex array에 새로운 vertex를 넣어 주기 // 새로운 vertex와 연결된 edge는 모두 null로 초기화 // numVertices 하나 증가 template<class VertexType> void GraphType<VertexType>::AddVertex(VertexType vertex) { vertices[numVertices] = vertex; for (int index = 0; index < numVertices; index++) { edges[numVertices][index] = NULL_EDGE; edges[index][numVertices] = NULL_EDGE; } numVertices++; } // AddEdges Edges array에 새로운 edge를 넣어 주기 // IndexIs vertex의 index 정볼ㄹ 저장하는 1차원 배열 vertices와 찾고자 하는 vertex 정보를 입력하면 해당 vertex의 index를 반환해 주는 함수 // row에는 edge가 뻗어나가는 vertex index 저장 // col에는 edge가 들어오는 vertex index 저장 // adjacent matrix에서 row, col 위치에 해당하는 곳에 edge 삽입 template<class VertexType> int IndexIs(VertexType* vertices, VertexType vertex) { int index = 0; while (!(vertex == vertices[index])) index++; return index; } template<class VertexType> void GraphType<VertexType>::AddEdge(VertexType fromVertex, VertexType toVertex, int weight) { int row; int col; row = IndexIs(vertices, fromVertex); col = IndexIs(vertices, toVertex); edges[row][col] = weight; } // WeightIs fromVertex에서 toVertex로 가는 연결에 있는 가중치 반환하는 함수 //IndexIs vertex의 index 정보를 저장하는 1차원 배열 vertices와 찾고자 하는 vertex 정보를 입력하면 해당 vertex의 index를 반환해 주는 함수 // row에는 edge가 뻗어나가는 vertex index 저장 // col에는 edge가 들어오는 vertex index 저장 // adjacenct matrix에서 row, col 위치에 해당하는 곳의 edge 반환 template<class VertexType> int GraphType<VertexType>::WeightIs (VertexType fromVertex, VertexType toVertex) { int row; int col; row = IndexIs(vertices, fromVertex); col = IndexIs(vertices, toVertex); return edges[row][col]; } // travel 시에 방문했던 기록을 남기는 marks array 초기화 template<class VertexType> void GraphType<VertexType>::ClearMarks() { for (int i = 0; i < numVertices; i++) marks[i] = false; } // 해당 vertex가 방문한 기록이 있는지 물어보는 메소드 template<class VertexType> bool GraphType<VertexType>::IsMarked(VertexType vertex) { index = IndexIs(vertices, vertex); return (marks[index] == true); } // 해당 vertex를 방문했다고 기록하는 메소드 template<class VertexType> void GraphType<VertexType>::MarkVertex(VertexType vertex) { index = IndexIs(vertices, vertex); marks[index] = true; } // vertex에서 뻗어나간 edge랑 연결된 vertex를 adjVertices에 Enqueue하는 메소드 template<class VertexType> void GraphType<VertexType>::GetToVertices(VertexType vertex, QueType<VertexType>& adjVertices) { int fromIndex; int toIndex; fromIndex = IndexIs(vertices, vertex); for (toIndex = 0; toIndex < numVertices; toIndex++) if (edges[fromIndex][toIndex] != NULL_EDGE) adjVertices.Enqueue(vertices[toIndex]);
Implementation: Adjacency List
- 리스트로 그래프의 연결 관계를 표현하는 방식
- undirected graph, directed graph 모두 적용 가능
- Vertices: Vertex에 해당하는 index를 알려 주는 1차원 배열
- Vertex list: Vertex 마다 edge로 연결된 다른 노드들을 Linked list로 표현
- 해당 노드에서 뻗어나가는 edge만
- adjacent node의 연결
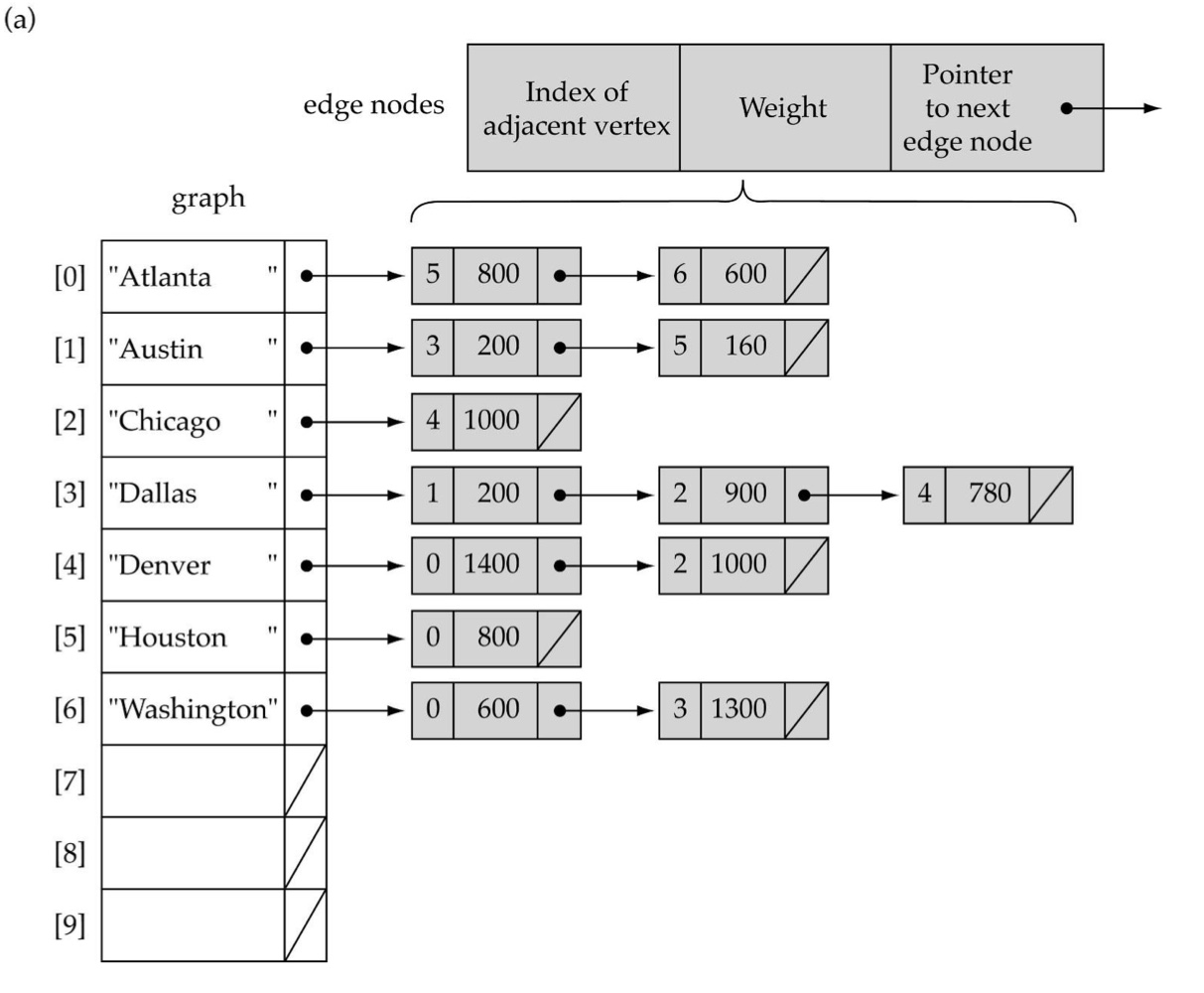
- edges[0][5]=800: vertices[0]인 Atlanta에서 vertices[5]인 Houston까지 가는 데 800이라는 weight를 가진 path 존재
- python 구현
A / \ B---C A -> [B, C] B -> [A, C] C -> [A, B]graph = [[] for _ in range(3)] graph[0].append((1, 7)) graph[0].append((2, 5)) graph[1].append((0, 7)) graph[2].append((0, 5))
Matrix VS List
- matrix
- graph의 크기가 작은 경우에는 유용
- 그래프의 크기가 매우 크면 연결이 없는 부분에 대한 matrix의 메모리 낭비가 발생할 수 있음
- list
- 인접한 노드를 찾기 위해서는 각 노드의 인접 리스트를 순회해야 하기에 search 과정이 오래 걸릴 수 있음
- 노드와 노드 사이 연결 여부를 확인할 때에도 리스트를 순회해야 해서 시간이 소요됨
