Segment Tree

세그먼트 트리의 필요성

문제

• 크기가 N인 정수 배열 A가 있고 여기서 아래와 같은 연산을 M번 수행한다고 가정
  1. 구간 l~r까지의 A[l] + A[l + 1] + … + A[r - 1] + A[r] 구하기
  2. i번째 수를 v로 바꾸기
• 1번 연산은 아래와 같은 코드로 수행 가능

  int ans = 0;
  for (int i=l; i<=r; i++) {
      ans += a[i];
  }

  • 시간 복잡도는 O(N)
• 2번 연산의 시간 복잡도는 O(1)
• 이 과정을 총 M번 하니 전체 시간복잡도는 O(NM)

누적합

• 누적합을 사용하면 1번 연산의 시간복잡도를 O(1)로 구할 수 있음
• 하지만 2번 연산으로 수가 변경될 때마다 누적합을 다시 구해야 해서 2번 연산의 시간 복잡도가 O(N)
• 즉 총 시간복잡도는 O(NM)

세그먼트 트리

세그먼트 트리

• 세그먼트 트리를 사용하면 위에서 말한 연산을 O(logN)에 수행 가능
• 세그먼트 트리에서 노드의 의미
  • 리프 노드: 배열의 수 그 자체
  • 리프 노드가 아닌 노드: 왼쪽 자식과 오른쪽 자식의 합을 저장
• 어떤 노드의 번호가 x일 때 왼쪽 자식은 2x, 오른쪽 자식은 2x + 1
• n = 10인 경우 세그먼트 트리

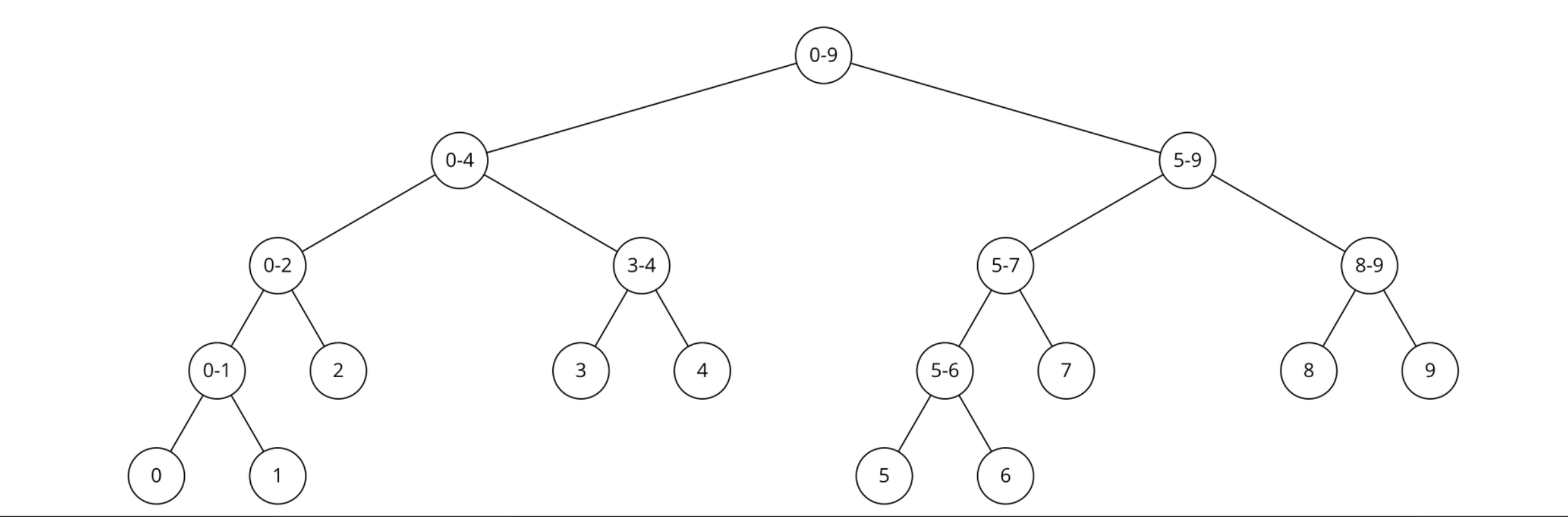
만들기

• 리프 노드를 제외한 다른 모든 노드는 항상 2개의 자식을 가짐
• 따라서 세그먼트 트리는 Full Binary Tree의 형태
• 만약 N이 2의 제곱꼴인 경우는 Perfect Binary Tree
• 리프 노드가 N개인 Full Binary Tree에는 리프 노드가 아닌 노드가 N - 1개 존재
  • 따라서 필요한 모든 노드의 수는 2N - 1
• 높이 h = logN

// a: 배열 A
// tree: 세그먼트 트리
// node: 노드 번호
// node에 저장되어 있는 합의 범위가 start - end
void init(long[] a, long[] tree, int node, int start, int end) {
    if (start == end) {
        tree[node] = a[start];
    } else {
        init(a, tree, node * 2, start, (start + end) / 2);
        init(a, tree, node * 2 + 1, (start + end) / 2 + 1, end);
        tree[node] = tree[node * 2] + tree[node * 2 + 1];
    }
}

• start == end 인 경우는 리프 노드인 경우 → 배열의 수 자체를 저장
• 리프 노드가 아닌 경우에는 자식 노드들의 합을 저장
• 재귀 함수를 통해 더해야 할 각각의 자식들의 값을 먼저 구함

구간의 합 구하기

• node에 저장된 구간이 [start, end] 이고, 합을 구해야 하는 구간이 [left, right]라면 다음과 같이 4가지 경우

1. [left, right]와 [start, end]가 겹치지 않는 경우
   • 탐색을 이어나갈 필요가 없어서 0 리턴하고 종료
2. [left, right]가 [start, end]를 완전히 포함하는 경우
   • 탐색을 이어나갈 필요가 없으니 루트를 리턴하고 종료
3. [start, end]가 [left, right]를 완전히 포함하는 경우
   • 왼쪽 자식과 오른쪽 자식을 루트로 하는 트리에서 다시 탐색 시작
4. [left, right]와 [start, end]가 겹쳐져 있는 경우 (1, 2, 3 제외한 나머지 경우)
   • 왼쪽 자식과 오른쪽 자식을 루트로 하는 트리에서 다시 탐색 시작

• 합을 구하는 소스

  long query(long[] tree, int node, int start, int end, int left, int right) {
      if (left > end || right < start) {
          return 0;
      }
      if (left <= start && end <= right) {
          return tree[node];
      }
      long lsum = query(tree, node * 2, start, (start + end) / 2, left, right);
      long rsum = query(tree, node * 2 + 1, (start + end) / 2 + 1, end, left, right);
      return lsum + rsum;
  }

• n = 10, left = 3, right = 9인 경우

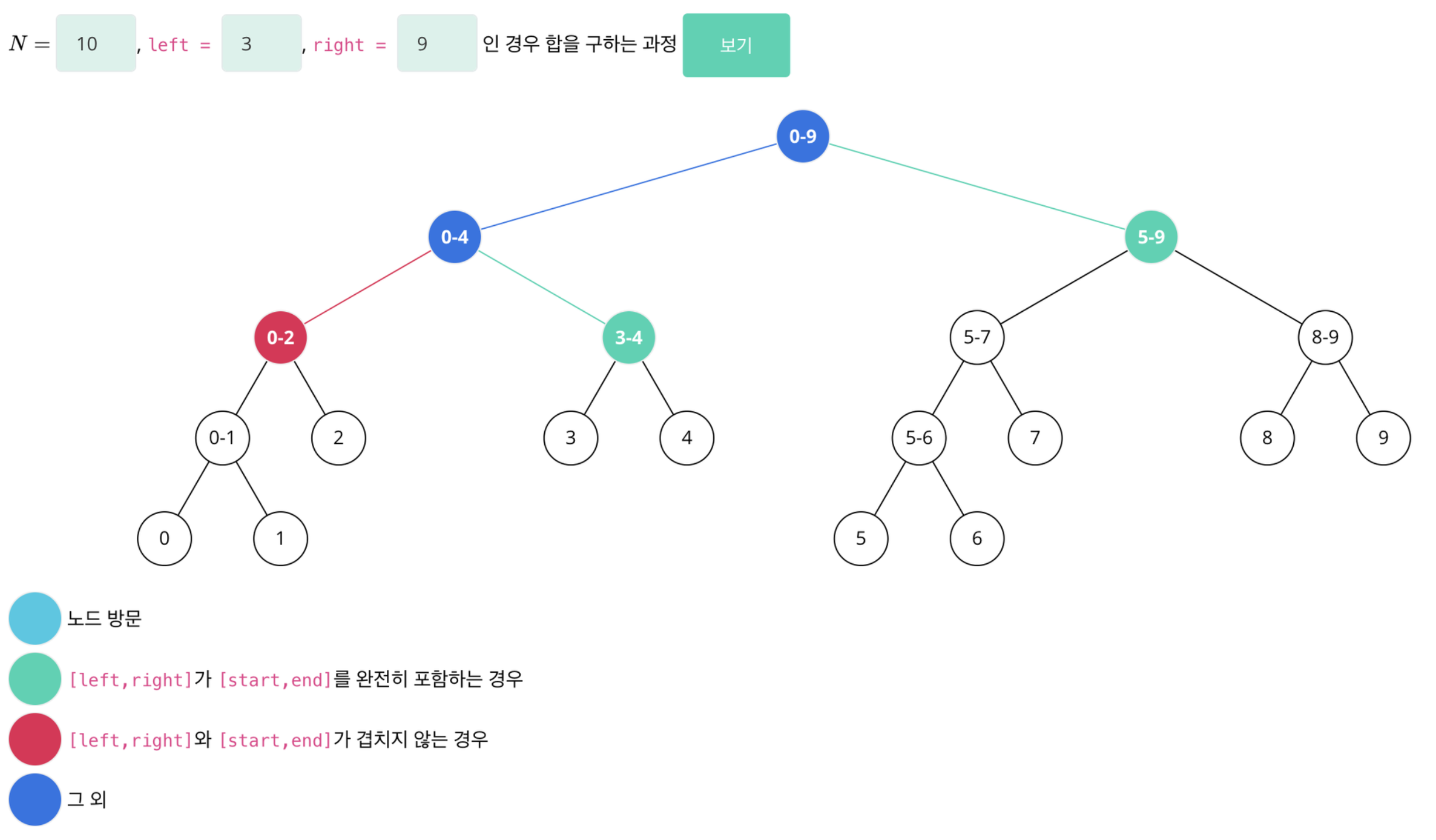
시간 복잡도

• 트리의 각 노드에서 방문하게 되는 노드의 개수는 최대 4개
• 트리의 높이 H
• 따라서 시간복잡도는 logN = H

수 변경하기

• index번째 수를 val로 변경하는 경우, index번째를 포함하는 노드에 들어있는 합만 변경
• 수 변경의 경우
  1. [start, end]에 index가 포함되는 경우
     • 재귀 호출
  2. [start, end]에 index가 포함되지 않는 경우
     • 재귀 호출 중단
• index번째 수를 val로 변경하는 코드

  void update_tree(vector<long long> &tree, int node, int start, int end, int index, long long diff) {
      if (index < start || index > end) return;
      tree[node] = tree[node] + diff;
      if (start != end) {
          update_tree(tree,node*2, start, (start+end)/2, index, diff);
          update_tree(tree,node*2+1, (start+end)/2+1, end, index, diff);
      }
  }
  void update(vector<long long> &a, vector<long long> &tree, int n, int index, long long val) {
      long long diff = val - a[index];
      a[index] = val;
      update_tree(tree, 1, 0, n-1, index, diff);
  }

• N = 10, index = 3인 경우 변경하는 과정
  

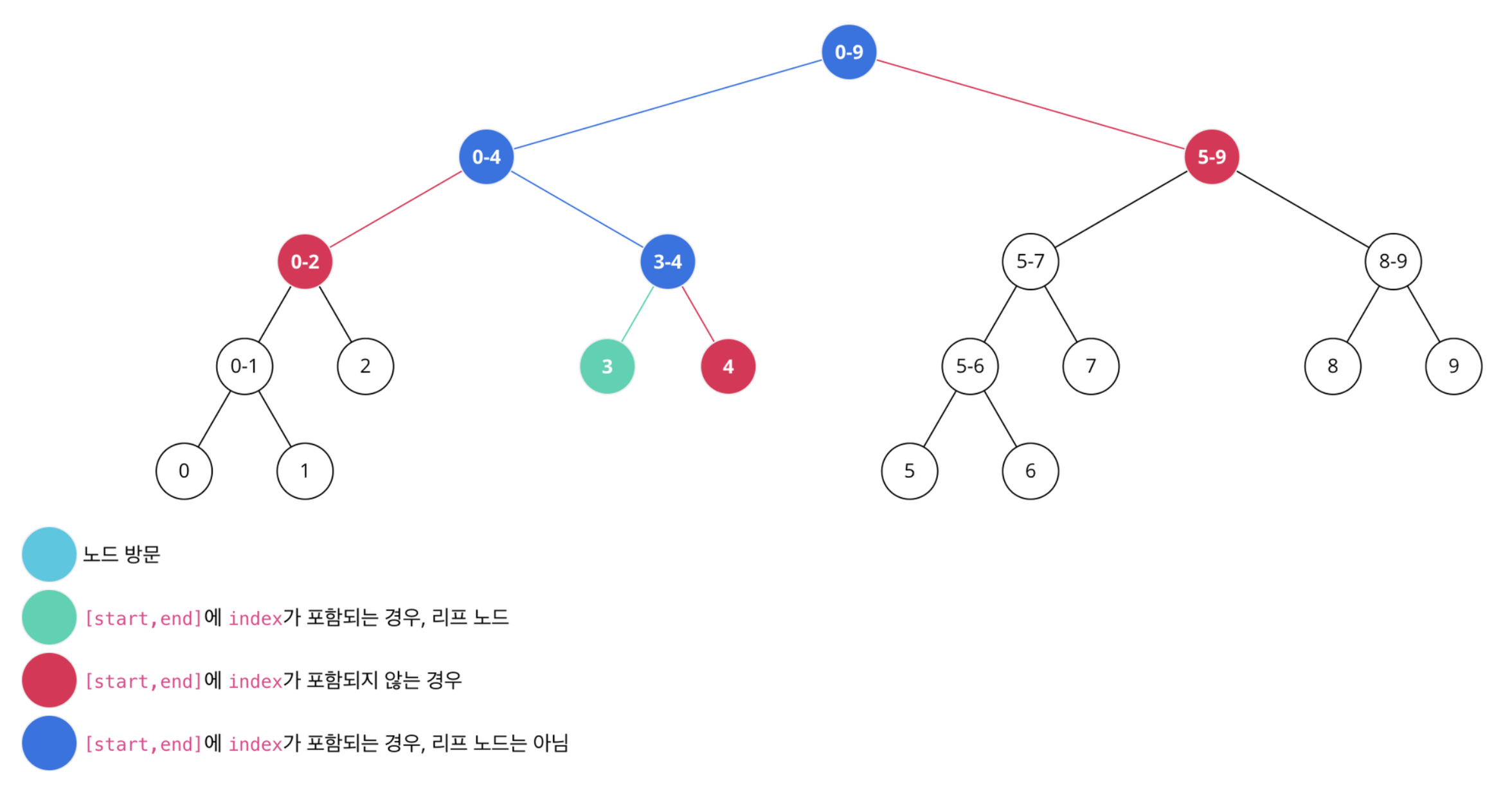
수 변경하기 2

• 리프 노드를 찾을 때까지 계속 재귀 호출을 이어나감
• 리프 노드를 찾으면 그 노드의 합을 변경
• 이후 리턴될 때마다 각 노드의 합을 자식에 저장된 합을 이용해 다시 구함

void update(long[] a, long[] tree, int node, int start, int end, int index, long val) {
    if (index < start || index > end) {
        return;
    }
    if (start == end) {
        a[index] = val;
        tree[node] = val;
        return;
    }
    update(a, tree,node*2, start, (start+end)/2, index, val);
    update(a, tree,node*2+1, (start+end)/2+1, end, index, val);
    tree[node] = tree[node*2] + tree[node*2+1];
}