스터디 - 고정소수점, 부동소수점

고정소수점

10진법에서의 소수점 체계를 이진법에 그대로 적용시킨 것과 같다고 볼 수 있다.

3.25라는 실수를 예로 들어보면
앞의 정수부 3과 뒤의 소수부 0.25로 나누어 볼 수 있다.

전자는 4비트 부호체계로 보면 0011이 될 것이다.
후자는 2의 -2승과 같으므로 소수점 둘째짜리가 1이 되어 소수부는 01로 표현될 수 있다.

만약 1바이트체계라면 8개비트에 정수부와 소수부가 들어가게 되므로 결과적으로
0011.0100
이런 형태가 된다.

이 방식의 단점은 표현가능한 수의 범위가 적고 정밀도가 떨어진다는 것이다.

일단 소수점을 어디에 찍을 것인가?
소수부에 6비트를 할당하면 나머지 정수는 나머지 2비트로 밖에 표현할 수 없다.
만약 정수부에 비트를 할당하면 소수부에 할당된 비트가 줄어들어 정밀도가 떨어진다.

예

정수부에 5비트 소수부에 3비트를 할당했다고 치자.
그럼 소수는 2^(-3), 즉 0.125씩 증감하게 된다.
한 바이트인데도 이렇게 정밀도가 떨어지면 도저히 써먹을 게 못된다.

부동소수점

소수를 이진법으로 표현하는 방법은 고정소수점만 있는 것이 아니다.
국제표준기구에서 표준으로 정한 IEEE 754는 대표적인 부동소수점 체계로 현대의 컴퓨터들의 실수체계는 이를 따르고 있다.

비트할당

부동소수점이 비트를 어떻게 할당하는 지부터 알아보자.

위의 네모칸은 비트들을 의미하고 네모칸의 크기가 클 수록 할당된 비트가 크다는 의미이다.

• S는 부호비트로 1비트를 할당 받는다. 숫자에 몇 바이트가 할당되어도 부호는 1비트다.
• Exponent는 2의 Bias와 함께 2의 몇 승이 될 지 결정한다.
• Fraction은 몇 배수가 될 지 결정한다.
• Bias는 할당 비트 수에 따라 다르다.

-0.75를 부동소수점으로 바꿔보자.
위의 수식에 따라

-0.75 = (-1)S X (1+Fraction) X 2(Exponent-Bias)

로 표현될 수 있다.

먼저 음수이므로 S = 1이다.

그리고 부호를 뗀 0.75는 이진법으로 표기해야 한다.
정말 고맙게도 0.75는 2^(음수) 들의 합으로 표현이 가능하고 이는 무한소수로 표현되지 않는다는 것이다.

0.75 = 0.5 + 0.25 = 1/2 + 1/4 이므로 소수점 첫째자리와 둘째자리가 1이 된다.
고정소수점으로 본다면 0.11 이다

이 숫자가 (1+Fraction)*2^(Exponent-Bias) 이다. 즉,

0.11 = (1+Fraction) X 2(Exponent-Bias)

이고 우린 Fraction, Exponent, Bias를 구하면 된다. 3개의 미지수를 어떻게 구하냐는 의문이 들 수 있겠으나 각 숫자들은 형태가 정해져 있다.

• Fraction 은 저 숫자 0.11이 1.xxxx...형태로 변환했을 때의 소수부이다.
• Bias는 비트체계에 따라 정해진 상수이다. 32비트에선 127, 64비트에선 1023이다. 지수를 unsigned로 만들어 표현범위를 늘리기 위해 사용한다.
• 실제 2의 지수는 Exponent-Bias이다.

Normalize

0.11을 1.xxxx...형태로 변환하려면 소수점을 뒤로 빼고 그만큼 숫자가 곱해져야한다.

0.11 = 1.1 X 2(-1)
소수점이 한자리 뒤로가면 수는 2배 커진다. 원래 수를 유지하려면 수를 1/2배 해야한다.

(1+Fraction)*2^(Exponent-Bias)의 형태가 보이기 시작했다.

Fraction

1.1 = 1+Fraction이다. 따라서 Fraction은 0.1이다.

Exponent, Bias

2^(-1) = 2^(Exponent-Bias)이다.
-1 = Exponent - Bias가 되므로 Bias-1이 Exponent이다.

• 32비트에서 Bias는 127이고, 따라서 Exponent = 126이다.
• 64비트에서 Bias는 1023이고, 따라서 Exponent = 1022이다.

비트에 할당

이제 구한 수들을 이진수로 변환해서 넣어주기만 하면된다.

• Single Precision(32bit)에선 Fraction이 전체의 23비트를 차지한다.
• Double Precision(64bit)에선 Fraction이 전체의 52비트를 차지한다.

0.1의 Fraction은 소수점 부분이 1 하나밖에 없다. 그 뒤는 모두 0으로 채우면 된다.
(왜 그렇게 하냐고 묻지말자. 이건 약속된 표준이다.)

Fraction = 10000000...0 //전체 23비트, 32bit에서
Fraction = 10000000000 // 전체 52비트, 64비트에서

Exponent들을 이진법으로 바꿔주자

• Single Precision(32bit)에선 Exponent가 전체의 8비트를 차지한다.
• Double Precision(64bit)에선 Exponent가 전체의 11비트를 차지한다.

  Exponent = 01111110 // 32bit
  Exponent = 01111111110 // 64bit

S	Expponent	Fraction

의 위치에 구한 수를 넣어주면 끝이다.

-0.75는
32비트에선 1011111101000....0
64비트에선 1011111111101000....0
(중간 0 생략)

---

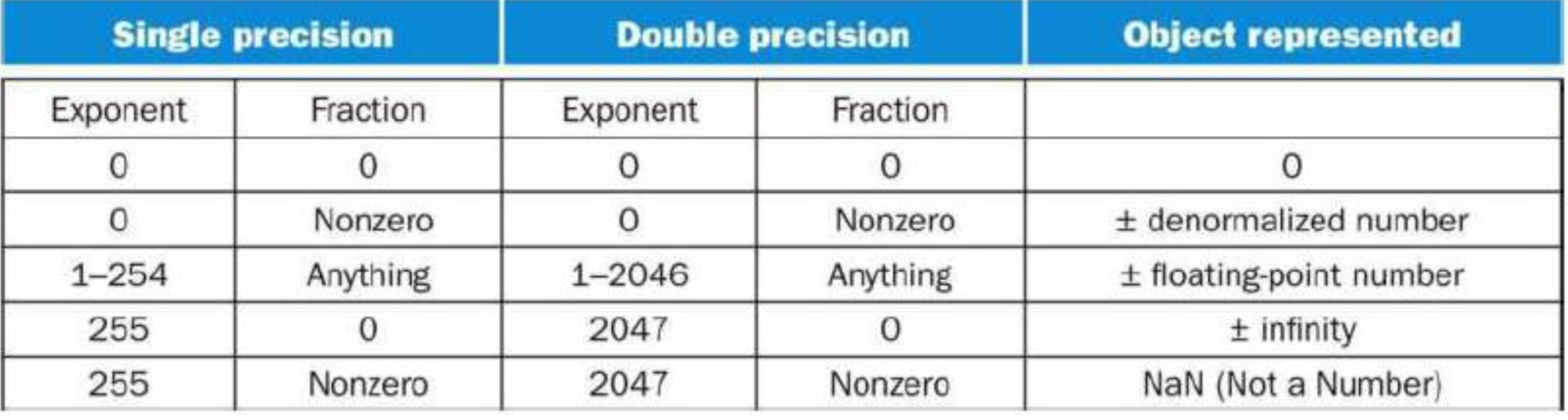
Denormal Numbers

앞에선 Normal Numbers의 변환방법이다.
0그리고 절댓값이 매우 작은 소수를 Denormal Value라고 한다.
정규화(Normalize)를 할 수 없기때문이다.
Exp가 0이면 이 수는 Denormal Value이다.

이 때의 Exponent는 1-Bias로 계산한다.

• Exponent가 0이고 Fraction도 0이면 그 수는 0이다.
• Exponent가 0이고 Fraction이 0이 아니면 매우 작은 수이다.

Special Value

Special Value는 예약되어있는 특수한 수이다.
Exponent가 1111...1이면 Special Value이다.
Infinity 와 Nan을 표현한다.

• Special Value의 Fraction이 0이면 무한대이다.
• Special Value의 Fraction이 0이 아니면 Nan이다.

---

반올림

십진법에서는 자릿수가 5미만이면 내림, 5이상이면 올림을 하는 식으로 반올림한다.

컴퓨터도 이진법을 저장할 때 분명히 소숫점이 허용량을 벗어나는 경우가 생길 것이고 이럴 때에는 반올림을 해야할 것이다.

반올림은 실제 소수부분을 담고 있는 Fraction 부분을 해야할 것이며
Single Precision이든 Double Precision이든 Fraction에게 할당된 비트의 수는 한정돼있다.

1.001011

빨간색 부분에 대해

• 내림하면: 1.001000
• 올림하면: 1.001100

기본교육에는 나오지 않는 어림방법이 있는데 nearest-even 이 있다.
말그대로 가장 가까운 짝수가 되도록 어림하는 것이다. 이진수에선 가장 가까운 수 중 끝자리가 0인 것이다.

다시 빨간색 부분에 대해 nearest-even을 하면
1.001000이다.

소수점 3째자리까지를 반올림할 것이므로 반올림의 후보는
1.001000과 1.010000 이다. 이중 원래의 수에 더 가까운 수는 전자이다.

그럼 1.001000을 반올림하려면 어떻게 해야 할까
소수점 3째자리에서 반올림을 해야한다.
1.010000과 1.000000의 후보가 나왔는데 문제가 생겼다.
두 수와 1.001000 의 거리가 동일하다.

이런 경우엔 ties-to-even을 한다. 끝자리가 0이 되도록 하는 것이다. 이 경우 내림을 선택한 1.000000이 반올림 결과가 된다.

GRS비트에 대한 공부가 소수점의 어림을 이해하는데 도움을 줄 것이다.

---

부동소수의 연산

곱하기

결과의

• S : s1^s2
• M : M1 X M2
• E : E1 + E2

후처리
다시 정규화(1.xxx형태로 맞추고 지수를 조정)하고 반올림한다.

더하기

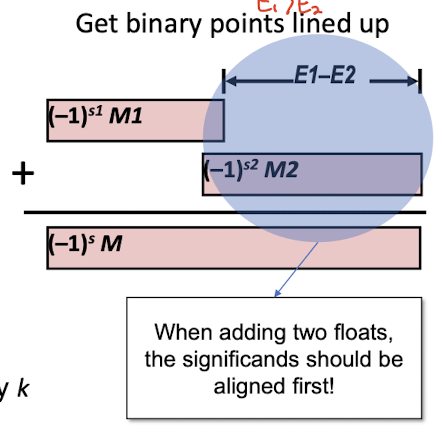
더하기의 경우에는 지수가 같도록 맞춰줘야 한다. E2가 E1보다 작다면 지수를 E1으로 맞추고 연산한다.

마찬가지로 후처리를 한다.

연산결과의 부정확성

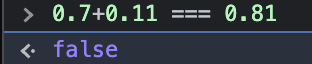
연산과 후처리과정을 이해했으면 이 식이 왜 false인지 알 수 있다.
이해가 되지 않는다면 직접 부동소수점으로 바꾸고 더해보자.

부동소수점 덧셈의 특성

• 덧셈에 폐쇄적이다: 덧셈의 결과 또한 부동소수점이다
• Commutative: A+B == B+A
• Not Associative: 결합법칙이 작용하지 않는다.
  (3.14 + 1e10)-1e10 = 0 // 괄호에서 오버플로우
  3.14 + (1e10-1e10) = 3.14
• 0 is additive identity: A+0 == A-0
• Special Value를 제외하면 additive inverse(더했다 빼면 값 그대로)함
• Special Value를 제외하면 monotonicity: a >= b -> a+c >= b+c 는 참

부동소수점 곱셈의 특성

• 곱셈에 폐쇄적
• Commutative: A X B == B X A
• 결합법칙이 유효하지 않음
• 1 is multiplicative identity
• 분배법칙이 유효하지 않음
• Special Value를 제외하면 monotonicity: a >= b -> aXc >= bXc 는 참