배낭훔치기 알고리즘

S = {item1,item2 ... }
Wi = item의 무게
Pi = item의 가치
W = 배낭에 넣을 수 있는 최대 무게

무게가 넘지 않으면서 가치가 최대가 되도록 A를 결정

Brute force 알고리즘

• n개의 물건에 대해서 모든 부분 집합을 다 고려함
• 크기가 n인 집합의 부분집합 수는 2^n개...

Greedy Approach

0-1 The Knapsack Problem 1

• 가장 비싼 물건부터 우선적으로 채운다
• 최적 알고리즘은 아니다!

=> 값어치를 기준으로 했을 때 최적이 아님..

0-1 The Knapsack Problem 2

• 물건이 쪼갤 수 없는 거라고 가정할때
• 무게당 값어치를 만들어서 이거를 기준으로
• 그래도 최적 알고리즘이 아님!

The Fractional Knapsack Problem

• 훔칠수있는 아이템을 가루라고 생각
• 무게당 값어치를 기준으로 하면 풀려=> 반만 훔쳐가는 행위까지 하면 최적 알고리즘!

0-1알고리즘은 그리디 알고리즘으로는 안풀려!

=> 다이나믹 알고리즘으로 풀어야해

Dynamic Programming

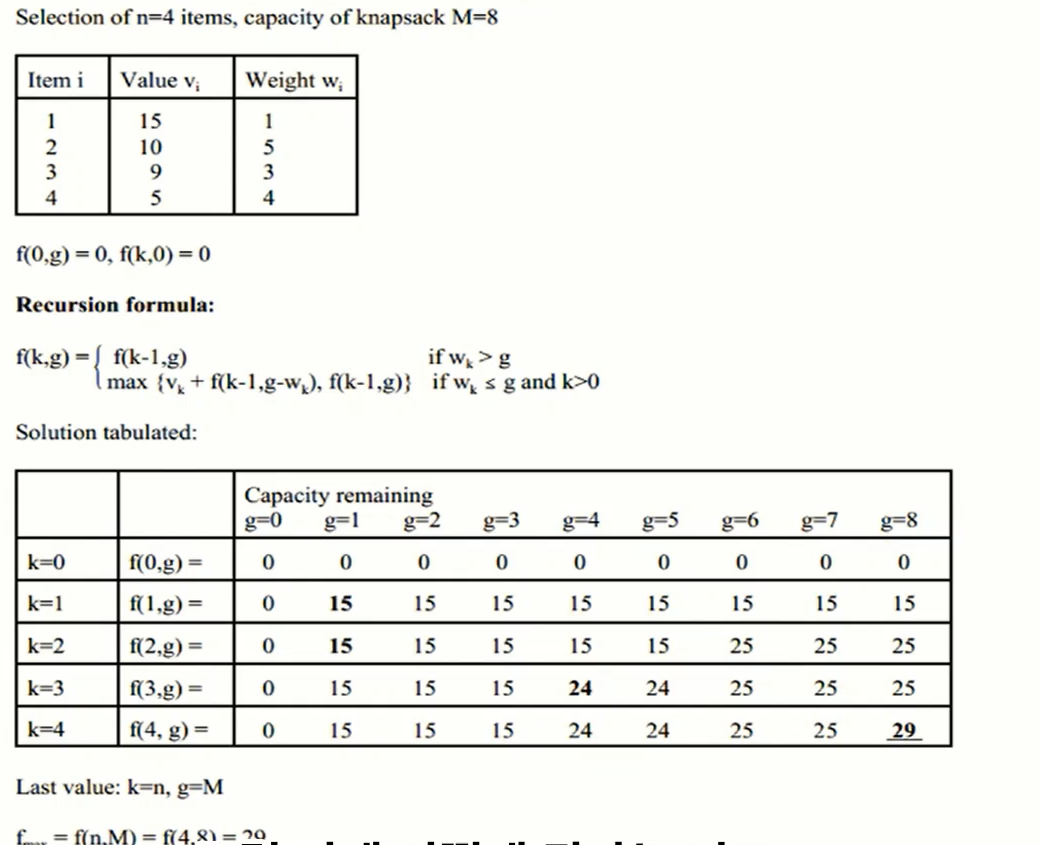- 아이템이 4개가 있다고 가정

새로 아이템을 추가한다고 생각해서 그 전 답을 이용하자

점화식

• Wi가 배낭 용량을 넘지는 않을때 가방에 넣는걸 시도 할 수 있어

• max(첫번째가 실패한 상황, 두번째가 성공한 상황)

• 배낭 용량이 w니까 나머지 여유는 [w-wi]. 최고로 잘 채워졌을때는 [i-1].

• pi랑 wi는 입력으로 주어짐

성능분석

• 한칸을 채우는걸 B.O 으로 하면 O(nW)
  n은 아이템 개수, W는 배낭 용량

근데 둘은 아무 상관관계가 없자나..
최악의 경우를 따지면 성능이 brute force만 못해

=> 다 계산 안하고 필요한 것만 계산해서 성능을 높이자!!

원래대로 했으면 3 * 30 해야하는데
필요한것만 계산하면 7 번만 하면됨

근데 필요한건만 어떻게 알아내지?

=> Top-Down 으로 원하는거만 접근 -> D.C

• D.C의 단점을 보완하기 위해 한번 계산을 해놓은거는 어딘가에다가 저장을 해놔 = Dynamic Programming memorization 기법(DP인데 Top-down)

• 답이 저장소에 있으면 참조하고, 호출 X하자

DP memorization

최악의 경우는 O(2^n). Brute force는 항상 (2^n)인데 DP는 최악의 경우가 이거임. 더 낫다

최악의 경우는 필요한거만 계산하는데 겹치는게 한번도 발생을 안할때 => (2^n)-1

최고의 경우는 항상 겹칠때 => n + n-1 + n-2 +...+1 = O(n^2)

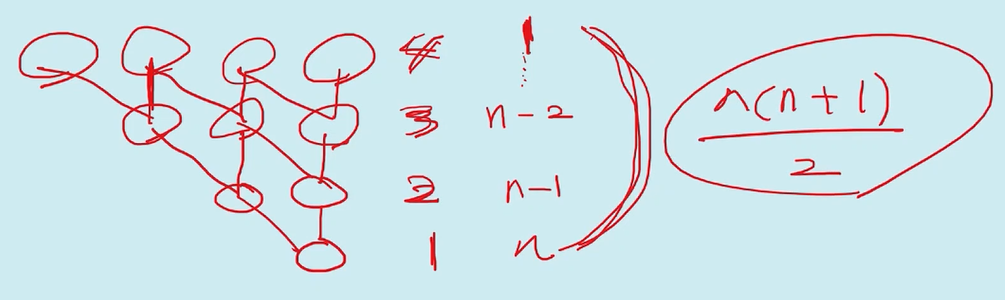
결론

• 아직 지수보다 나은 알고리즘을 발견하지 못함
• 아직 아무도 근데 결론을 못냈음
  => NP문제