문제

어느 날, 정말로 은행을 털어보고 싶다는 생각이 든 시로코는 은행을 털 준비를 하기 시작했다. 우선, 은행 터는 것을 함께 할 팀을 만들 것인데, 경쟁을 뚫고 마지막까지 살아남은
$n$명 중에서 최종적으로
$k$명을 팀원으로 선발할 계획이다. 지원자들은 각각 힘과 스피드 수치
$a$,
$b$가 주어지는데, 쟁쟁한 경쟁을 뚫고 살아남은 자들답게
$a+b$가 모두 동일하다.

$i$번째 팀원으로 선발한 사람의 능력치가 각각
$a_{i}$,
$b_{i}$라 할 때, 그 팀의 종합 능력치는
$(\sum\limits_{i=1}^{k} a_{i})\times(\sum\limits_{i=1}^{k} b_{i})$이다. 팀의 능력치를 최대화하게 지원자들을 선발하려 할 때 그때 그 팀의 능력치를 출력하라.

입력

첫 번째 줄에 사람의 수
$n$와 뽑을 인원
$k$, 그리고 힘과 스피드 수치의 합
$x$가 공백으로 구분되어 주어진다.

그 다음줄부터
$n$개의 줄에는 각 사람들이 지닌 힘과 스피드 능력치
$a$
$b$가 주어진다.

출력

팀의 능력치를 최대화하게 인원을 선발할 때, 그 팀의 능력치를 출력하라.

제한

$1 \leq n \leq 80$ 

$1 \leq k \leq n$ 

$1 \leq x \leq 200$ 

$0 \leq a, b$ 

풀이

분석

수학적인 규칙 찾기

종합 능력치가 팀원의 힘과 스피드의 합을 곱하는 것이므로 먼저 최대치가 될 수 있는 수치에 대해 생각해야 한다.

먼저 팀원 하나에 대한 최댓값을 생각해보았다.
대략적으로 추정했을 때, a=b 즉 n/2 제곱이 되어야 최대치가 되어야 된다고 생각했다.

증명해보자.
a+b = n이므로, b=n-a
ab를 f(x)라는 함수로 정의 시
$f(x) = ab = a(n-a) = an-a^2$
이 함수의 최댓값이 ab의 최댓값이 된다. 최고차항이 이차함수이므로 기울기가 0이 될 때 최댓값이 나온다. 미분 해보자.
$f'(x) = n-2a$
$2a = n$, 즉 $a = b = n/2$일 때 f(x)는 최댓값이 된다.

팀원이 여러명일 때에 대해 생각해보자.
사실 팀원이 여러명일 때도 유사하다.
문제 조건에서 a+b가 모두 동일하게 주어졌으므로, k명일 시 총합은 $(a+b)*k$이다.
이때도 최댓값은 $\sum\limits_{i=1}^{k} a_{i} = \sum\limits_{i=1}^{k} b_{i} =nk/2$이다.

그런데 문제에서는 nk/2가 되는 합이 나오지 않을 수 있다는 것이다.
이럴 때는 $\sum\limits_{i=1}^{k} a_{i}$와 $\sum\limits_{i=1}^{k} b_{i}$의 차(절댓값)가 가장 작은 것이 최댓값이 된다.

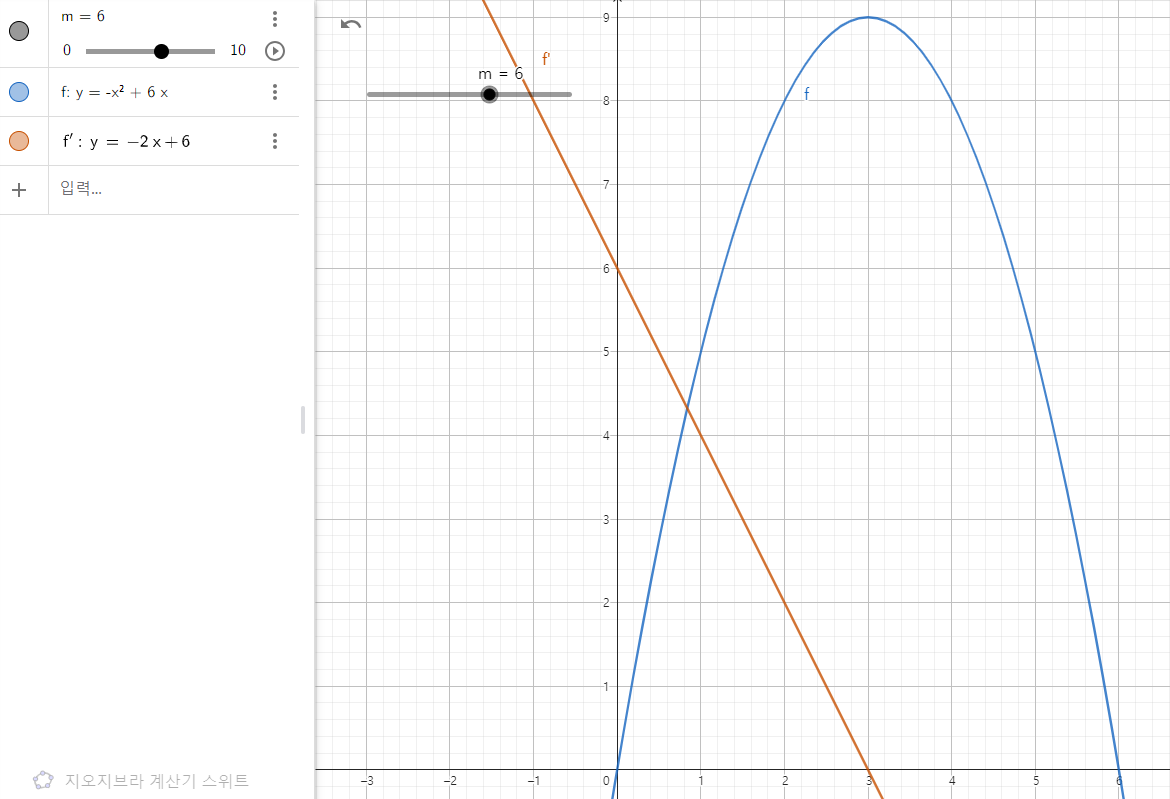
그림판은 너무 처참해서 지오지브라를 가져왔다
기울기가 0에 가까울 수록 종합능력치 함수 f(x)의 값이 높아지기 때문에 최댓값이 되는 것이다
이제 수학적인 규칙은 다 본 것 같으니 어떻게 풀지 생각해보자...

알고리즘

n명 중에 k명의 조합으로 최적해(최댓값)을 찾아내는 것이다.
물론 나이브하게 구하려하면 O(n!)문제가 된다.
1명일 경우 최적해, 2명일 경우 최적해... 마지막으로 k명일 경우 최적해를 구하는 축소정복 및 바텀업 방식(탑다운도 될거다. 아마도..!)으로 해결한다면 $T(n) = nk$로 풀 수 있을 것이다. 최악의 경우 k=n이므로 $O(n^2)$인 문제가 되겠다.
헉! 다이나믹 프로그래밍이다!

a와 b를 입력받고 a-b를 리스트에 저장한다.
최적해를 구할 시, |a-b|가 최솟값이 되는 것이 조건이기 때문에 abs() 함수를 씌워주었다.

import sys
input = sys.stdin.readline

n, k, x = map(int, input().split())

dp = [0] + [float('inf')]*(k)
bag = []

for i in range(n):
    a,b = map(int, input().split())
    bag.append(a-b)

for i in range(n):
    for j in range(1, k+1):
        dp[j] = min(dp[j], abs(dp[j-1]+bag[i]))

print(dp[-1])

sum(a-b)가 최소인 값을 찾는 코드이다.
이때, sum(a-b)를 알면 sum(a)와 sum(b)의 곱을 알 수 있다.

sum(a)를 A, sum(b)를 B라고 할때...
A+B=xk
B=(xk)-A
A-B = 2A-xk
sum(a-b) = A-B = 2A-xk
따라서 A = (sum(a-b)+xk)/2가 된다.
예제를 통해 값이 잘 나오는 지 확인해보았다.

k가 3이고 최적해를 이루는 a,b가 다음과 같을 경우...
3 4
4 3
3 4
sum(a-b) = -1
xk = 21
20/2 = 10
a = 10, xk-a=b=11
홀수에서도 잘나온다! 바로 코드를 작성해보자.

#계산식
A = (n*k+dp[-1])//2
B = n*k-A
print(A*B)

이걸 좀 더 최적화하면 어떻게 될까라는 생각을 해보았다...
dp[-1]을 r이라고 할 시, B = nk-(nk+r)//2
(nk+r)/2가 항상 정수일 때 B = (nk-r)//2 = (nk-r)/2
$AB = (nk^2-r^2)/4$를 넣어도 되지 않을까????
그래서 바로 넣어봤다.

그리고 둘다 틀렸다

이번엔 반례가 어떤 게 있나 싶어 질문게시판을 참고하였다.

반례

4 2 4
0 4
0 4
0 4
0 4

abs()를 사용한 정보를 저장해서 부호가 사라져 코드가 꼬여버린다.
따라서 반복문 부분을 수정해주었다...

for i in range(n):
    for j in range(1, k+1):
        if abs(dp[j]) > abs(dp[j-1]+bag[i]):
            dp[j] = dp[j-1]+bag[i]

하지만 이 경우 같은 사람을 여러번 선택할 수 있다는 문제가 발생한다.
따라서 탑-다운 방식으로 내려가야 문제를 해결할 수 있다...

++++

4 2 4
2 2
0 4
4 0
1 3

다음과 같은 형태의 입력도 15를 반환한다.
이전 답안에서 최적해에 들어가지 않는 인원이, 현재 답안에서 들어갈 수 있기 때문이다.
따라서, 1차원 리스트는 문제 해결에 적합하지 않다고 생각해 n*k 행렬을 만들어 3중 반복문을 돌려주기로 했다.

import sys
input = sys.stdin.readline

n, k, x = map(int, input().split())

dp = [[0] + [float('inf')]*k for _ in range(n)]
bag = []
r = float('inf')

for i in range(n):
    a,b = map(int, input().split())
    bag.append(a-b)

for i in range(n):
    for j in range(k, 0, -1):
        dp[i][1] = bag[i]
        for ii in range(i): # 이전까지의 물건들 조회
            if abs(dp[i][j]) > abs(dp[ii][j-1]+bag[i]):
                dp[i][j] = dp[ii][j-1]+bag[i]
        r = min(r, abs(dp[i][-1]))

A = (x*k+r)//2
B = x*k-A
# print(dp, bag)
# print(A, B)
print(A*B)

응 아니야

import sys
input = sys.stdin.readline
n, k, x = map(int, input().split())
dp = [[0] + [float('inf')]*k for _ in range(n)]
bag = []
r = float('inf')
for i in range(n):
    a,b = map(int, input().split())
    bag.append(a-b)
for i in range(n):
    dp[i][1] = bag[i]
    for ii in range(i):
        for j in range(k, 1, -1):
            if abs(dp[i][j]) > abs(dp[ii][j-1]+bag[i]):
                dp[i][j] = dp[ii][j-1]+bag[i]
    r = min(r, abs(dp[i][-1]))
A = (x*k+r)//2
B = (x*k-r)//2
print(A*B)

추가적인 수정을 거쳐 오버헤드를 최소화했다.
구글링으로 다른 코드도 찾아봤지만 내 코드의 반례를 진짜 못찾겠다.
해설지에서도 k명의 a의 합이 가능한지 여부를 저장하기는 했었다만... a와 b의 차를 이용해서 푸는 것이라 다르지 않을 것인데 오답 처리를 받는다.

짱구를 열심히 굴려보고 구글링을 해본 결과 a의 합을 기준으로 푸는 문제였다.
풀긴 했으나 아직도 내 코드가 안되는 이유를 이해를 못했다. 외않됨???