문제

문제

작년 송년대회에서 여러분의 도움으로 오토에게 양식장을 선물받은 데이브는, 1년 동안 열심히 물고기를 키워 많은 돈을 벌었다. 이 돈으로, 데이브는 양식장을 크게 확장했다! 확장을 마친 양식장은 정사각형 칸이
$N \times M$ 크기의 격자 모양으로 배치된 구조를 가지고 있다.
데이브는 이 양식장에 5가지 종의 물고기를 키우려고 한다. 데이브는 물고기들의 프라이버시를 매우 중요하게 여기기 때문에, 격자 한 칸에는 한 마리의 물고기만을 키운다. 이때, 양식장의 각 칸에서 키울 물고기의 종을 고를 때는 다음 규칙을 지켜야 한다.

같은 종의 물고기는 상하좌우로 인접한 두 칸에서 키울 수 없다. 그렇지 않으면 물고기들이 제멋대로 번식할 수 있기 때문이다.
상하좌우로 4개 칸과 모두 인접한 칸(즉, 양식장의 모서리나 꼭짓점에 인접하지 않은 칸)의 물고기들은, 자신을 제외한 4개 종의 물고기와 모두 인접해야 한다.
데이브는 위 규칙을 따르도록 각 칸에서 키울 물고기를 어떻게 정해야 할지 고민하고 있다. 규칙에 맞는 물고기의 배치를 하나 찾아서 데이브를 도와주자.

입력

첫 번째 줄에 양식장의 크기를 나타내는 두 정수
$N$과
$M$이 공백으로 구분되어 주어진다.

출력

$N$개의 줄에 걸쳐, 각 줄에
$M$개의 정수를 공백으로 구분하여 출력하여라. 이때
$i$번째 줄의
$j$번째 수로는 위에서
$i$번째, 왼쪽에서
$j$번째 칸에서 키울 물고기의 종을 나타내는
$1$ 이상
$5$ 이하의 정수를 출력하여라.

풀이

뇌내 브루트포스를 이용해 풀었다.
규칙 1.
같은 종의 물고기는 상하좌우로 인접한 두 칸에서 키울 수 없다.
규칙 2.
상하좌우로 4개 칸과 모두 인접한 칸(즉, 양식장의 모서리나 꼭짓점에 인접하지 않은 칸)의 물고기들은, 자신을 제외한 4개 종의 물고기와 모두 인접해야 한다.

해당 조건에 따르면, 상하좌우로 4개 칸과 인접한 경우 모든 종의 물고기와 인접해야 한다.
따라서 1 2 3 4 5 와 같은 수열의 순서를 조금만 비틀면 반복 가능한 패턴이 나오지 않을까 하여 직접 만들어 보았다.
운이 좋게도 풀면서 다음과 같은 수열이 나왔다.
하나의 행에서는 1, 4, 3, 2, 5
각 행별 시작 순서(인덱스, 0이 아닌 1부터 시작)는 1, 3, 5, 2, 4
다음과 같이 설정하고 반복할 시 정답 중 하나가 나오게 된다.

하지만 이런식으로 풀게 되면 30점 짜리 기열찐빠 흘러빠진 답안이 아닐 수 없다. 악!!!
머리를 조금 더 써서 패턴의 특징을 알아보자...

같은 종의 물고기는 상하좌우로 인접할 수 없고, 특정 칸에서 인접한 칸에 다른 4개종이 있어야 한다고 했을 때, (i, j) 좌표의 칸에 대해 생각해보자.
이때 (i, j) 좌표의 물고기 종은 N이다.
당연하게도 (i-1, j), (i, j-1), (i+1, j), (i, j+1) 에는 N이 존재할 수 없다.
추가적으로, (i, j)에 N이 존재할 시 (i-1, j), ... 에는 N과 인접했으므로 추가로 N과 인접할 수 없다.
따라서 (i,j)와 인접한 (i-1, j), (i, j-1), (i+1, j), (i, j+1)와 인접한!!! 8칸은 N이 존재할 수 없게 된다.
따라서 좌표(i,j)를 기준으로 다음과 같은 곳에는 N이 존재할 수 없게 된다.

출처 명방 진법캐스터 공격범위ㅎ

각 행마다 N이 존재하면서, 총 종의 개수가 5이므로 행 안에서는 N간의 간격이 4가 되도록 만들면(행 안에 1~5가 모두 존재하게 만들고 싶었다.) 다음과 같은 규칙이 만들어진다.

기준 좌표인 (i, j)를 시작점으로 두고 보기좋게 잘라보았다.

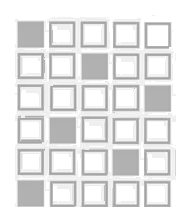
다음과 같이 N이 존재 가능한 좌표의 패턴이 나오게 된다.
행 i와 열 j에 대해,
$j=(i*2)mod5$
라는 관계식이 나온다.

이럴 경우 12345가 반복되는 수열을 슬라이싱해서 그냥 집어 넣어도 정답이 된다.
수열 12345...를 사용한다고 할 때 i와 j에 대한 관계식을 N에 대한 관계식으로 바꿔보자..
$N=((i*3)+j)mod5$

이걸 이용해서 풀면 메모리도 훨씬 적게 사용할 수 있다.

# 수열 구해놓고 풀이
seq = [1, 4, 3, 2, 5]
seq_idx = [1, 3, 5, 2, 4]

N, M = map(int, input().split())

res = []

res = [[seq[(j+seq_idx[i%5]-1)%5] for j in range(M)] for i in range(N)]

for row in res:
    print(*row)

# 단순풀이
N, M = map(int, input().split())

for i in range(N):
    for j in range(M):
        print(((i*3)%5+j%5)%5+1, end=' ')
    print()

풀이 비교.
모듈러 연산이 리소스를 많이 먹어서인지 시간은 단순 풀이가 더 오래걸렸다.

모듈러 연산이 문제였던건지 다른 사람이 이미 풀어본 걸 참고해서... 12345가 반복되는 문자열을 만들어놓고 슬라이싱해봤다. (행에 대해서만 모듈러 연산, 열에 대한 M번의 모듈러 연산 생략)

N, M = map(int, input().split())
seq = '12345'*(M+1) # 1개 추가해서 간격 만들고 여차저차 끼워맞추기
for i in range(N):
    print(*seq[(i*3)%5:(i*3)%5+M])

이때 확실히 속도 개선이 있었다.

나눗셈 쪽이 리소스를 많이 먹는다는 건 알고 있었는데... 이만큼이나 차이가 날줄은 몰랐다.
문제 풀이를 너무 나이브하게 풀었다. 분석에 더 집중해야 할 것 같다...