BOJ 7579 앱 Python

https://www.acmicpc.net/problem/7579
앱 개발자로서 흥미로웠던 문제

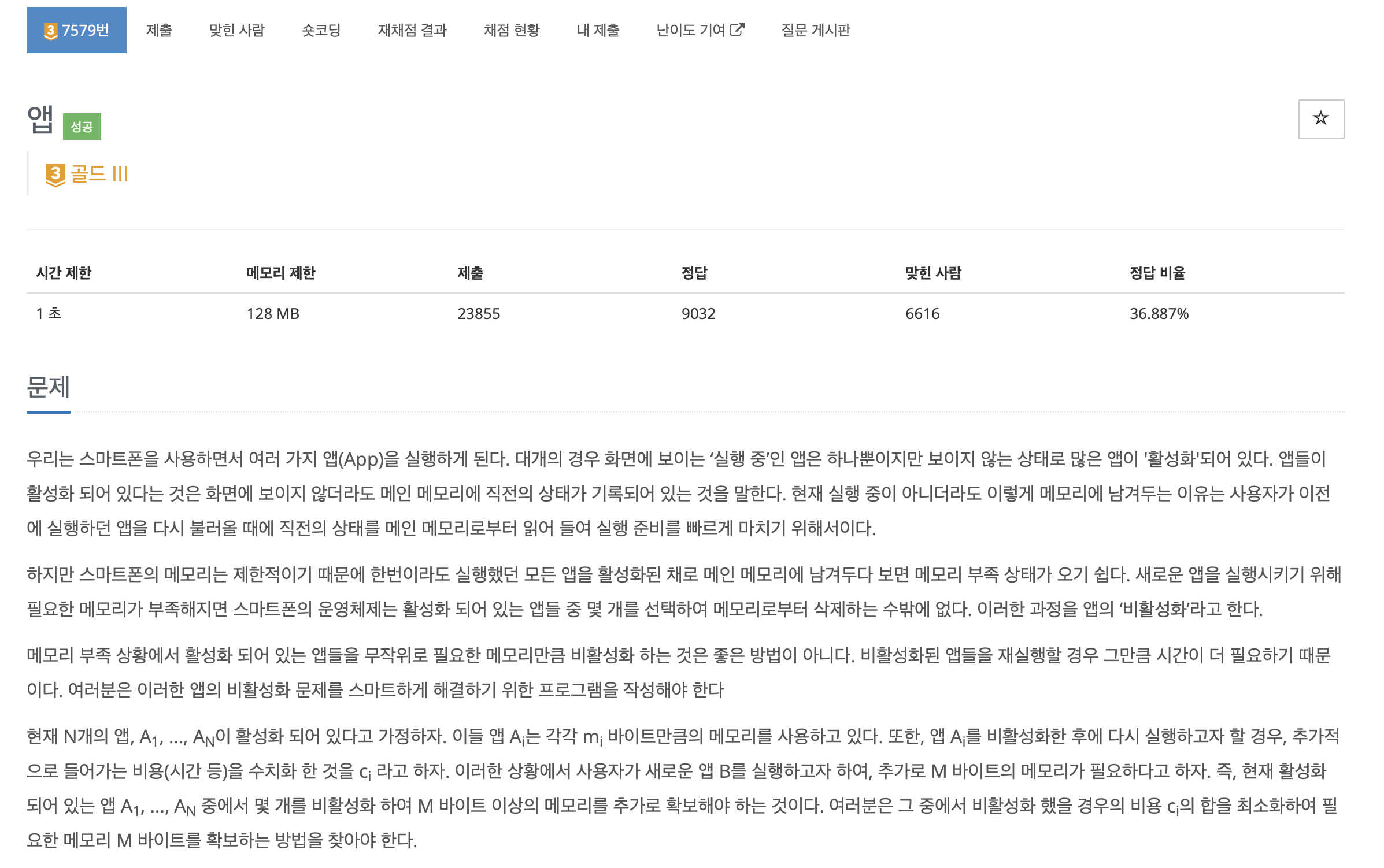
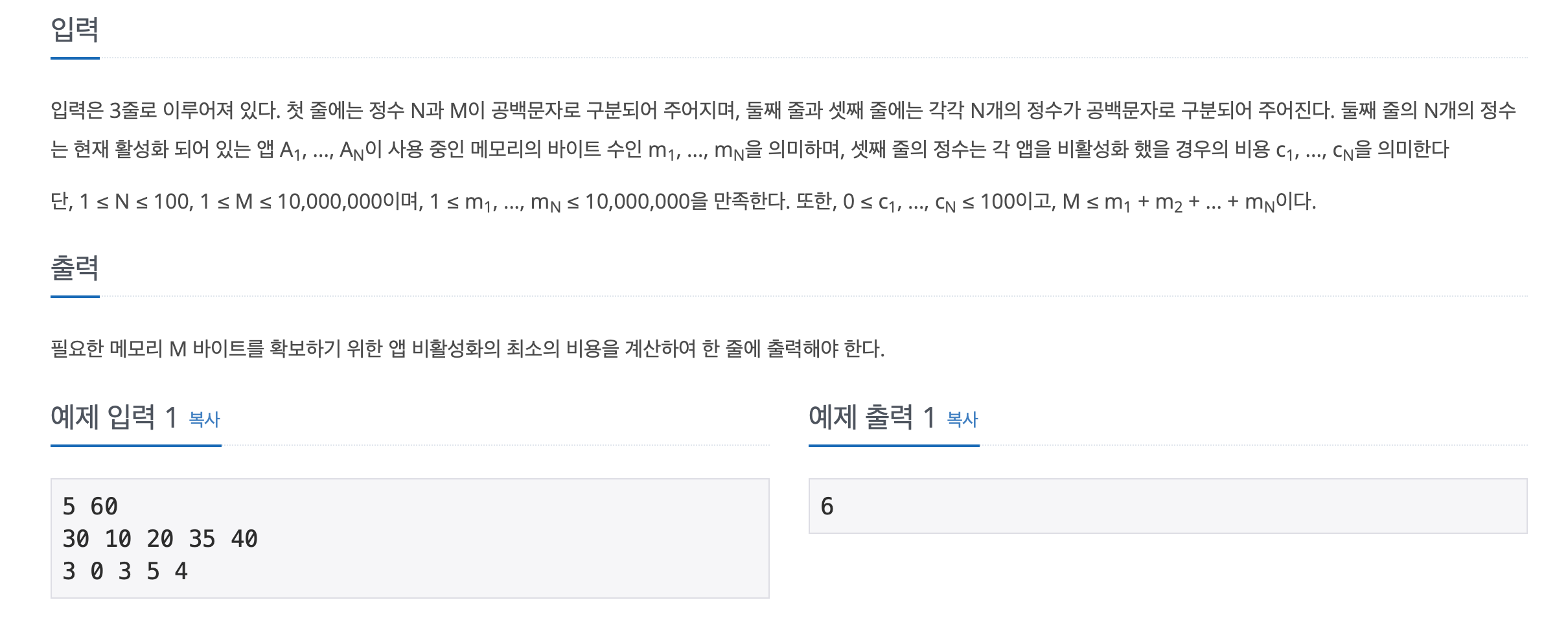
문제에서 요구하는 것)
메모리를 M 만큼 확보하기 위해, 필요한 최소 비용

dp 문제를 많이 풀어 본 사람들이라면 이 문제가 냅색 문제라는 것을 알 수 있을 것이다.

(살짝 어색하다고 느껴지는 이유는, 최대가 아니라 최소 비용을 구하라고 하는점..)

쨌든! 냅색으로 문제를 접근한다면, 무엇을 무게, 무엇을 가치라고 할 것인지 먼저 정의해야한다.

우선,
비용을 최소한으로 사용하여, 최대한 많은 메모리를 확보하는 문제라고 생각해보자.

비용 -> 무게(weight),
메모리 -> 가치(value)

그렇다면 메모리를 확보한 양이 같을때, 비용을 적게 쓸수록 좋다.

문제에서 주어진 예제를 통해 확인해보면

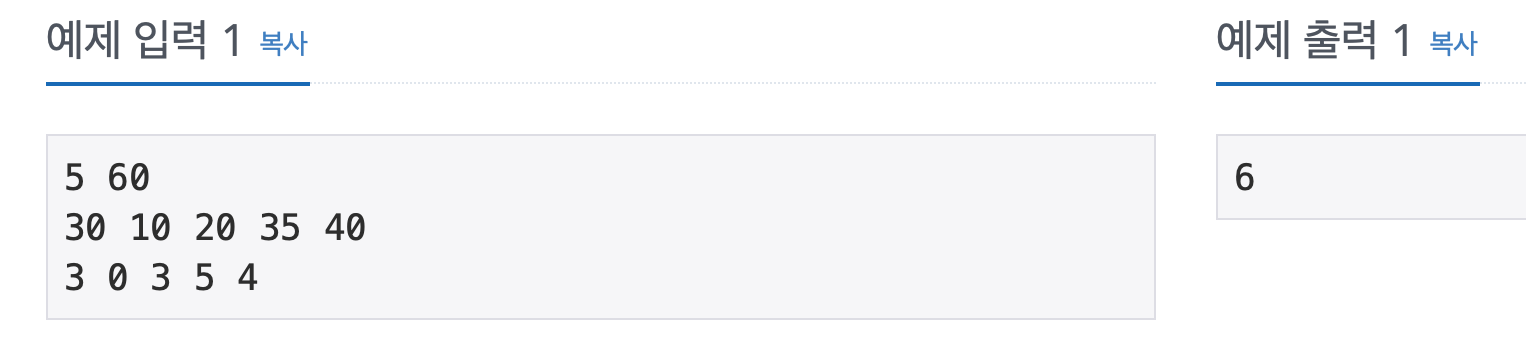
(30, 3), (10, 0), (20, 3) 를 골라 6의 비용으로 총 60의 메모리를 확보한 케이스가
(20, 5), (40, 4) 를 골라 9의 비용으로 총 60의 메모리를 확보한 케이스보다 좋다고 할 수 있다.

그러면 dp 점화식을 세워보도록 하자.

dp[i][j] -> i번째 앱까지 고려하여, j만큼의 메모리를 확보할때 필요한 최소 비용

-> 아쉽게도, 메모리의 범위(1 <= m <=10,000,000)가 너무 크기 때문에,메모리가 dp테이블내에 포함된다면, 모든 케이스를 채우는데에 시간초과, 메모리 초과가 발생한다는 것을 예상할 수 있다.
(앱의 최대 개수 100, 메모리 최대 1000만 -> 100 x 1000만 = 10억)

따라서 불가능 하다...

그렇다면 어떻게 해야할까?

메모리를 가치(value). 비용을 무게(weight)로 생각해보자.

dp[i][j] -> i번째 앱까지 고려하여, j만큼의 비용(무게)을 사용할때 얻을 수 있는 최대 메모리(가치)

우선 '최대' 메모리를 구한다는 점에서, 우리가 항상 풀어왔던 냅색의 문제 정의와 유사해졌다는 것을 확인할 수 있다.

(또한, 앱의 개수의 범위는 1 <= N <= 100, 각 앱을 비활성화 했을 경우의 비용의 범위는 1 <= c <= 100 이기 때문에 메모리는 충분하다.)

import sys


si = sys.stdin.readline

# Tabulation
def preprocess():
    for i in range(1, n + 1):
        for j in range(10001):
        	# i번째 앱의 비용이 j 보다 클 경우 
            if cost[i] > j:
            	# i번째 앱은 고를 수 없다. 
                dp[i][j] = dp[i - 1][j]
            # i번째 앱의 비용이 j 보다 같거나 작을 경우
            else:
            	# i번째 앱을 고르지 않은 경우와, 고른 경우 중 확보할 수 있는 메모리가 더 큰 쪽으로 점화식을 갱신 
                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - cost[i]] + memory[i])


def solution():
    for j in range(10001):
    	# n 개의 앱을 모두 고려한 경우, 
        # 가장 적은 양의 비용(j)으로 m 이상의 메모리를 확보할 수 있는 경우를 찾음 
        if dp[n][j] >= m:
        	# 찾았다면 그것이 원하는 값(주어진 메모리를 확보할 수 있는 최소 비용) 
            print(j)
            return


n, m = map(int, si().split())
memory = [0] + list(map(int, si().split()))
cost = [0] + list(map(int, si().split()))


# dp[i][j] -> i번째 인덱스의 앱까지 고려했을때 비용 j 만큼 사용하여 얻을 수 있는 최대 메모리

# 10001로 설정해야 하는 이유:
# 각각의 비용은 범위는 1 ≤ c ≤ 100 이다
# 앱의 개수의 범위는 1 ≤ n ≤ 100 이다
# 따라서 비용의 총 합의 범위는 10000 이하이다.
# 미리 dp 배열의 모든 값을 채워버린 후에 원하는 값(답)을 찾는 방식이므로 
# 배열의 범위(최대 값)를 찾는게 중요하다.
dp = [[0 for _ in range(10001)] for _ in range(n + 1)]

preprocess()
solution()

문제의 요구 조건은 'm 만큼의 메모리를 확보하기 위한 최소 비용 c 를 구하는 것'이지만(진짜 문제),

이를 뒤집어 '주어진 i개의 앱을 모두 고려하여 비용을 j 만큼 사용 할 때, 얻을 수 있는 최대 메모리'라고 문제를 다시 정의(가짜 문제)하여 문제를 풀이 할 수 있었다.

메모리를 m 이상 확보할 수 있는 비용 j가 존재한다면, 그 j 들 중 가장 작은 값이 c 이기 때문이다.