https://school.programmers.co.kr/learn/courses/30/lessons/150367
취약 유형...
트리문제의 풀이 과정을 블로그에 적어보며 그 풀이 과정을 곱씹어보도록 하겠다.
풀이한 코드는 다음과 같다.
# binary 라는 이진수의 L 인덱스 부터 R 인덱스 까지가 올바르게 포화 이진트리를 형성할 수 있는지 확인
# 시간 복잡도 O(n), n -> 트리의 노드 수
def solve(binary, L, R):
# 리프 노드까지 도달(포화 이진트리로 표현 가능)
if L == R:
return True
# 현재 트리의 루트 인덱스 계산
mid = (L + R) // 2
root = binary[mid]
# 왼쪽 자식의 인덱스
left_child = binary[(L + (mid - 1)) // 2]
# 오른쪽 자식의 인덱스
right_child = binary[((mid + 1) + R) // 2]
# 루트가 0인데 자식이 1인 경우 False 반환(포화 이진트리로 표현 불가능)
if left_child == '1' and root == '0':
return False
if right_child == '1' and root == '0':
return False
# 왼쪽 하위 트리, 오른쪽 하위 트리 확인
return solve(binary, L, mid - 1) and solve(binary, mid + 1, R)
def solution(numbers):
answer = []
for elem in numbers:
# 2진수로 변환 ('0b' 제거)
# print("binary", bin(elem))
# binary 0b111
binary = bin(elem)[2:]
# print("binary", binary)
# binary 111
tree_size = 1
# 이진 트리의 크기를 숫자의 길이에 맞게 조정
# 1 -> 3 -> 7 -> 15...
# print("len(binary)", len(binary))
while tree_size < len(binary):
tree_size = tree_size * 2 + 1
# print("tree_size", tree_size)
# 이진 숫자 앞에 '0' 을 추가하여 올바른 트리의 크기와 일치시킴(더미 노드 추가)
# 111 -> 0000111
binary = '0' * (tree_size - len(binary)) + binary
# print("binary", binary)
# print()
# 이진 트리인지 확인
if solve(binary, 0, len(binary) - 1):
answer.append(1)
else:
answer.append(0)
return answer
# print(solution([7, 42, 5]))
# print(solution([63, 111, 95]))
우선 python 의 내장 함수인 bin()함수를 통해 입력받은 10진수를 2진수로 변환해주도록 한다.
단, bin 을 통해 숫자를 변환하면 prefix 로 '0b' 가 붙기때문에 이를 제거하기 위해 [2:] 를 통해 slicing 을 해주었다.
for elem in numbers:
binary = bin(elem)
print(binary)
# numbers = [7, 42, 5]
# 0b111
# 0b101010
# 0b101또한 포화 이진 트리 형태의 2진수가 되도록 만들어주기 위해
더미노드를 채우는 과정을 코드로 표현해보았다.
for elem in numbers:
# 입력받은 숫자(10진수)를 2진수로 변환
binary = bin(elem)[2:]
tree_size = 1
# 포화 이진트리의 형태가 되도록 2진수 변환
while tree_size < len(binary):
tree_size = tree_size * 2 + 1
binary = '0' * (tree_size - len(binary)) + binary
tree의 사이즈를 1로 초기화 해준 다음
무한 루프를 통해 변환한 2진수의 길이 보다 크거가 같은 첫번째 포화 이진트리의 노드의 개수를 구한다.
포화 이진트리는 각 노드에 자식 노드가 2개씩 달려있기 때문에 depth가 증가할 수록 전체 노드의 개수는 다음과 같은 점화식을 만족한다
f(n) = 2* f(n-1) + 1 (n >= 1)
tree의 size 를 찾았다면 문자열을 보정하기 위해 tree_size - 2진수의 문자열의 길이 만큼의 0을 앞쪽에 채워주도록 한다.
tree의 size와 숫자를 2진수로 변환한 문자열의 길이가 같으면 앞에 0을 붙혀주지 않는다.
지금까지가 문제를 풀기 위한 전처리 였고 지금부터가 문제 풀이이다.
보정한 문자열이 이진트리의 형태를 만족하는 검사하여 이진트리의 형태가 맞다면 1, 아니면 0을 결과로 산출해내야 한다.
이를 코드로 구현한 것이 solve 함수이다.
# binary 라는 이진수의 L번지 부터 R번지 까지가 올바르게 포화 이진트리로 표현되느냐?
def solve(binary: str, L: int, R: int) -> bool:
# L과 R이 같다 -> 루트 노드에 도달하였다
# 이는 포화 이진트리로 표현이 가능하다.
if L == R:
return True
# L과 R의 중간 인덱스인 mid 를 구한다
mid = (L + R) // 2
# 해당 인덱스의 원소를 root 라고 했을때,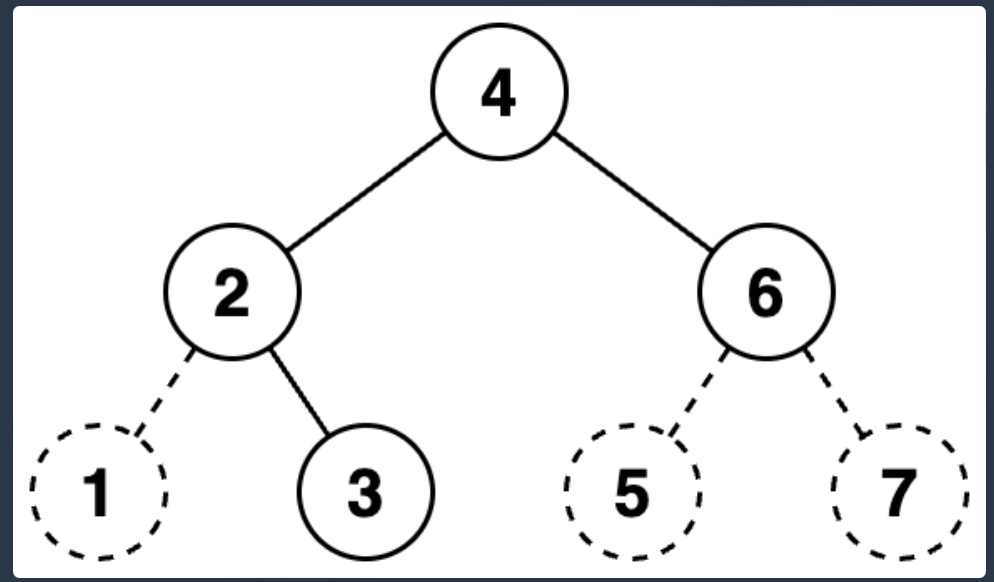
root = binary[mid]
# root 의 왼쪽 노드의 인덱스
left_child = binary[(L + (mid - 1)) // 2]
# root 의 오른쪽 노드의 인덱스
right_child = binary[((mid + 1) + R) // 2]
# left child가 1인데(채워져있는데), root가 0이라면(채워져있지 않다면)
# 이진트리의 형태를 만족시키지 못한다
if left_child == '1' and root == '0':
return False
# right child가 1인데(채워져있는데), root가 0이라면(채워져있지 않다면)
# 이진트리의 형태를 만족시키지 못한다
if right_child == '1' and root == '0':
return False
# 이진 트리의 형태를 만족한다면
# R 을 mid-1 로 하는, L 을 mid + 1로 하는 판별을 재귀적으로 수행
return solve(binary, L, mid - 1) and solve(binary, mid + 1, R)solve 함수에서는 현재 검사를 하는 binary 라는 문자열과 이 문자열의 첫번째, 마지막 인덱스가 parameter 로 들어간다.
