Today I Learned
오늘은 그래프에 대하여 정리하고, 그래프를 탐색하는 알고리즘에 대하여 정리해 보았다.
그래프
그래프는 노드와, 노드와 노드 사이를 연결해주는 간선으로 이루어진 비선형 자료구조이다.
그래프의 특징과 트리와 비교
- 정점은 여러 개의 자식을 가질 수 있다.
- 그래프의 간선은 방향성을 가질 수 있고(갖지 않을 수도 있다), 가중치를 가질 수 있다.
- 트리와는 달리, 사이클을 가질 수 있다.
그래프의 표현
그래프는 크게 두 가지 표현법이 있다. (물론 더 있을 수도 있다)
- 인접 리스트 (adjacent list)
- 인접 행렬 (adjacent matrix)
인접 리스트와 인접 행렬
인접 리스트는 다음과 같이 표현한다.
// adj[from][to] 형식의 인덱스로 나타낼 수 있다.
const adjacentList: Array<Array<number>> = [
[],
[2, 4],
[1, 3],
[1, 2],
[3],
[],
];이 표현은 간선 (u, v)를 탐색하기 위해서는 O(n)의 시간이 소요되지만, 모든 노드에 대하여 탐색할 때에는 더 유리할 수 있다. 그리고 기본적으로 메모리를 덜 쓴다.
인접 행렬은 다음과 같이 표현한다.
/* adj[from][to] 형식의 인덱스로 나타낼 수 있다.
* 연결된 간선은 1로, 그렇지 않으면 0으로 표현한다.
*/
const adjMatrix: Array<Array<number>> = [
[0, 1, 0, 0, 0],
[1, 0, 1, 1, 0],
[0, 1, 0, 0, 0],
[0, 1, 0, 0, 1],
[0, 0, 0, 1, 0],
];이 표현은 간선 (u, v)를 O(1)의 시간으로 탐색할 수 있다는 것이 장점이지만, 노드의 개수가 많아질 수록 많은 메모리를 차지한다. 따라서 상황에 따라 적절하게 사용하는 것이 좋다.
그래프 탐색 알고리즘
- 방향성이 없는 경우:
- Union-find
- 간선에 가중치가 있는 경우:
- 플로이드-워셜
- 다익스트라
- 크러스컬 (최소 스패닝 트리)
- ...
- 그 외 범용적으로 사용할 수 있는 것들
- dfs(깊이 우선 탐색)
- bfs(너비 우선 탐색)
모든 그래프 탐색 알고리즘의 기초는 동일하므로, 원리에 대해서만 정리하고, 나머지는 추후에 정리하도록 한다.
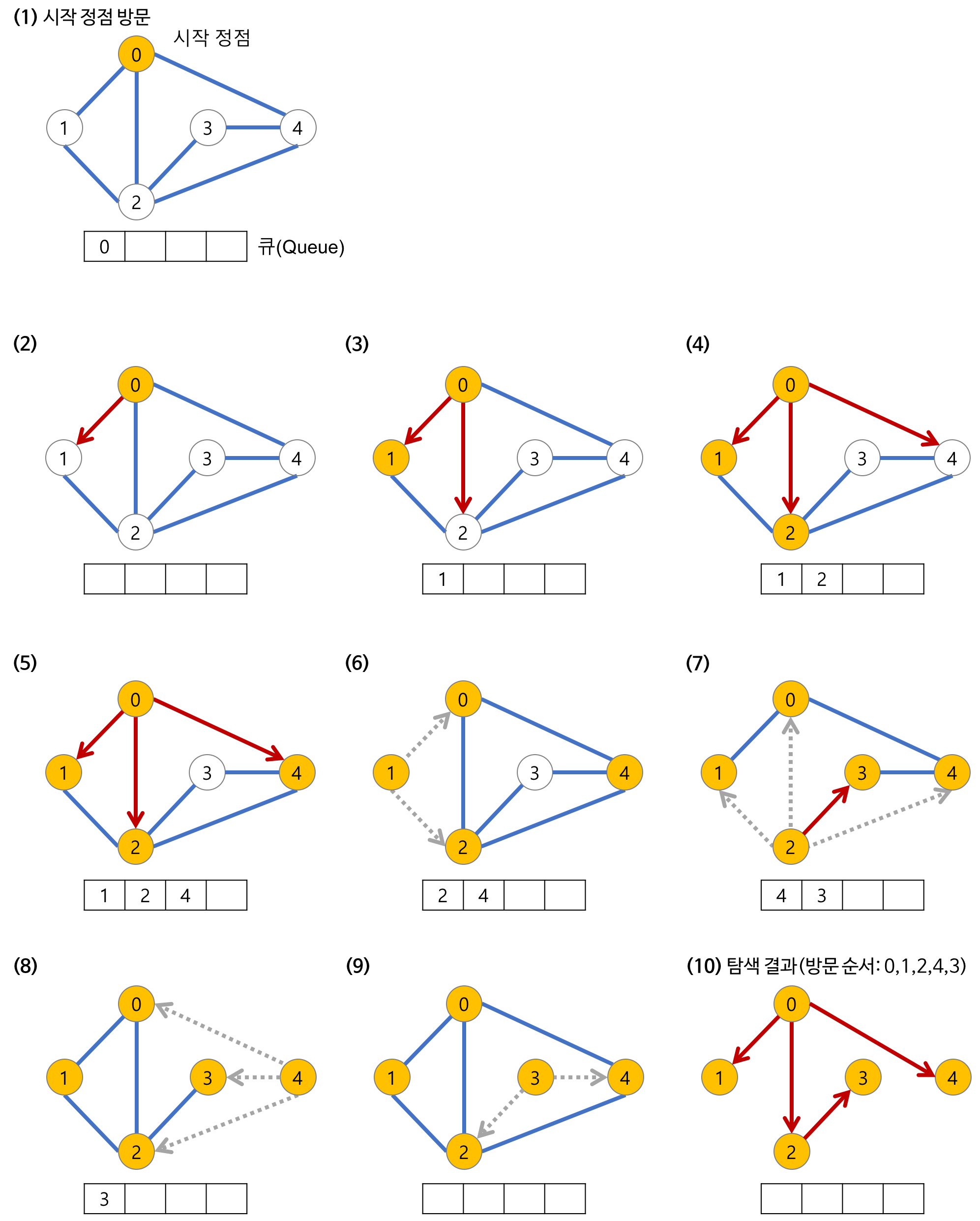
다음은 너비 우선 탐색의 원리를 나타낸 것이다.
1. 첫 노드를 방문한다.
2. 현재 위치의 노드와 간선으로 연결된 모든 이웃 노드들을 탐색한다.
3. 탐색 결과 아직 방문하지 않은 이웃 노드들이 존재한다면, 방문 처리를 해 준 후, 다음 노드를 방문한다.
그림을 보면 알 수 있는 중요한 점은, 아무리 그래프의 간선이 많더라도, 그래프 탐색 알고리즘을 통해 방문한 간선들을 연결해 주면, 스패닝 트리가 만들어진다는 것이다.
BFS, DFS의 시간 복잡도
일반적으로 가장 많이 사용되는 BFS, DFS의 시간복잡도는 인접 리스트로 표현되었다면 O(V(노드의 개수) + E(간선의 개수))의 시간복잡도를 가진다. 인접 행렬로 표현되었다면 O(N^2)의 시간복잡도를 가진다.
구현의 복잡도는 시스템 스택을 이용하는 dfs와 달리 bfs는 재귀적이지 않고 Queue 자료구조를 이용하므로, 조금 더 복잡할 수는 있으나, 아무리 많은 노드를 탐색하더라도 스택오버플로우가 발생하지 않아 메모리 측면에서는 더 도움이 될 수 있다.
