문제 출처

단계별로 풀어보기 > 약수와 배수와 소수 2 > 가로수
https://www.acmicpc.net/problem/2485

문제 설명

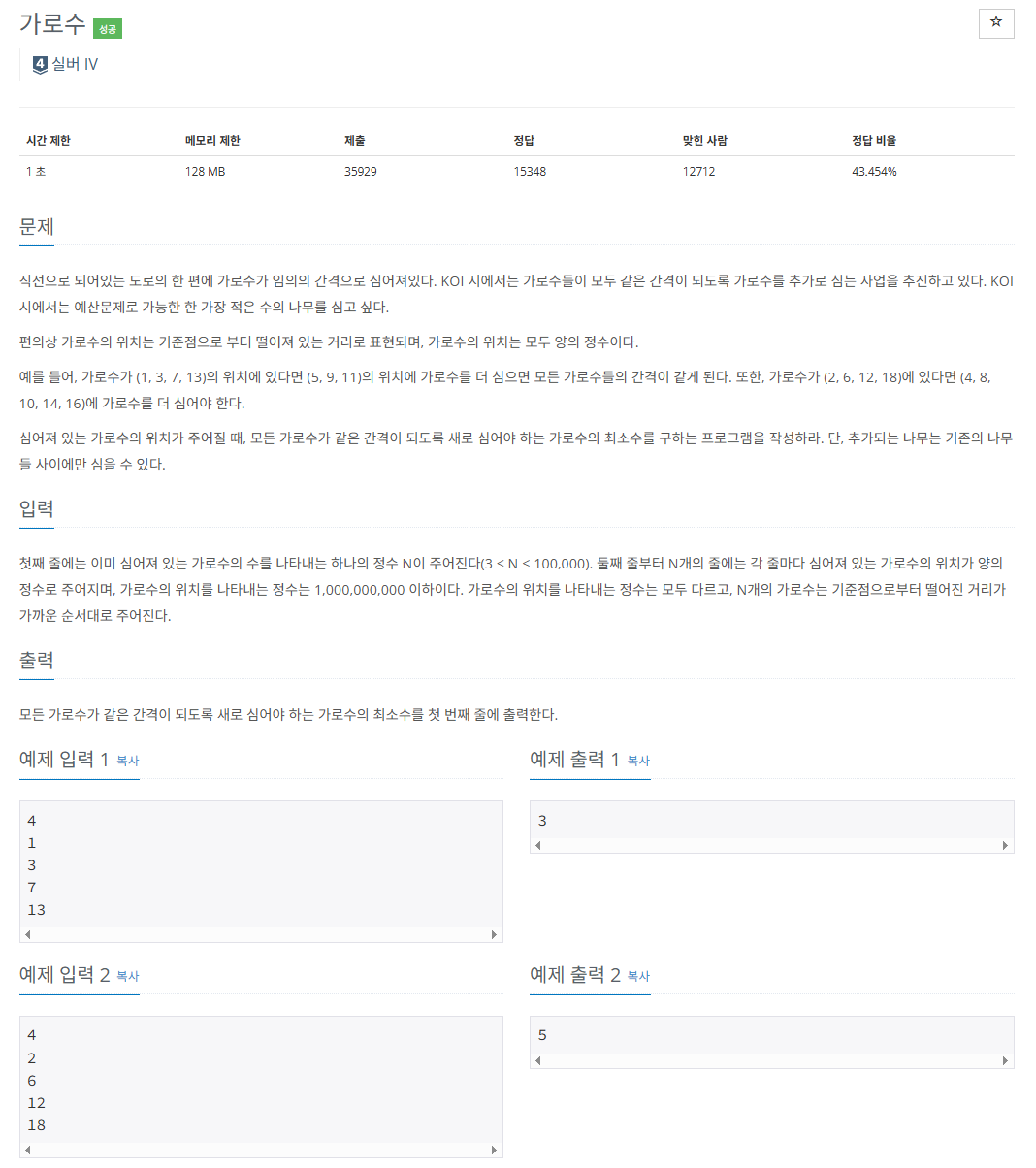
가로수의 갯수와 각 가로수의 위치가 주어질 때, 가로수들이 모두 같은 간격이 되도록 가로수를 추가로 심는다. 이 때, 필요한 가로수의 갯수를 구하여라

접근 방법

가로수들 간격 사이의 최대공약수(GCD)를 이용하여 간격의 크기에서 최대공약수를 나누고 1을 빼는 방식으로 각 간격에 필요한 가로수를 구했다.

import java.io.*;

public class 가로수 {

    public static int GCD(int a, int b){
        while(b != 0){
            int temp = b;
            b = a % b;
            a = temp;
        }
        return a;
    }

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

        int N = Integer.parseInt(br.readLine());

        int arr[] = new int[N];

        for(int i = 0; i < N; i++){
            arr[i] = Integer.parseInt(br.readLine());
        }
        int gcd = arr[1]-arr[0];

        for(int i = 1; i < N-1; i++){
            gcd = GCD(gcd,arr[i+1]-arr[i]);
        }

        int count = 0;

        for(int i = 0; i < N-1; i++){
            count += (arr[i+1] - arr[i])/gcd - 1;
        }

        bw.write(String.valueOf(count));
        bw.flush();
        bw.close();
        br.close();

    }
}

알게된 점

마지막 for문을 사용하지 않고, 첫번째 가로수와 마지막 가로수의 간격을 구한다음 최대공약수로 나누고, 현재 있는 가로수의 갯수를 빼서 필요한 가로수의 갯수를 알아내는 방식도 있다.

시간 복잡도는 가로수의 갯수 N 개를 3번 순회 했으므로, O(3N) -> O(N)이 된다.

문제푼 흔적