문제 출처

단계별로 풀어보기 > 누적 합 > 구간 합 구하기 5
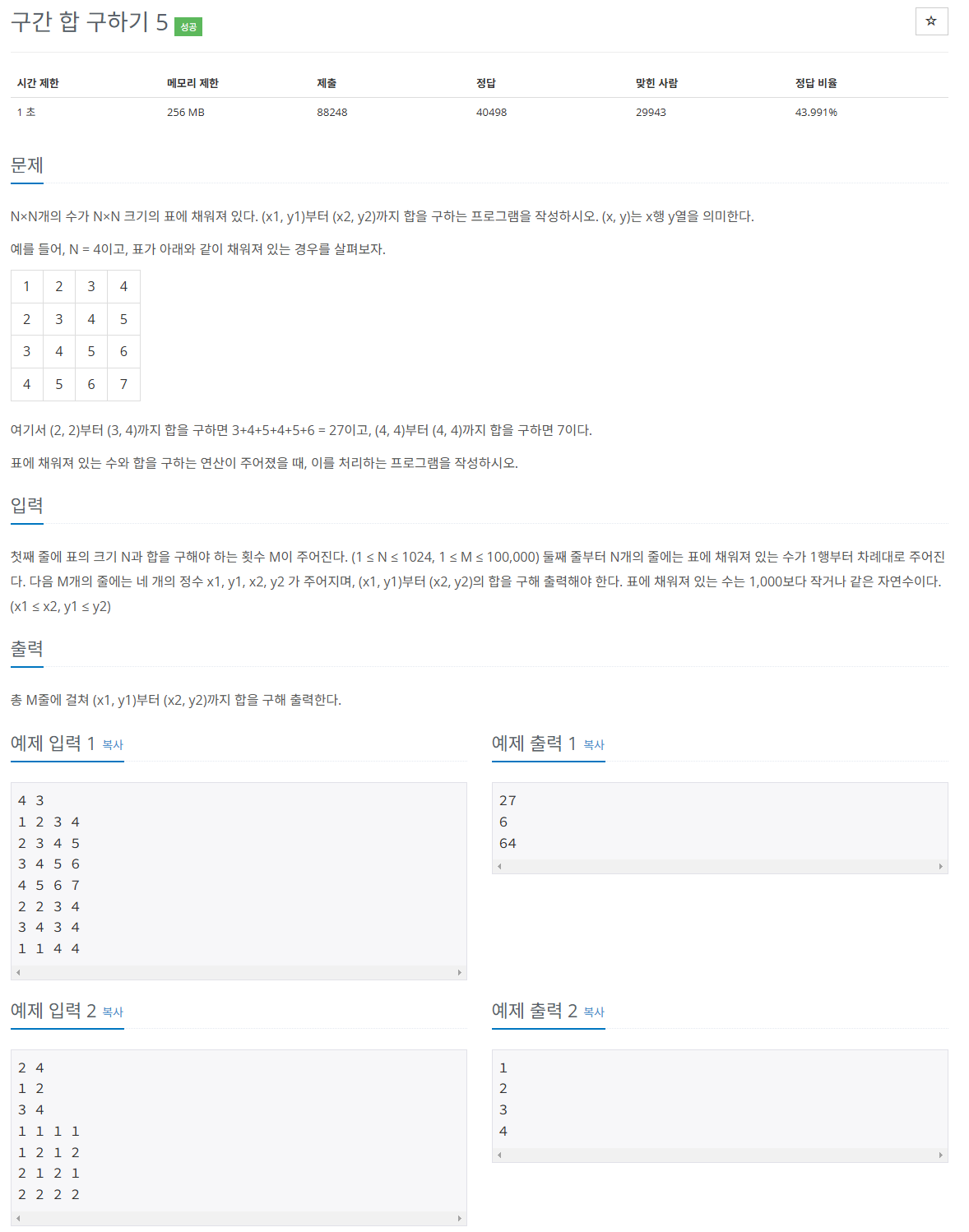
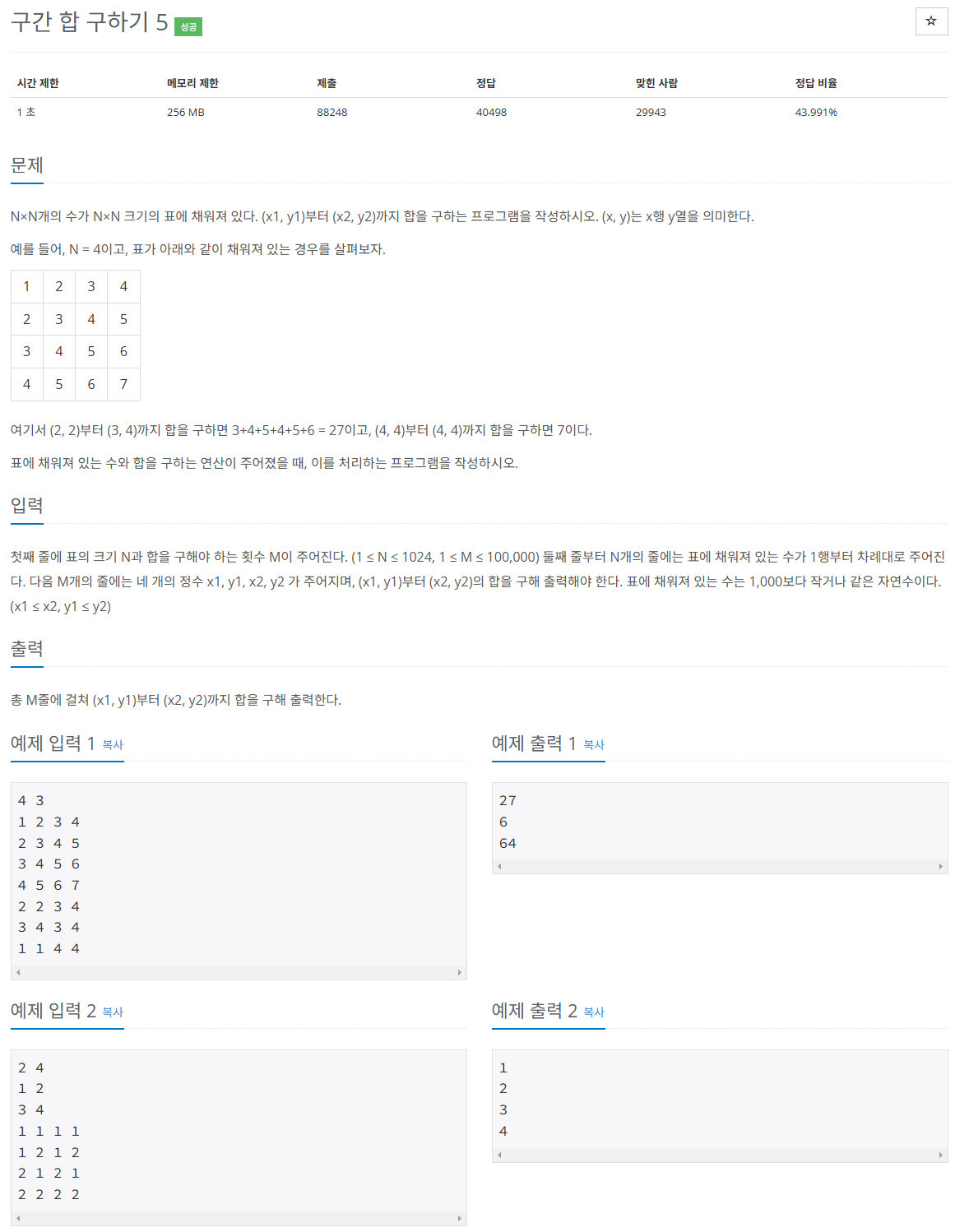
https://www.acmicpc.net/problem/11660

문제 설명

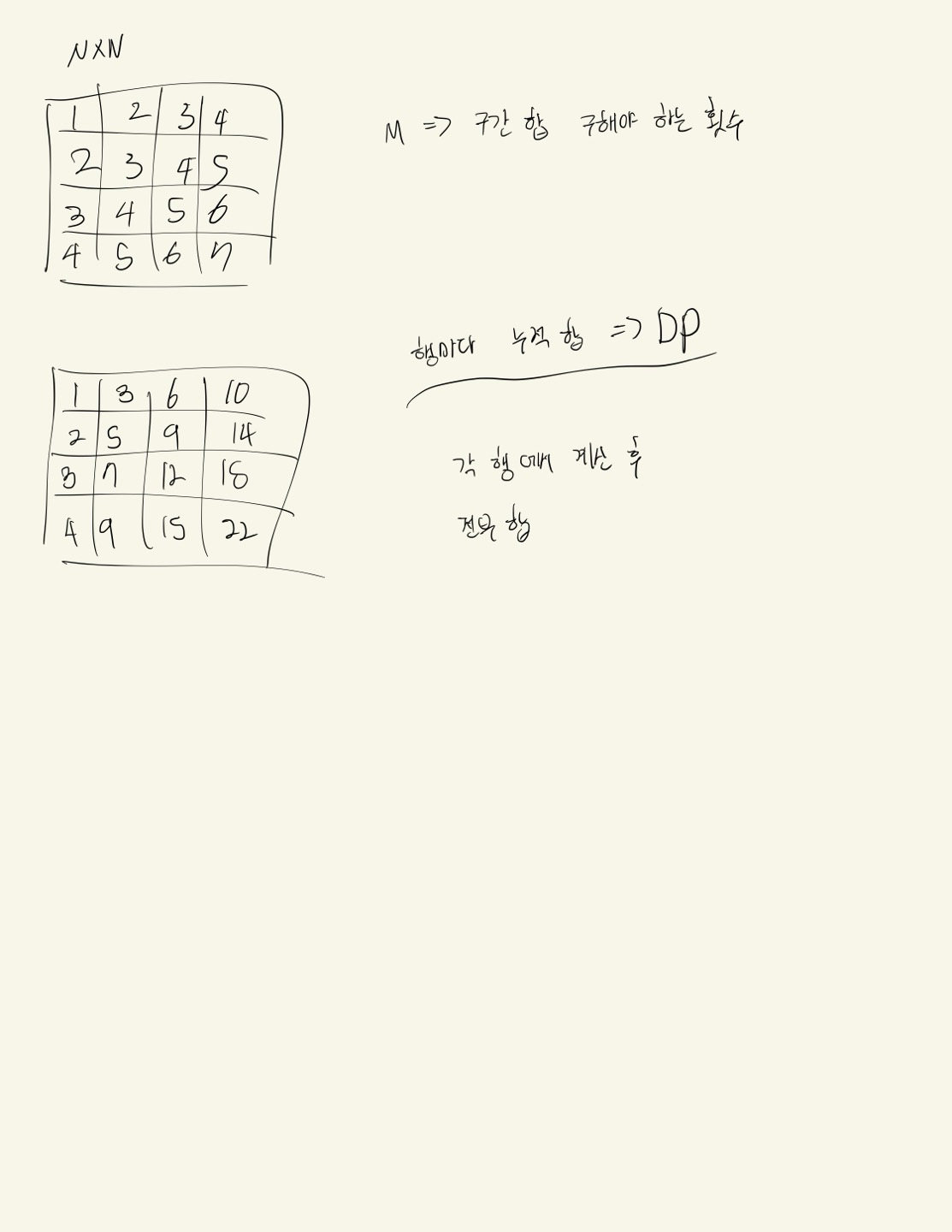
표의 크기를 정하는 N(표의 크기 = N * N),
구간을 주는 횟수 M이 주어질 때,
주어진 각 구간에 따라 표의 누적합을 구하라.

접근 방법

해당 문제는 다이나믹 프로그래밍을 이용하여 풀이한다.
N*N의 표를 생성할 때, 각 행마다 2번 열에는 2번열에 들어가는 값 + 그 전 열까지의 누적 합, 3번 열에는 3번 열에 들어가는 값 + 그 전 열까지의 누적 합으로 표를 생성한다.

이 후, 값을 도출 할 때는
주어진 구간의 각 행의 마지막 열 값 - 구간 각 행의 처음 이전의 값을 합하여 구한다.

import java.io.*;
import java.util.ArrayList;
import java.util.List;
import java.util.StringTokenizer;

public class 구간_합_구하기_5 {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        StringTokenizer st = new StringTokenizer(br.readLine());

        int N = Integer.parseInt(st.nextToken());
        int M = Integer.parseInt(st.nextToken());

        int[][] graph = new int[N+1][N+1];

        for(int i = 1; i<N+1; i++){
            st = new StringTokenizer(br.readLine());
            for(int j = 1; j<N+1; j++){
                graph[i][j] = graph[i][j-1]+ Integer.parseInt(st.nextToken());
            }
        }


        for(int k = 1; k<=M; k++){
            int sum = 0;
            st = new StringTokenizer(br.readLine());
            int x1 = Integer.parseInt(st.nextToken());
            int y1 = Integer.parseInt(st.nextToken());
            int x2 = Integer.parseInt(st.nextToken());
            int y2 = Integer.parseInt(st.nextToken());

            for(int l = x1; l<=x2; l++){
                sum += graph[l][y2] - graph[l][y1-1];
            }
            bw.write(String.valueOf(sum) + "\n");
            bw.flush();
        }
        bw.close();
        br.close();
    }
}

Review

import java.io.*;
import java.nio.Buffer;
import java.util.StringTokenizer;

public class 구간_합_구하기_5_review {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        StringTokenizer st = new StringTokenizer(br.readLine());

        int N = Integer.parseInt(st.nextToken());
        int M = Integer.parseInt(st.nextToken());

        int[][] graph = new int[N+1][N+1];

        // 누적 합 그래프 형성
        for(int i = 1; i<=N; i++){
            st = new StringTokenizer(br.readLine());
            for(int j = 1; j<=N; j++){
                graph[i][j] = graph[i][j - 1] + Integer.parseInt(st.nextToken());
            }
        }



        for(int k = 0; k<M; k++){
            int sum = 0;

            st = new StringTokenizer(br.readLine());

            int x1 = Integer.parseInt(st.nextToken());
            int y1 = Integer.parseInt(st.nextToken());
            int x2 = Integer.parseInt(st.nextToken());
            int y2 = Integer.parseInt(st.nextToken());

            for(int l = x1; l<=x2; l++){
                sum += graph[l][y2] - graph[l][y1-1];
            }
            bw.write(sum + "\n");
            bw.flush();
        }
        bw.close();
        br.close();
    }
}

알게된 점

처음 문제를 풀이할 때는, 단순히 주어진 구간에 대해서 계속 더하는 방식을 사용하여 시간 복잡도가 O(n^3)이 나와서 시간 초과했다.
하지만 다이나믹 프로그래밍 방법으로 접근하면 O(n^2)이 된다.

import java.io.*;
import java.util.ArrayList;
import java.util.List;
import java.util.StringTokenizer;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        StringTokenizer st = new StringTokenizer(br.readLine());

        int N = Integer.parseInt(st.nextToken());
        int M = Integer.parseInt(st.nextToken());

        int[][] graph = new int[N][N];

        for(int i = 0; i<N; i++){
            st = new StringTokenizer(br.readLine());
            for(int j = 0; j<N; j++){
                graph[i][j] = Integer.parseInt(st.nextToken());
            }
        }

        List<int[]> panel = new ArrayList<>();

        for(int k = 0; k<M; k++){
            st = new StringTokenizer(br.readLine());
            int[] arr = new int[4];
            for(int l = 0; l<4; l++){
                arr[l] = Integer.parseInt(st.nextToken());
            }
            panel.add(arr);
        }



        for(int[] m : panel){
            int count = 0;
            int startX = m[0];
            int endX = m[2];
            int startY = m[1];
            int endY = m[3];

            for(int n = startX-1; n<endX; n++){
                for(int o = startY-1; o<endY; o++){
                    count +=graph[n][o];
                }
            }

            bw.write(String.valueOf(count) + "\n");
            bw.flush();
        }
        bw.close();
        br.close();
    }
}

문제푼 흔적

Review