문제 출처

단계별로 풀어보기 > 이분 탐색 > 나무 자르기
https://www.acmicpc.net/problem/2805

문제 설명

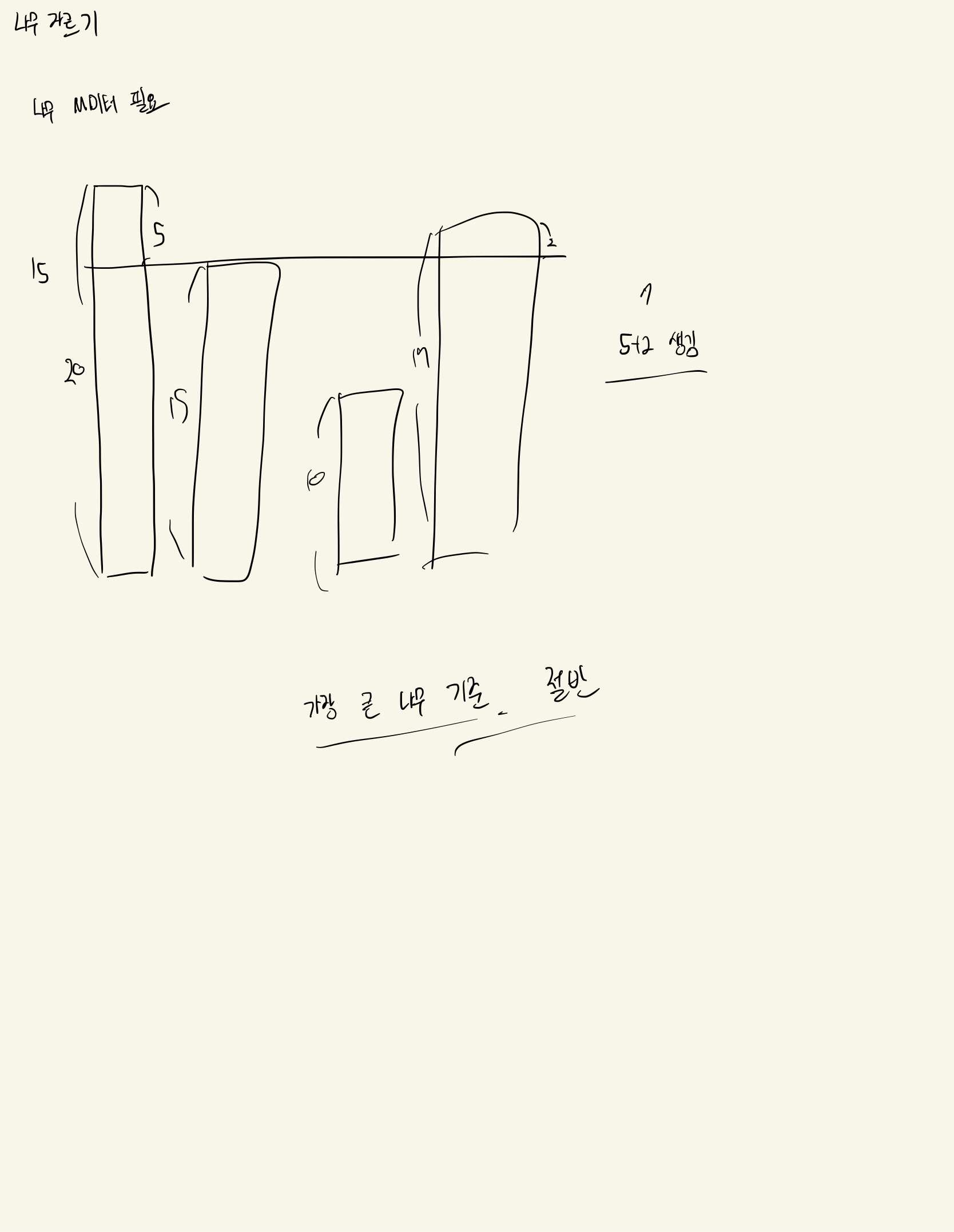
나무 M미터가 필요할 때, 나무 절단기를 H미터로 설정하여 나무를 잘라 필요한 나무를 마련한다. 이 때, 나무의 수와 필요한 나무 M미터의 수가 주어지면 절단기에 설정할 수 있는 높이의 최댓값을 출력하라.

접근 방법

이분 탐색을 통해 풀이한다.
배열에 각 나무의 길이를 저장하고, 가장 큰 나무의 길이를 high, 나무의 최소 길이 1을 low로 설정한다. 이 후, mid를 설정하고, 그 mid와 각 나무 길이를 비교하여 더한 후, 원하는 값과 비교했을 때, 크다면 절단기 높이를 더 높게하기 위해서 low = mid +1, 작다면 절단기 높이를 더 작게하기 위해서 high = mid - 1로 설정한다.

import java.io.*;
import java.util.StringTokenizer;

public class 나무_자르기 {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

        StringTokenizer st = new StringTokenizer(br.readLine());
        int N = Integer.parseInt(st.nextToken());
        long T = Long.parseLong(st.nextToken());

        int[] arr = new int[N];

        st = new StringTokenizer(br.readLine());

        int low = 1;
        int high = 0;
        int mid = 0;


        for(int i = 0; i < N; i++){
            arr[i] = Integer.parseInt(st.nextToken());
            high = Math.max(arr[i], high);
        }

        while(low <= high){
            mid = (low + high) / 2;
            long sum = 0;
            for(int i = 0; i < N; i++){
                if(arr[i] - mid >= 0) sum += (arr[i] - mid);
            }

            if(sum < T) high = mid-1;
            else if (sum >= T) low = mid+1;
        }
        bw.write(String.valueOf(high));
        bw.flush();
        bw.close();
        br.close();

    }
}

알게된 점

처음 풀이할 때, 조건을 반대로 설정했었다. 답에 대해서 좀 더 깊게 생각해야한다.

시간 복잡도는 배열 순회 + 가장 큰 나무의 길이 인 O(N log(maxHeight))가 나온다.

문제푼 흔적