문제 출처

코딩테스트 연습 > 동적계획법(Dynamic Programming) > 등굣길
https://school.programmers.co.kr/learn/courses/30/lessons/42898

문제 설명

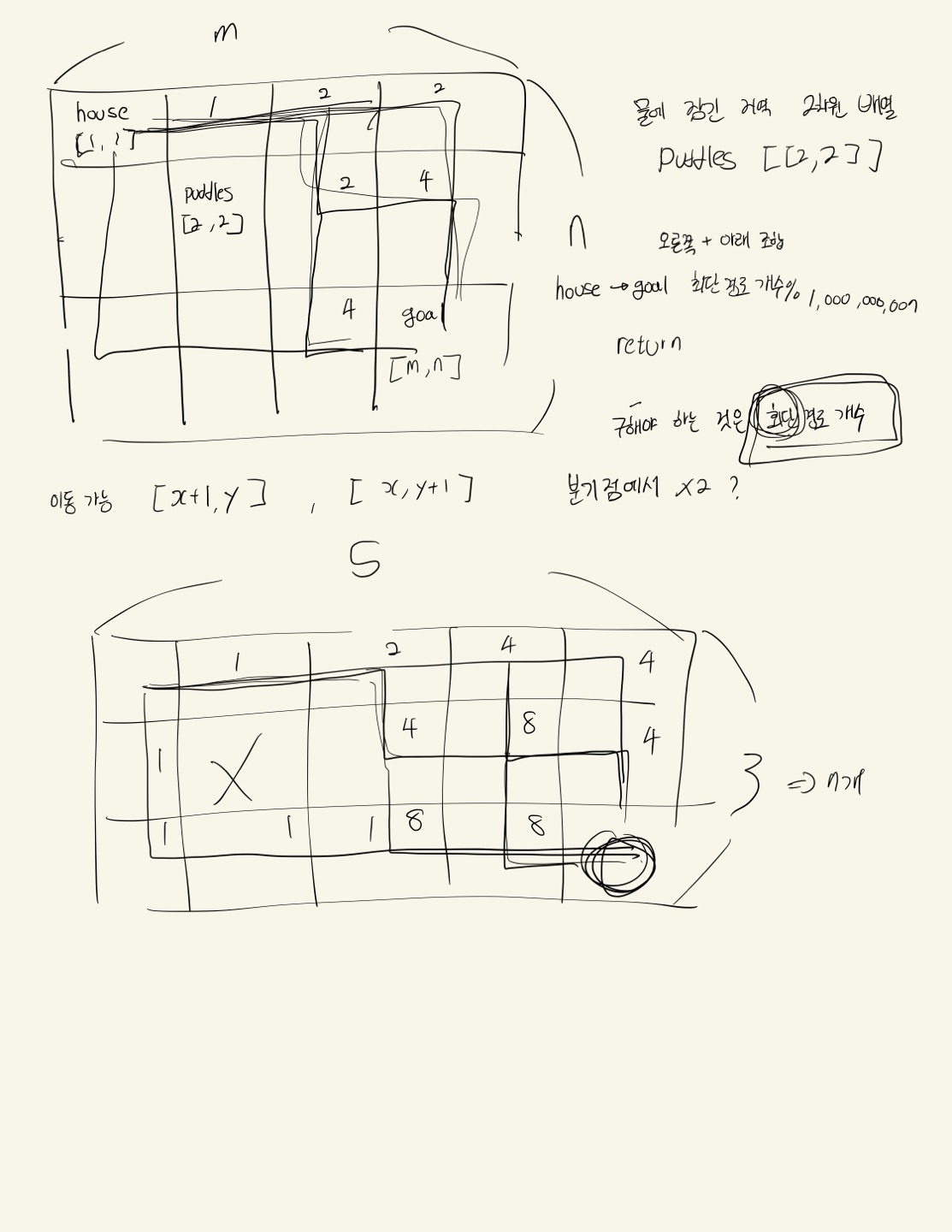
n x m 격자(문제 상 오류) 가 주어지고, 지나갈 수 없는 지역의 2차원 배열 puddles가 주어질 때, 집(1,1)에서 학교(n,m)까지 가는 최단 경로의 수 % 1,000,000,007 를 return하라.

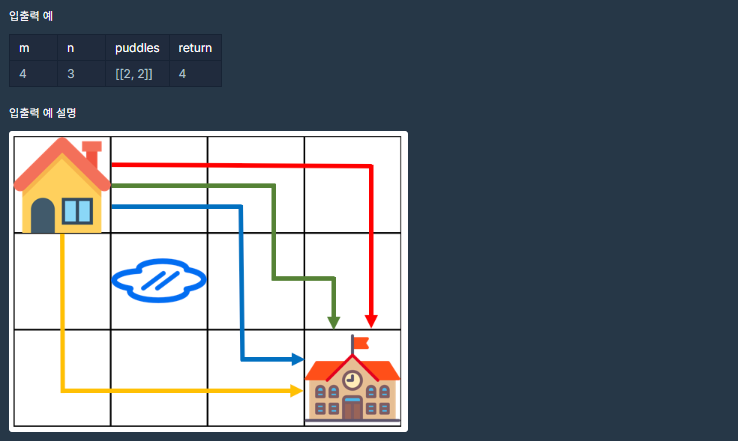
접근 방법

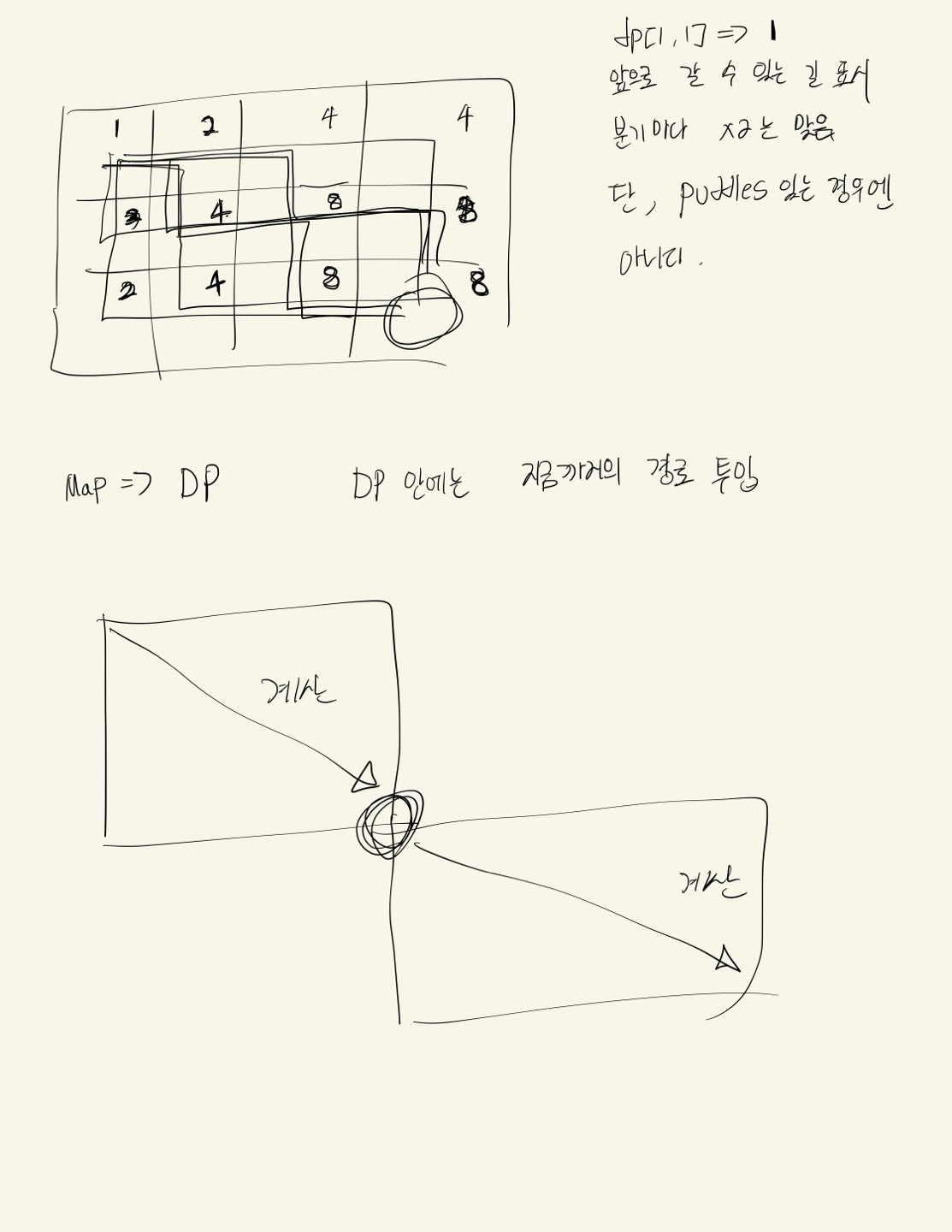
n x m 을 2차원 배열 dp로 나타내고, puddles 배열 안의 웅덩이 위치를 -1로 표시한다.

dp에서 현재 위치의 경로 dp[i][j]라 가정 할 때,
dp[i][j] = dp[i-1][j] + dp[i][j-1]이 된다.

이 때, 인덱스 범위와, dp[i-1][j] 가 -1인 경우, dp[i][j-1] 가 -1인 경우를 주의하여 마지막 까지 계산하면 된다.

class Solution {
    public int solution(int m, int n, int[][] puddles) {
        int mod = 1000000007;
        // Map 생성
        int[][] dp = new int[n][m];
        for(int[] k : puddles){ // Map 에 puddles 위치 -1 표기
            dp[k[1]-1][k[0]-1] = -1;
        }
        
        dp[0][0] = 1;
        // 현재 위치의 경로는 현재 x -1, y 의 경로 + 현재 x, y-1의 경로의 합
        
        for(int i = 0; i<n; i++){
            for(int j = 0; j<m; j++){
                if(dp[i][j] == -1) continue;
                
                if(j !=0){                
                    if(dp[i][j -1] != -1) dp[i][j] += dp[i][j-1] % mod;
                         }
                
                if(i !=0){                
                    if(dp[i-1][j] != -1) dp[i][j] += dp[i-1][j] % mod;
                }
                    }
            
            }
        return dp[n-1][m-1] % mod;
        }
        
    }

알게된 점

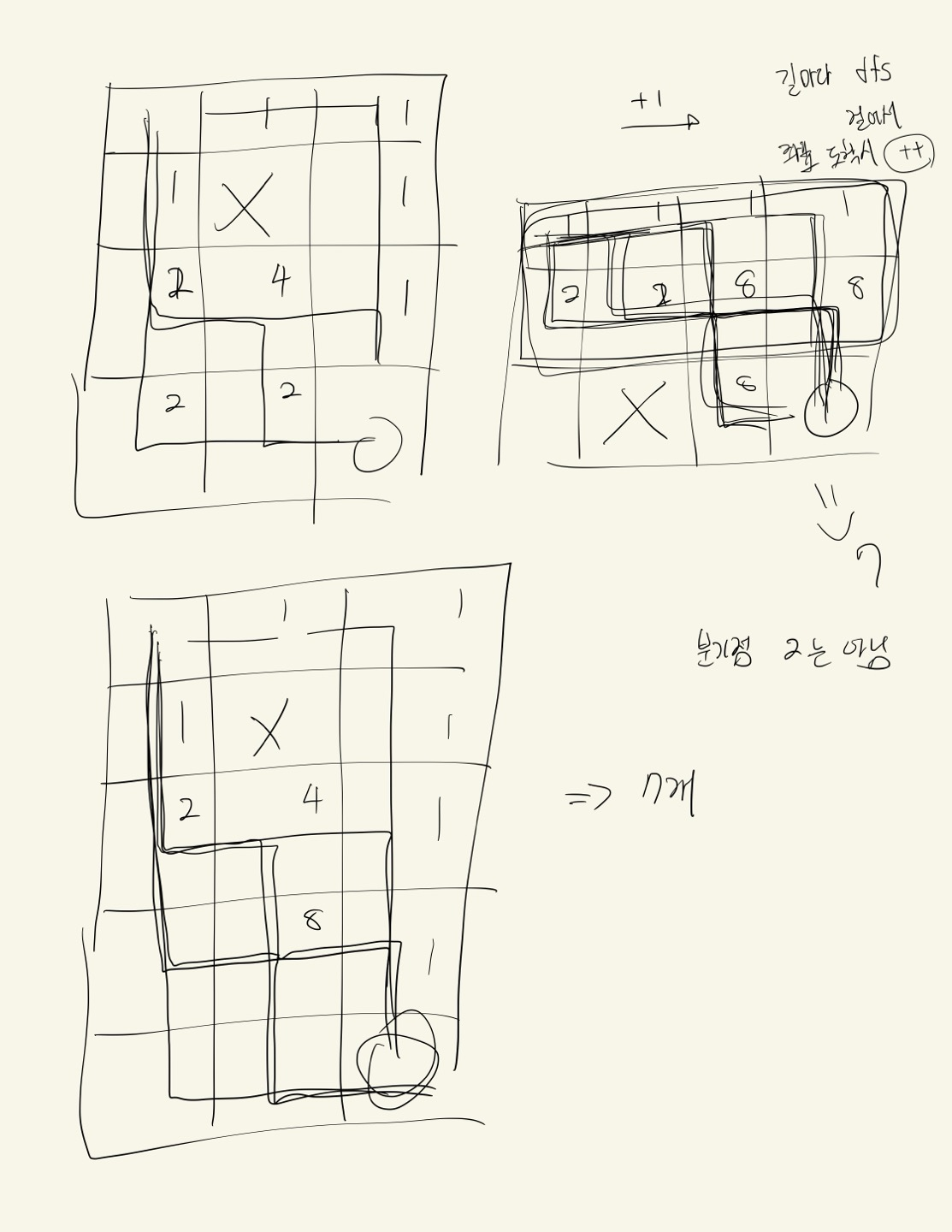
처음 문제를 접근할 때, 너무 어렵게 생각하여 현재 위치에서 다음으로 갈 수 있는 경우가 2가지 인 경우(분기가 나눠지는 경우) 현재까지 경로의 x2를 하는 방식을 생각했다.
하지만 이는 puddles가 생기면 계산이 틀린다.

간단하게 이전 경로들을 더하면 되는 문제였다.

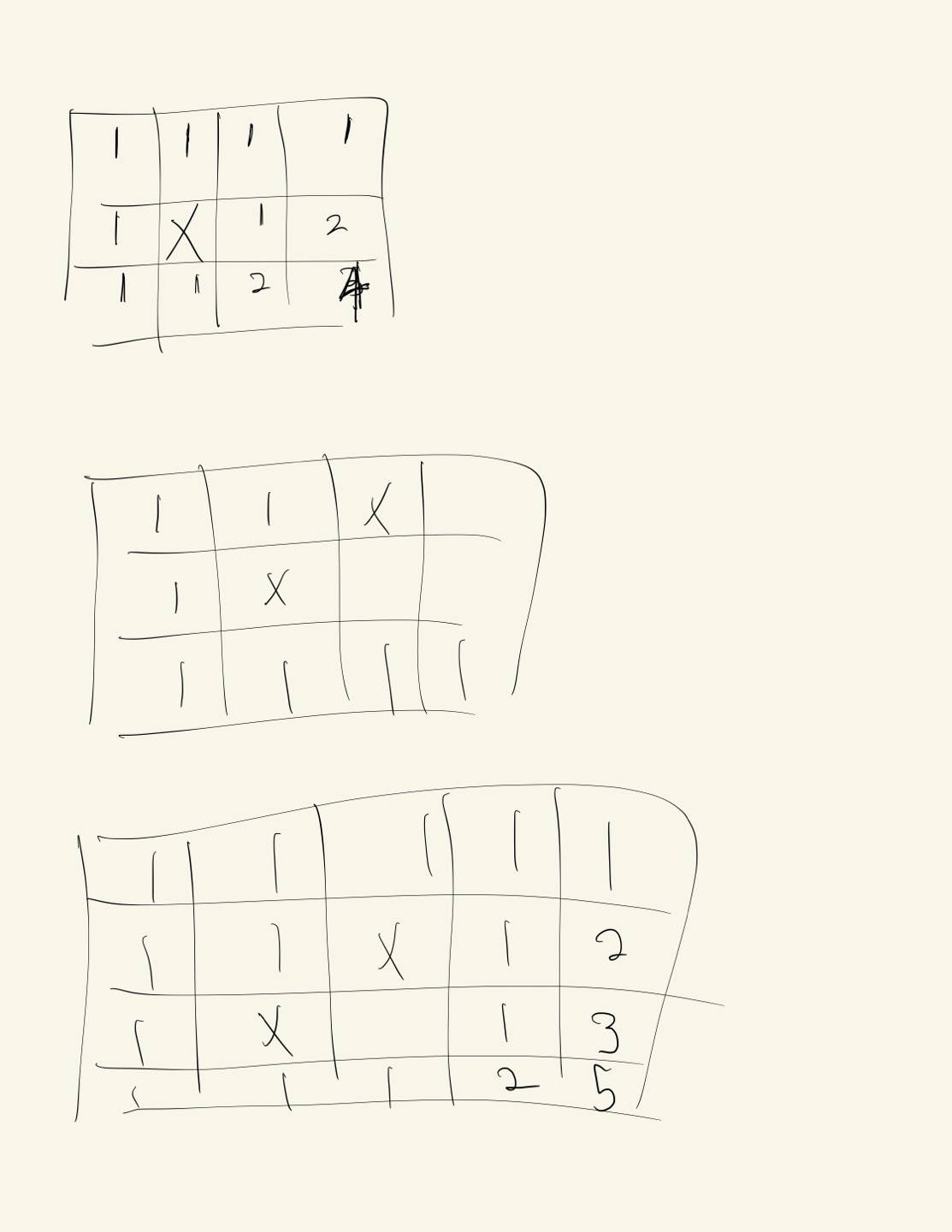
문제푼 흔적