[JAVA] 사칙연산

NoHae·2025년 3월 12일

프로그래머스_코딩테스트

목록 보기

45/51

문제 출처

https://school.programmers.co.kr/learn/courses/30/lessons/1843
코딩테스트 연습 > 동적계획법(Dynamic Programming) > 사칙연산

문제 설명

사칙연산에서 더하기는 결합 법칙을 성립하나, 빼기는 결합법칙이 성립하지 않는다.
숫자와 연산 기호가 문자열 형태로 들어가 있는 배열 arr가 주어질 때, 서로 다른 연산순서의 계산 결과 중 최댓값을 return 하라.

접근 방법

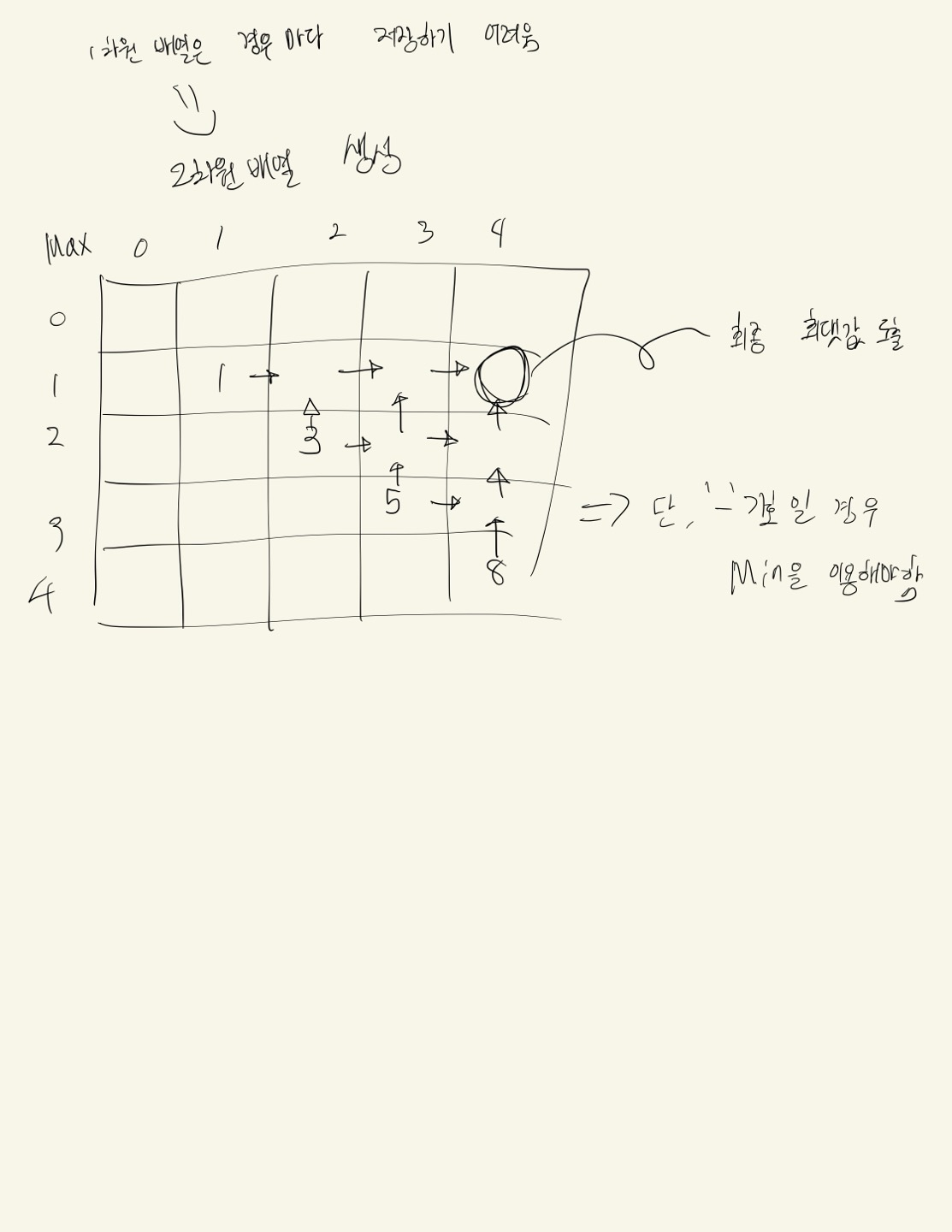
DP배열을 최댓값을 저장하는 maxDP, 최솟값을 저장하는 minDP 2개 만들어 생각한다.

"+" 기호 인 경우 어떤 경우가 최댓값, 최솟값 인지, "-"기호 인 경우 어떤 경우가 최댓값, 최솟값 인지를 알아야한다.

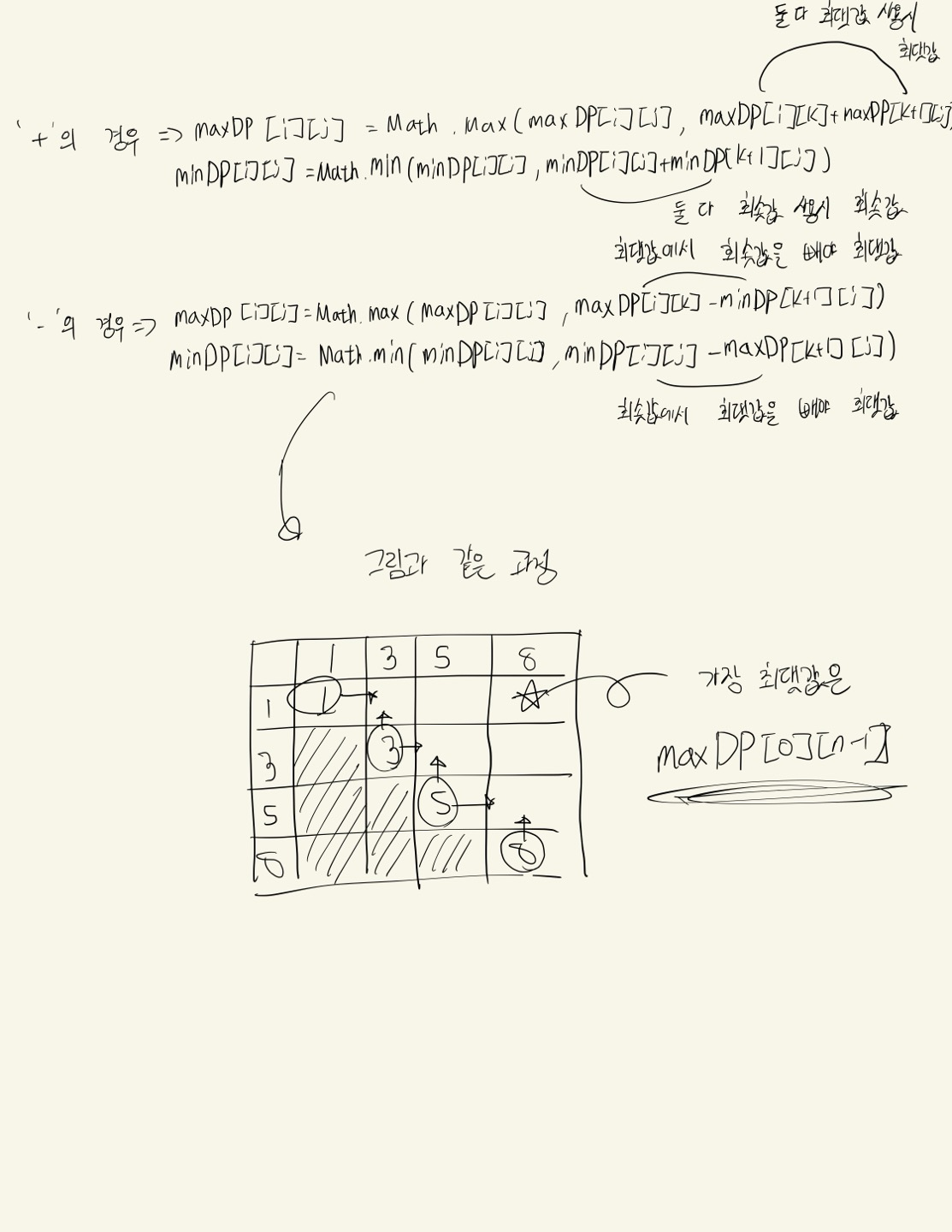
"+" 기호일 경우 최댓값은 (최댓값 + 최댓값)인 경우이고, 최솟값은 (최솟값 + 최솟값)이다.
"-" 기호일 경우 최댓값은 (최댓값 - 최솟값)인 경우이고, 최솟값은 (최솟값 - 최댓값)이다.

해당 경우를 각각 maxDP와 minDP에 저장하는 과정을 거치는데,
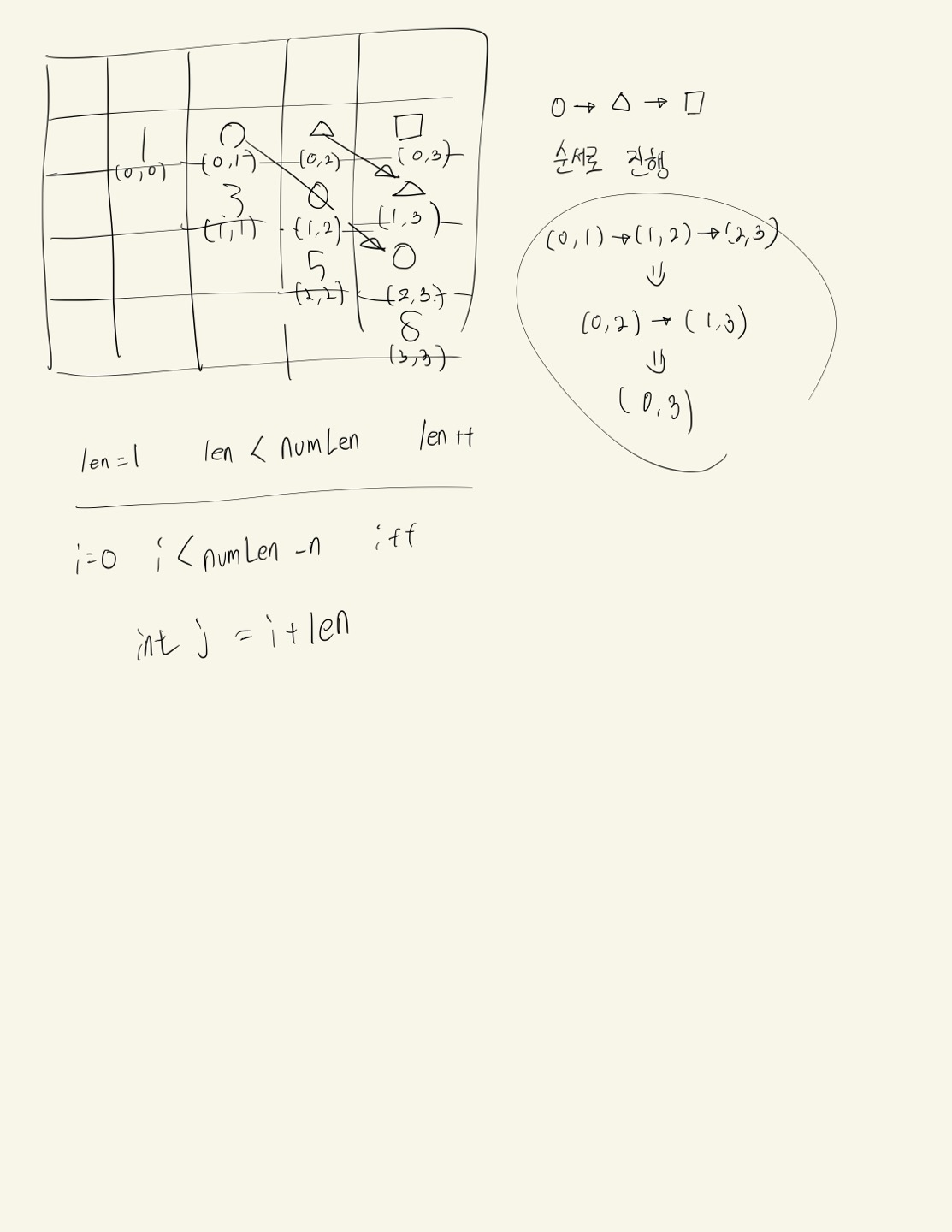
(0,0) , (1,1) ... (n-1,n-1)에는 숫자들이 들어간다. // n -> maxDP.length
이 후 (0,1) , (1,2) ... 순서로 maxDP에는 Integer.MIN_VALUE , minDP에는 Integer.MAX_VALUE 로 초기화한다.
그리고, 각 칸마다 자신 기준 왼쪽과 아래 칸을 기호에 맞게 연산하여 각각의 값을 채워넣는다.
(이 부분은 이해는 했으나, 말로 설명하기 어려운 것 같다.)

최종 결과는 maxDP[0][n-1] 이 최댓값이 나온다.

import java.util.*;

class Solution {
    public int solution(String[] arr) {
        int n = arr.length / 2 + 1; // 숫자의 개수
        int[][] maxDP = new int[n][n];
        int[][] minDP = new int[n][n];

        // 숫자 배열 초기화
        for (int i = 0; i < n; i++) {
            maxDP[i][i] = Integer.parseInt(arr[i * 2]);
            minDP[i][i] = Integer.parseInt(arr[i * 2]);
        }

        // DP 테이블 채우기 (길이 2 이상인 구간)
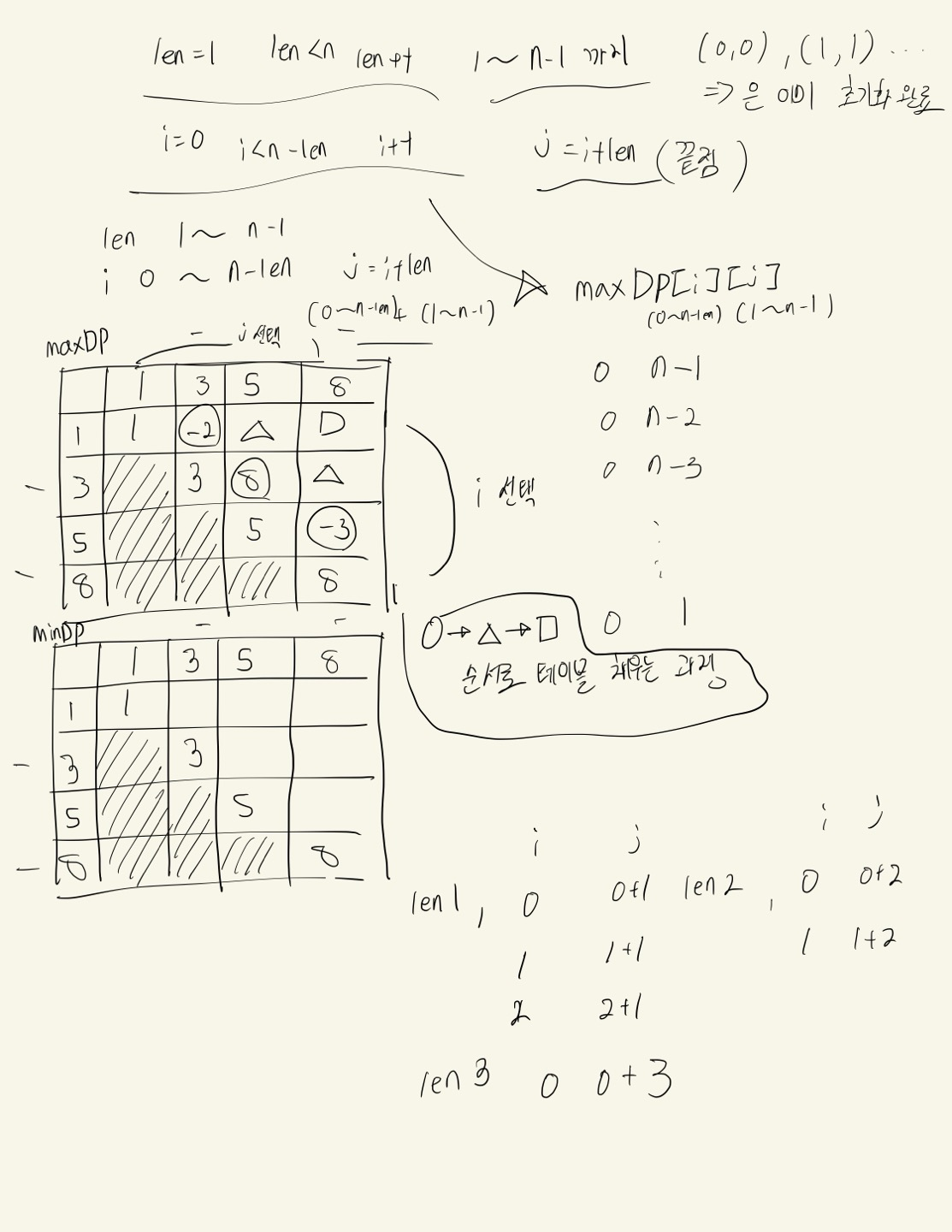
        for (int len = 1; len < n; len++) { // 길이: 2 ~ n까지
            for (int i = 0; i < n - len; i++) {
                int j = i + len;
                maxDP[i][j] = Integer.MIN_VALUE;
                minDP[i][j] = Integer.MAX_VALUE;

                // i부터 j까지 탐색하면서 k를 기준으로 분할
                for (int k = i; k < j; k++) {
                    String op = arr[k * 2 + 1]; // 연산자
                    if (op.equals("+")) {
                        maxDP[i][j] = Math.max(maxDP[i][j], maxDP[i][k] + maxDP[k+1][j]);
                        minDP[i][j] = Math.min(minDP[i][j], minDP[i][k] + minDP[k+1][j]);
                    } else { // "-"
                        maxDP[i][j] = Math.max(maxDP[i][j], maxDP[i][k] - minDP[k+1][j]);
                        minDP[i][j] = Math.min(minDP[i][j], minDP[i][k] - maxDP[k+1][j]);
                    }
                }
            }
        }

        return maxDP[0][n - 1]; // 전체 구간의 최댓값 반환
    }
}

출처
GPT

class Solution {
    int[][] maxDP;
    int[][] minDP;

    public int solution(String arr[]) {
        int numLen = arr.length / 2 + 1;
        maxDP = new int[numLen][numLen];
        minDP = new int[numLen][numLen];

        for (int i = 0; i < numLen; i++) {
            maxDP[i][i] = Integer.parseInt(arr[i * 2]);
            minDP[i][i] = Integer.parseInt(arr[i * 2]);
        }

        for (int len = 1; len < numLen; len++) {
            for (int i = 0; i < numLen - len; i++) {
                int j = i + len;
                maxDP[i][j] = Integer.MIN_VALUE;
                minDP[i][j] = Integer.MAX_VALUE;

                for (int k = i; k < j; k++) {
                    String op = arr[k * 2 + 1];

                    if (op.equals("+")) {
                        maxDP[i][j] = Math.max(maxDP[i][j], maxDP[i][k] + maxDP[k + 1][j]);
                        minDP[i][j] = Math.min(minDP[i][j], minDP[i][k] + minDP[k + 1][j]);
                    } else { // "-"
                        maxDP[i][j] = Math.max(maxDP[i][j], maxDP[i][k] - minDP[k + 1][j]);
                        minDP[i][j] = Math.min(minDP[i][j], minDP[i][k] - maxDP[k + 1][j]);
                    }
                }
            }
        }

        return maxDP[0][numLen - 1];
    }
}