문제 출처
코딩테스트 연습 > 탐욕법(Greedy) > 섬 연결하기
https://school.programmers.co.kr/learn/courses/30/lessons/42861
문제 설명
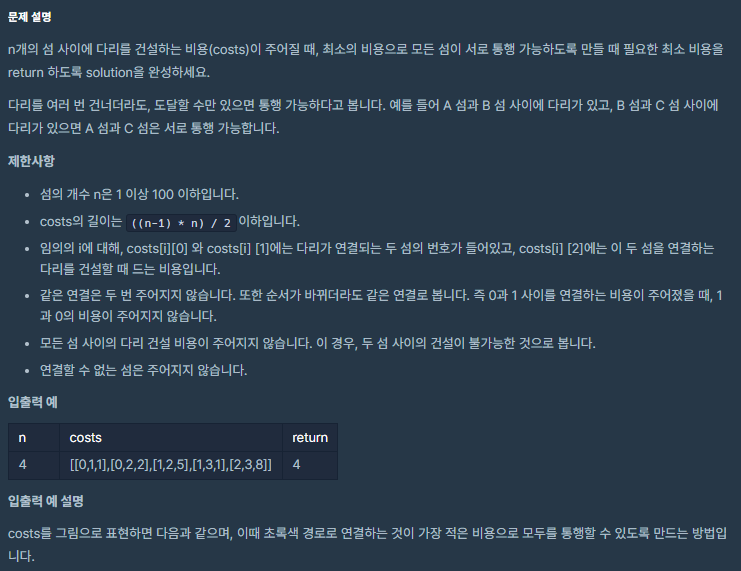
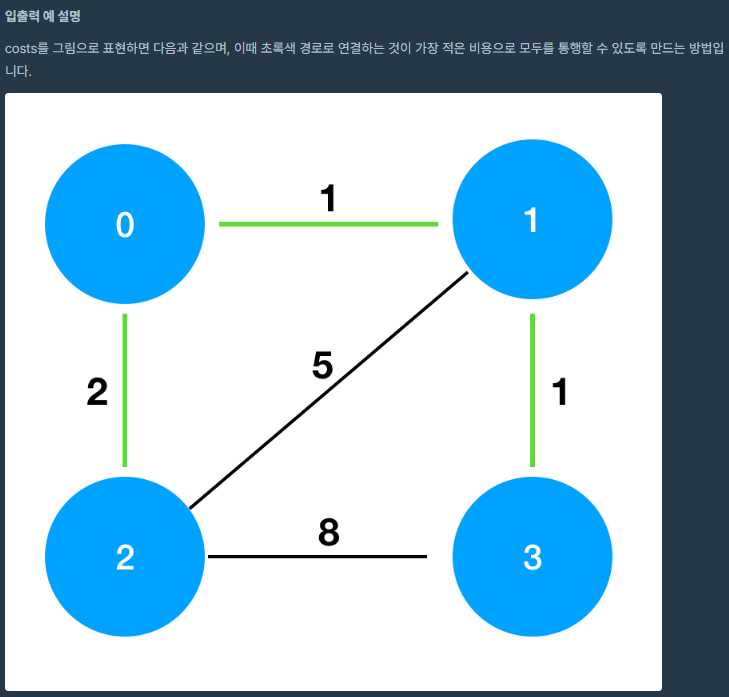
섬의 갯수 n, 각 섬마다 이어지는 다리 정보 및 다리 건설 비용 costs가 있을 때, 모든 섬이 통행 가능하도록 필요한 최소 비용을 return하라.
접근 방법
문제에서 가장 어려운 부분이자, 중요하게 해결해야하는 부분은
"만약 A,B가 연결되어있고, B,C가 연결되어있을 때, A,C는 연결되어있다." 라는 부분이 이 문제의 핵심이다.
이를 위해선 MST를 계산하는 Kruskal Algorithm을 이용해야한다.
parent 배열은 해당 다리가 어디에 연결되어있는지에 대한 정보이다.
이는 find 함수를 통해 root를 찾을 수 있다. 또한, union을 통해 두 다리를 연결한다.
costs 배열을 순회하며 costs[i][0] 과 costs[i][1]의 연결 정보를 바탕으로 union함수를 통해 다리를 합치고, 그에 대한 비용을 answer에 계속 더한다.
Kruskal
import java.util.*;
class Solution {
private int[] parent;
public int find(int a){
if(parent[a] == a) return a;
else return parent[a] = find(parent[a]);
}
public void union(int a, int b){
a = find(a);
b = find(b);
if(a != b){
parent[b] = a;
}
}
public int solution(int n, int[][] costs) {
int answer = 0;
parent = new int[n];
Arrays.sort(costs, (o1, o2) -> o1[2] - o2[2]);
for(int i =0; i<n; i++){
parent[i] = i;
}
for(int i = 0; i< costs.length; i++){
if(find(costs[i][0]) != find(costs[i][1])){
union(costs[i][0], costs[i][1]);
answer += costs[i][2];
}
}
return answer;
}
}Prim
Prim을 이용한 풀이는 노드마다 어디와 연결되어있는지에 대한 개별 노드 정보 Point를 모아둔 List를 이용하여 풀이한다.
하나의 노드는 여러가지 노드들과 연결되므로 각 개별 노드 정보 Point를 노드마다의 List를 저장하고 그 List를 저장하는 더 큰 List를 만들어서 저장한다.
해당 List에서 시작 노드를 꺼내서 노드 정보를 바탕으로 이어진 노드들을 탐색하여 이를 처리할 우선순위 큐(비용 기준 정렬)에 넣는다. 반복문을 이용하여 해당 과정을 반복하고, 이미 방문한 노드는 visited[노드] = true로 변경하여 더 이상 방문하지 못하게 한다.(우선순위 큐가 필요한 이유).
우선순위 큐가 비어질 때까지 반복한다.
import java.util.*;
class Solution {
public class Point implements Comparable<Point>{
int node, cost;
public Point(int node, int costs){
this.node = node;
this.cost = costs;
}
@Override
public int compareTo(Point o){
return this.cost - o.cost;
}
}
public List<List<Point>> map = new ArrayList<>();
public int solution(int n, int[][] costs) {
int answer = 0;
for(int i = 0; i< n; i++){
map.add(new ArrayList<>());
}
for(int i = 0; i <costs.length; i++){
int from = costs[i][0];
int to = costs[i][1];
int val = costs[i][2];
map.get(from).add(new Point(to, val));
map.get(to).add(new Point(from, val));
}
boolean[] visited = new boolean[n];
PriorityQueue<Point> queue = new PriorityQueue<>();
queue.add(new Point(0,0));
while(!queue.isEmpty()){
Point cur = queue.poll();
if(visited[cur.node]) continue;
visited[cur.node] = true;
answer += cur.cost;
for(int i = 0; i<map.get(cur.node).size(); i++){
int next = map.get(cur.node).get(i).node;
int cost = map.get(cur.node).get(i).cost;
if(visited[next]) continue;
queue.add(new Point(next, cost));
}
}
return answer;
}
}Review(kruskal)
import java.util.*;
class Solution {
static int path[];
// 두 다리가 연결되지 않은 경우 연결
public void union(int a, int b){
a = find(a);
b = find(b);
if(a != b) path[b] = a;
}
// 다리의 연결 정보 확인
public int find(int k){
if(path[k] == k) return k;
else{
return path[k] = find(path[k]);
}
}
public int solution(int n, int[][] costs) {
int answer = 0;
path = new int[n];
// 최소 비용 보장을 위한 정렬
Arrays.sort(costs, (o1,o2) -> o1[2] - o2[2]);
// 다리 연결 정보 초기화
for(int i = 0; i<n; i++){
path[i] = i;
}
// 다리를 모두 연결
for(int i=0 ; i<costs.length; i++){
if(find(costs[i][0]) != find(costs[i][1])){
union(costs[i][0],costs[i][1]);
answer += costs[i][2];
}
}
return answer;
}
}알게된 점
Union-Find를 이용하는 Kruskal 알고리즘에 대해서 알았다. 처음에 풀이할 때는, 그리디는 문제는 최적해를 구하는 것이니 각 다리의 연결 정보에서 가장 적은 비용을 갖는 다리만 남겨두고 이를 더해 계산한다는 방식으로 접근했으나, 이는 완벽한 오답이였다.
import java.util.*;
class Solution {
public int solution(int n, int[][] costs) {
int answer = 0;
int arr[][] = new int[n][n];
for(int i = 0; i<n; i++){
arr[costs[i][0]][costs[i][1]] = costs[i][2];
arr[costs[i][1]][costs[i][0]] = costs[i][2];
}
// 인접 행렬 생성
for(int i = 0; i<n; i++){
int min = ((n-1) * n) / 2 + 1;
for(int j = 0; j<n; j++){
if(arr[i][j] == 0) continue;
if(min > arr[i][j]){
min = arr[i][j];
}else{
arr[i][j] = 0;
}
}
// 다리가 중복되는 경우를 제외
} // arr에서 각 다리별 가장 낮은 cost 제외하고, 전부 0으로 바꿈
for(int k =0; k<n; k++){
for(int l = 0; l<n; l++){
if(arr[k][l] != 0){
answer += arr[k][l];
arr[l][k] = 0;
}
}
}
// arr에서 0이 아닌 수 answer++;
return answer;
}
}추가로 Prim 알고리즘 풀이도 공부해봤다.
전체적으로 BFS와 작동 방식이 유사하다고 생각하면 편하다.
단, 최소의 비용을 구해야하므로 우선순위큐를 통해 더 값이 비싼 다리가 오는 것을 배제한다.
문제푼 흔적
Kruskal


Review(kruskal)

