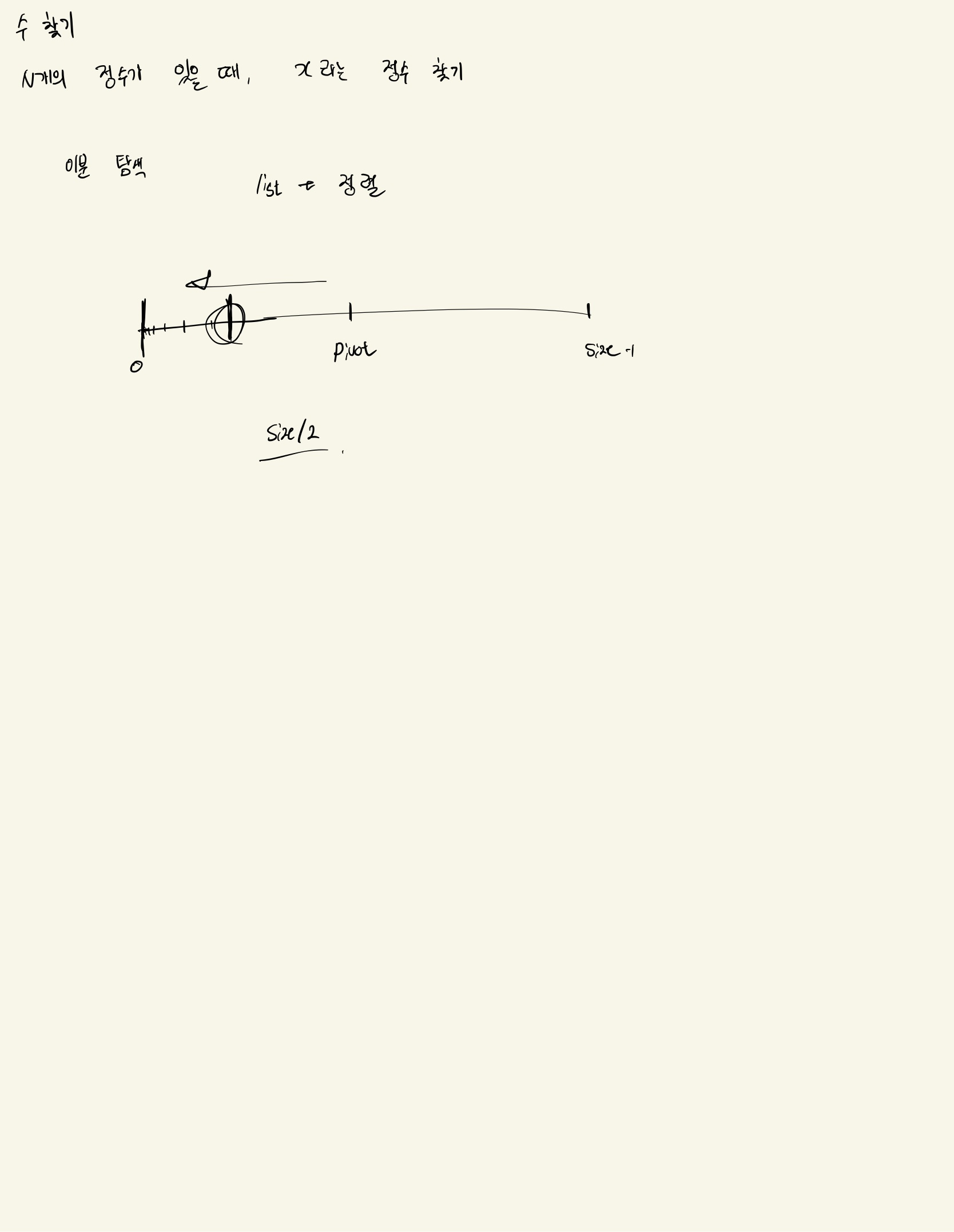
문제 출처

단계별로 풀어보기 > 이분 탐색 > 수 찾기
https://www.acmicpc.net/problem/1920

문제 설명

N개의 정수가 주어질 때, X라는 정수가 존재하는지 알아내라.

접근 방법

이분 탐색을 이용하여 풀이한다.
list의 size-1인 end, 처음 시작 인덱스인 0을 start 기준으로 이분 탐색을 진행한다.

import java.io.*;
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
import java.util.StringTokenizer;

public class 수_찾기 {

    public static List<Integer> list = new ArrayList<>();

    public static int binarySearch(int target, int start, int end){
        while(start <= end){
            int pivot = (start + end)/2;
            if(list.get(pivot) > target){
                end = pivot-1;
            } else if(list.get(pivot) < target){
                start = pivot+1;
            } else{
                return 1;
            }
        }
        return 0;
    }

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

        int N = Integer.parseInt(br.readLine());

        StringTokenizer st = new StringTokenizer(br.readLine());

        for(int i = 0; i < N; i++){
            list.add(Integer.parseInt(st.nextToken()));
        }
        Collections.sort(list);

        int M = Integer.parseInt(br.readLine());
        st = new StringTokenizer(br.readLine());

        StringBuilder sb = new StringBuilder();

        for(int i = 0; i < M; i++){
            int target = Integer.parseInt(st.nextToken());
            int start = 0;
            int end = list.size()-1;

            sb.append(binarySearch(target, start, end)).append("\n");

        }

        bw.write(sb.toString());
        bw.flush();
        bw.close();
        br.close();

    }
}

알게된 점

이분 탐색의 시간 복잡도는 O(log N)이다. 코드에서는 M개를 찾기 위해서 M번 돌렸으므로, O(M log N)이 되는데, 여기서 이분 탐색을 위해 정렬까지 진행했으므로 O((M + N) log N)이 나오게 된다.

문제푼 흔적