문제 출처

단계별로 풀어보기 > 그리디 알고리즘 > 잃어버린 괄호
https://www.acmicpc.net/problem/1541

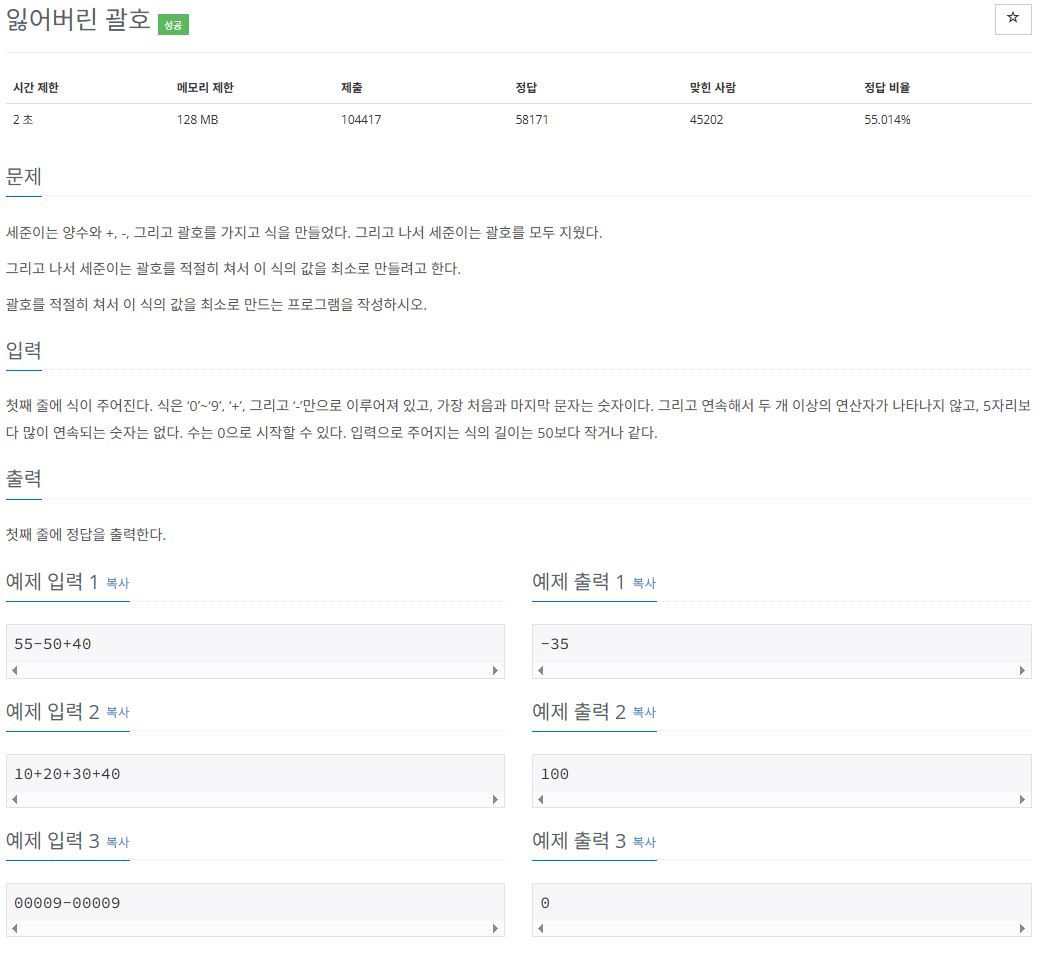
문제 설명

식(문자열)이 주어질 때, 해당 식에 괄호를 이용하여 식의 최솟값을 return 하라.

접근 방법

식에 "+","-", 양수 만 있을 때, 최솟값이 나오는 기준을 알아야한다.
해당 경우에는 "-" 기호 뒤에 있는 식을 모두 큰 수로 만들어 주면 된다.
예시로 55 - 50 + 40 은 "-" 기호 뒤에 있는 50 과 40을 더하여 55 - (50 + 40)의 형태로 변경한다.
이를 위해 문자열을 "-" 기준으로 split하고, 해당 split한 것을 저장한 배열을 순회하며 다시 "+" 으로 split한다. 이 때, "+" 기준으로 split한 것은 더한 후, 최종 결과에서 빼준다.

import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.ArrayList;

public class 잃어버린_괄호 {
    public static void main(String[] args) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

        String exp = br.readLine();

        String[] minusSplit =exp.split("-");

        int result = 0;

        for(int i = 0; i<minusSplit.length; i++){
            String[] plusSplit = minusSplit[i].split("\\+");

            int sum = 0;

            for(String num : plusSplit){
                sum += Integer.parseInt(num);
            }

            if(i == 0){
                result += sum;
            } else{
                result -= sum;
            }
        }

        bw.write(String.valueOf(result));
        bw.flush();
        bw.close();
        br.close();
    }
}

Review

import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;

public class 잃어버린_괄호_review {
    public static void main(String[] args) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

        String[] minusSplit = br.readLine().split("-");

        int result = 0;

        for(int i = 0; i< minusSplit.length; i++){
            String[] plusSplit = minusSplit[i].split("\\+");
            int sum = 0;
            for(String num : plusSplit){
                sum += Integer.parseInt(num);
            }
            if(i == 0){
                result += sum;
            } else {
                result -= sum;
            }
        }

        bw.write(String.valueOf(result));
        bw.flush();
        bw.close();
        br.close();
    }
}

알게된 점

"+"의 경우 정규식을 작성할 때, 백슬래쉬를 붙혀줘야 인식이 되는데, 이 때, "\"도 혼자서 인식이 안되므로 2개를 사용한다.
Review
주의 해야할 점으로 result == 0 일 때, result += sum을 실행하는 것으로 짰었는데, 이는 맨 앞 수가 0이 올 경우에는 로직이 성립하지 않는다.

문제푼 흔적