문제 출처

단계별로 풀어보기 > 분할 정복 > 종이의 개수
https://www.acmicpc.net/problem/1780

문제 설명

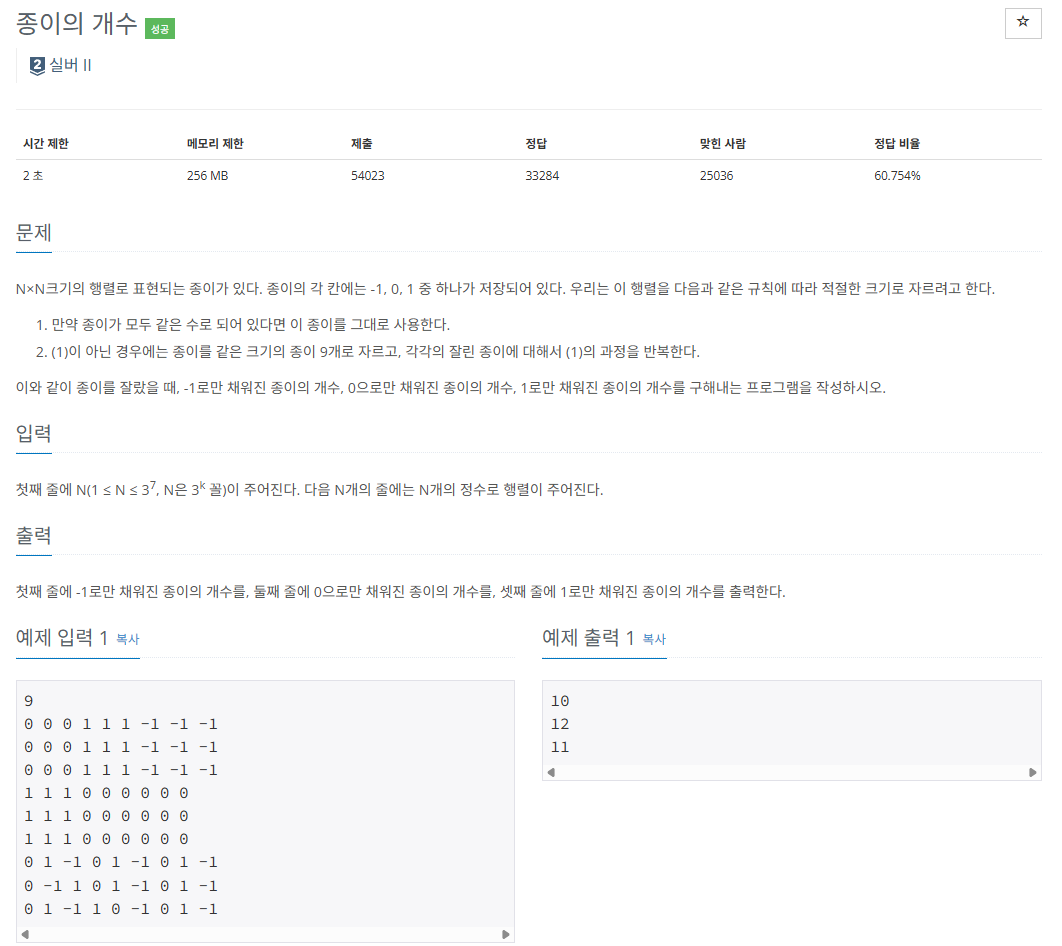
N x N 크기의 행렬로 표현되는 종이 각 칸에는 -1,0,1 중 하나가 저장되어ㅣㅆ다.
해당 행렬을 다음과 같은 규칙으로 적절한 크기로 자르려고 한다.
(1) 만약 종이가 모두 같은 수로 되어 있다면 이 종이를 그대로 사용한다.
(2) (1)이 아닌 경우에는 종이를 같은 크기의 종이 9개로 자르고, 각각의 잘린 종이에 대해서 (1)의 과정을 반복한다.
해당 과정을 반복한 후, -1,0,1로 채워진 종이의 개수를 순서대로 출력하라.

접근 방법

한 범위에 대해서 같은 숫자로 이루워져 있는지 확인하는 isPossible를 이용하여 검사한다.
이 후, 전체가 같은 숫자라면 숫자에 해당하는 변수를 1 증가시키고, countPaper를 return 한다. 만약 같지 않다면, 처음 size / 3 의 크기에 해당하는 newSize를 바탕으로 9개의 범위를 재귀를 이용하여 검증한다.

import java.io.*;
import java.util.StringTokenizer;

public class 종이의_개수 {
    public static int[][] arr;
    static int minus = 0;
    static int zero = 0;
    static int plus = 0;

    public static boolean isPossible(int x, int y, int size){
        int recent = arr[x][y];
        for(int i = x; i < x + size; i++){
            for(int j = y; j < y + size; j++){
                if(recent != arr[i][j]) return false;
            }
        }
        return true;
    }

    public static void countPaper(int x, int y, int size){
        if(isPossible(x,y,size)){
            if(arr[x][y] == -1) minus++;
            if(arr[x][y] == 0) zero++;
            if(arr[x][y] == 1) plus++;
            return;
        }

        int newSize = size / 3;
        countPaper(x,y,newSize);
        countPaper(x,y+newSize,newSize);
        countPaper(x,y+newSize+newSize,newSize);
        countPaper(x+newSize,y,newSize);
        countPaper(x+newSize,y+newSize,newSize);
        countPaper(x+newSize,y+newSize+newSize,newSize);
        countPaper(x+newSize+newSize,y,newSize);
        countPaper(x+newSize+newSize,y+newSize,newSize);
        countPaper(x+newSize+newSize,y+newSize+newSize,newSize);

    }
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

        int N = Integer.parseInt(br.readLine());

        arr = new int[N][N];

        StringTokenizer st;
        for(int i = 0; i < N; i++){
            st = new StringTokenizer(br.readLine());
            for(int j = 0; j < N; j++){
                arr[i][j] = Integer.parseInt(st.nextToken());
            }
        }

        int size = arr.length;

        countPaper(0,0,size);

        StringBuilder sb = new StringBuilder();
        sb.append(minus).append("\n").append(zero).append("\n").append(plus);
        bw.write(sb.toString());
        bw.flush();
        bw.close();
        br.close();
    }
}

알게된 점

해당 코드의 시간 복잡도는 N x N 범위를 전체를 확인하고, 만약 같지 않다면 size / 3 을 진행한 범위를 계속 탐색해야한다. 따라서 시간 복잡도는 O(N^2 logN)이다.

문제푼 흔적