결론: 비트를 향해 가는 여정
이 책의 앞선 챕터들에서는 모스부호, 전구의 작동방식, 십진수 등에 대해서 알아봤습니다.
바로 앞 챕터에서는 십진수가 얼마나 유용한지, 역사적인 의의는 어떤 것이 있는 지 등에 대해 알아봤습니다. 이번 챕터에서는 십진수 외에 8진수와 2진수에 대해 서술하고 있습니다.
인간에게 손(발)가락이 네 개였다면?!
본문에서는 앞선 챕터에서도 언급했듯이 10진수가 보편화 된 이유는 인간의 손가락이 한 손에 5개에서 기인한 것이라고 말하고 있습니다. 10이 반드시 "10개"라는 개수를 가르킬 필요는 없습니다. 책의 예로는
책에서는 오리로 나와있지만 이 두 개의 사과를 2진수로 표현했을 때
2진수란 1과 0 두 개의 숫자만으로 표현되기 때문에 2라는 표기가 없이 10으로 표기하는 것을 이해하는 것이 이 챕터가 궁극적으로 도달 하고자 하는 목표입니다.
이것을 이해하기 위해 우선 거쳐가는 단계가 8진수 입니다. 앞서 언급한 2진수에서 2가 없는 것과 마찬가지로 8진수 역시 8이 없습니다. 8진수에서 여덟개를 나타내는 기호는 10이지요.
96페이지에 나와있는 그림을 참조하면 이해가 더 쉬울 것 같습니다.
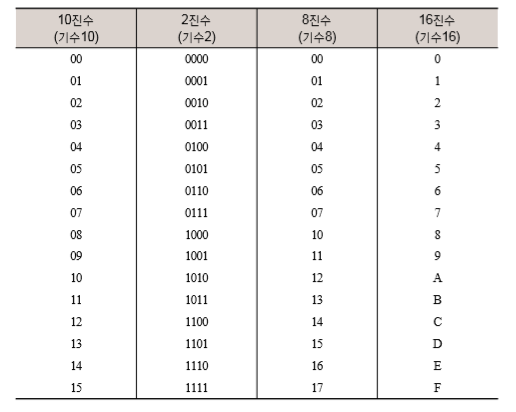
8진수를 이해하기 위해 위의 표를 첨부합니다. 그리고 본문의 98페이지에서는 2의 거듭제곱도 함께 표기되어있습니다. 이것은 이진수를 이용하는데 있어 십진수가 아닌 팔진수를 이용하는 것이 더 유용할 수 있다는 점을 눈에 띄게 보여주는 표기입니다.
8진수의 표기
링크텍스트
팔진수 역시 10진수와 같이 자리수에 따라 분리 해서 볼 수 있습니다. 마찬가지로 덧셈표도(100페이지) 곱셈표도(101페이지) 나타낼 수 있습니다.
2진수
랍스터를 집게발을 인용한 4진수에 대한 간략한 설명을 지나 드디어 돌고래 물갈퀴를 이용한 2진수에 도달했습니다. 2진수는 처음 사과에서 언급한 것과 같이 1과 0으로만 구성 된 숫자 개념입니다.
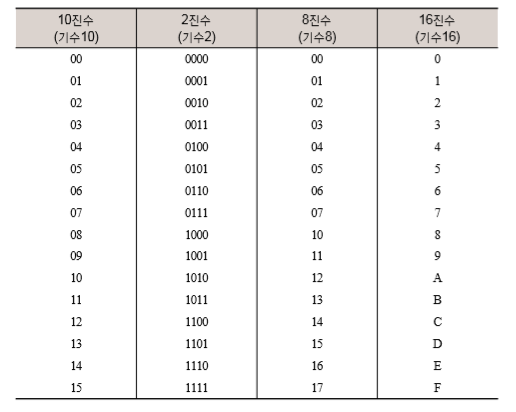
위 표에서 한번더 2진수의 표기 방법을 알 수 있습니다.
우리가 익숙한 자릿수에 의한 표기법은 다음과 같습니다.
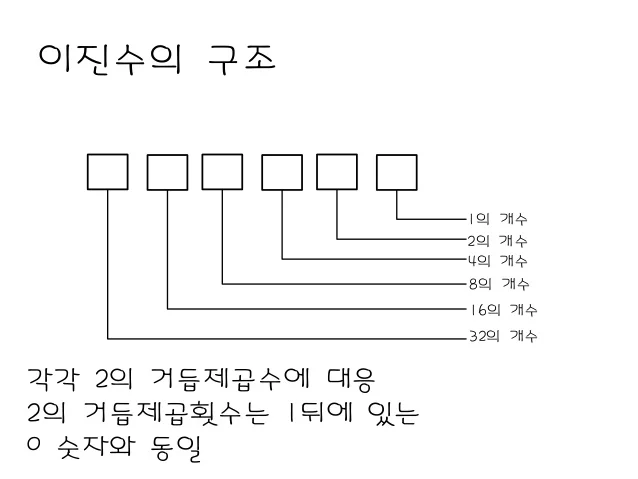
링크텍스트
10진수에서 2진수로 변환하는 것은 아래와 같습니다.
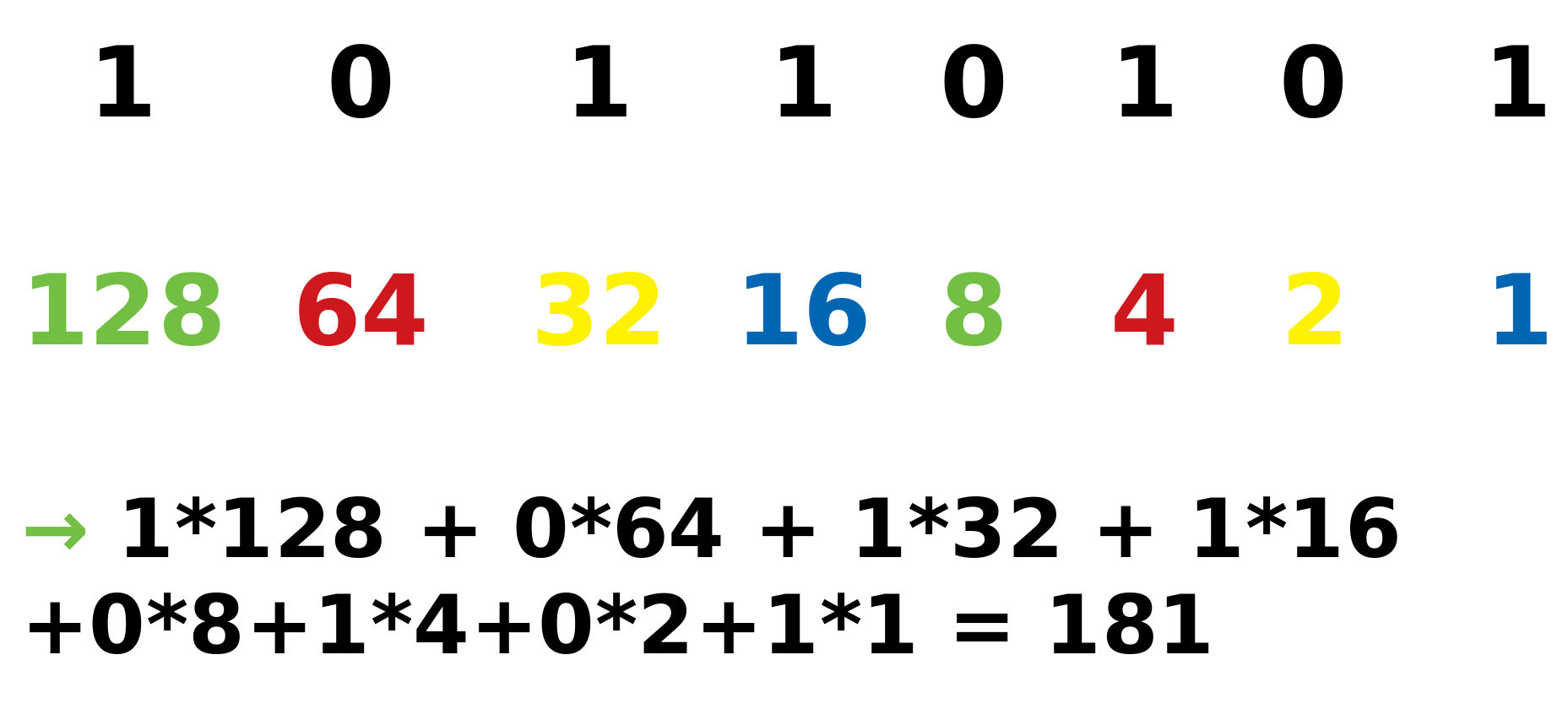
링크텍스트
2진수의 덧셈과 곱셉을 보면(각각 페이지 108과 109) 10진수나 8진수에 비해서 훨씬 간단하다는 사실을 알 수 있습니다.
*컴퓨터 언어에서 2진수를 사용하는 이유 중 하나가 이러한 간단한 연산에 있다고도 합니다.
링크텍스트
2진수는 연산이 간단하지만 대신 두 숫자 밖에 없기 때문에 다른 진수들에 비해 쉽게 길어집니다. 예를 들어 2진수를 이용해 천이백만을 이진수로 나타낼 경우 '101101110001101100000000'이 됩니다. 따라서 2진수를 표기할 때는 가독성을 높이기 위해 네자리마다 '-'나 ' '를 추가해 '1011-0111-001-1011-0000-0000' 등으로 표기하는 형식이 일반적입니다.
드디어 앞서 나온 전선, 전구와의 관계성
멀고멀리 돌아와 드디어 친구와의 통신을 위한 전구와 전선, 스위치 등으로 돌아왔습니다. 2진수는 앞서 전구, 전선, 스위치를 표현할 수 있습니다. 전류가 흐를 때: 1, 흐르지 않을 때: 0 으로 아주 간단하면서 효과적으로 표기할 수 있습니다. 전선이 릴레이로 연결되어 있을 때도 마찬가지로 표현할 수 있습니다.
링크텍스트
1938년경 미국의 수학자 존 와일더 터키(위키피디아에는 존 튜키로 표기)는 컴퓨터가 유행 됐을 때 이진수가 더 중요한 의미를 가지리라는 것을 알았습니다. 그래서 그는 이진수(Decimal)이란 말 대신 더 짧은 bit라는 단어를 사용하기로 결정했습니다.
*이 존 튜키가 소프트웨어라는 말도 처음 사용 했다고 하네요
- 3줄요약
- 2진수를 이해하기 위한 8진수의 이해
- 2진수의 표기 방법
- 2진수를 통한 전선/전구/전류의 표현
추가 내용: ASCII(아스키)는 문자를 컴퓨터가 이해할 수 있는 이진 데이터(0 또는 1)로, 혹은 그 반대로 변환하는 표준 방법이다.
2진수와 컴퓨터 추가 내용 링크텍스트
