용어정리
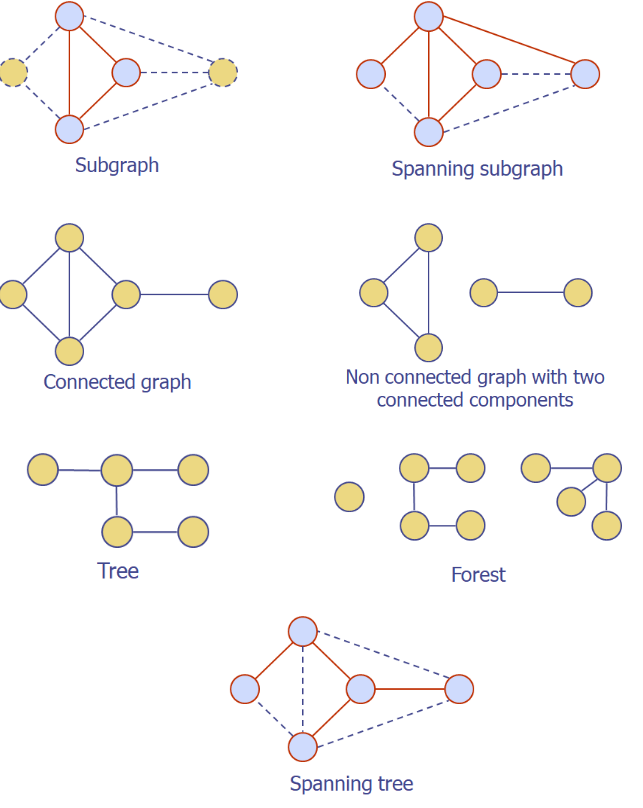
Subgraph (부분 그래프)
- 그래프 G(V, E) 에 대해 S(V', E') 가 그래프이면서 V' ⊂ V 와 E' ⊂ E 를
만족할 때, S 를 G 의 부분 그래프라고 한다.
Spanning subgraph (신장 그래프)
- subgraph 중 기존 그래프 G의 모든 정점을 포함하는 그래프
=> V' = V
(단, 기존 그래프 G의 모든 정점을 가지되, 모든 간선을 가지진 않고 일부분만 포함)
Connected graph
- 모든 정점이 간선으로 연결되어있는 그래프
즉, 모든 간선의 양 끝이 정점과 연결되어있고, 간선과 연결되지 않은 정점은 없다.
Connected component
- connected subgraph 중 가장 큰 그래프
Tree
- 연결그래프이면서 사이클이 없는 그래프
- 트리에서 임의의 두 정점 사이의 path 는 반드시 1개이다.
cf. 이전에 배운 트리를 rooted tree 라고 부른다.
Forest
- 트리들의 집합. 즉, 트리가 Connected component 으로써 모여있는 것
Spanning Tree
-
spanning subgraph 가 트리인 그래프.
연결 그래프의 spanning subgraph 가 tree 조건을 만족하면 Spanning Tree 라고한다. -
즉, 사이클이 없으며 연결 그래프이고 기존 그래프 G의 모든 정점을 포함하는 그래프이다.
-
다시말해, 원래 그래프 G가 트리가 아니라면 spanning tree 는 유일하지 않을 수 있다.
Spanning forest
- spanning tree 의 집합체
DFS
- 더 깊이 들어갈 수 없을때까지 탐색하는 알고리즘
- 다음 분기로 넘어가기 전에 해당 분기를 완벽하게 탐색하고 넘어간다.
- 재귀함수를 이용하기 때문에 한번 방문한곳인지 검사하지 않으면 무한루프에 빠질 수 있다.


수도코드
- label
- 종류 : UNEXPLORED, VISITED, DISCOVERY, BACK
- 이미 방문한 정점 or 간선인지 아닌지를 상태를 상수로 저장하는 변수
- vertex, edge 객체에 label 필드를 추가해서 상태를 저장
- setLabel, getLabel 메소드를 통해 label 에 접근할 수 있다.
- edge의 label 종류
- UNEXPLORED : 아직 확인 안해본 간선임을 의미
- DISCOVERY : 새로운 정점을 향해서 가게된 길(간선)임을 의미
- BACK : 아까 방문했던 지점(정점) 을 향해가는 edge 임을 의미
- 즉, 아까 방문했던 정점이라서 가면안되고 기존 정점으로 다시 되돌아오게 된 길 (간선)임을 의미
- vertex의 label 종류
- UNEXPLORED
- VISITED
Algorithm DFS(G)
Input graph G
Output labeling of the edges of G
as discovery edges and back edges
for all u ∈ G.vertices() // 모든 정점과 간선의 label를 UNEXPLORED로 초기화 => 각각 엣지시퀀스와 정점시퀀스 따라가면서 모든 엣지 및 정점 오브젝트의 label 필드를 0으로 초기화하는 작업 : O(n) / O(m)
u.setLabel(UNEXPLORED)
for all e ∈ G.edges()
e.setLabel(UNEXPLORED)
for all v ∈ G.vertices() // 모든 정점에 대해 탐색
if v.getLabel() = UNEXPLORED // 아직 방문안한 정점이면
DFS(G, v) // DFS 탐색실행Algorithm DFS(G, v) // 현재 보고있는정점 : v
Input graph G and a start verrtex v of G
Output labeling of the edges of G
in the connected component of v
as discovery edges and back edges
v.setLabel(VISITED) // 현재 정점을 방문처리 : O(1)
for all e ∈ G.incidentEdges(v) // 현재 정점과 인접한 모든 간선중에 아직 확인 안해본 간선들에 대해 탐색
if e.getLabel() = UNEXPLORED // 한번도 아직 확인안해본 간선이라면 => 색깔 확인하는데 O(1)
w = e.opposite(v)
if w.getLabel() = UNEXPLORED // 해당 간선이 가리키고 있는 반대편 정점을 확인해보니, 이 정점이 아직 방문 안한 곳이라면
e.setLabel(DISCOVERY) // 정점을 향해 가본 간선임을 표시. 단, 왔던 길을 다시 돌아가면 안된다는 뜻도 포함되어있다!
DFS(G, w) // 함수 호출하는데 O(1)
else // 이 정점이 아까 방문 했던 곳이라면
e.setLabel(BACK) // 간선이 아까 방문했던 정점을 향해가는 간선이라고 표시 => O(1)DFS 수행시간
- incidentEdges() 의 시간에 따라서 DFS 수행시간이 결정된다!
(다른 작업은 모두 O(1)이기 때문)
=> 인접리스트로 구현했다면 O(deg(v) + 1) 이다.
1) O(deg(v))
- 해당 정점의 incidence 시퀀스를 가서 엣지 오브젝트 찾는데 O(1)
- 결국 엣지 개수(= 해당 정정의 incidence 시퀀스 원소개수) 만큼 반복
2) O(1)
- 해당 정점도 처리해줘야 하므로
예시
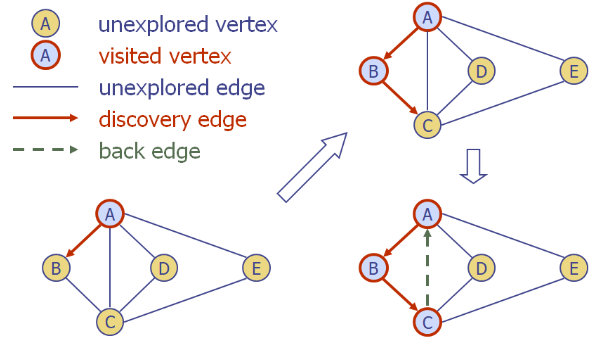
여러개의 vertex 로 뻗어나가서 탐색을 진행할 수 있을떄, 알파벳 순으로 탐색을 진행한다고 가정하자.
과정1
-
DFS(G) 로 모든 정점과 간선을 UNEXPLORED 를 초기화한다.
-
이후 DFS(G, A) 를 호출
-
A와 인접한 간선들을 조사한다 (간선 AB, AB, AD, AE 순으로)
-
간선 AB가 UNEXPLORED이므로 B 가 UNEXPLORED 인지 조사한다.
-
B가 UNEXPLORED 이므로 간선 AB 를 EXPLORED 로 바꾸고 DFS(G, B) 를 호출한다.
-
B를 VISITED 표시한다.
-
B와 인접한 간선을 조사한다. ( 간선 BA, BC 순으로 )
-
간선 BA가 UNEXPLORED가 아니므로 BACK 표시하고 간선 BC 를 조사한다.
-
간선 BC 가 UNEXPLORED 이고 C 도 UNEXPLORED 이므로 DFS(G, B) 를 실행한다.
-
이런식으로 계속 진행됨!
cf. ABCDE 와 연결되지 않은 connectes component 인 FG가 있을때 한번 DFS(F)로 옮겨온다음 여기도 마찬가지로 방문함!
과정2
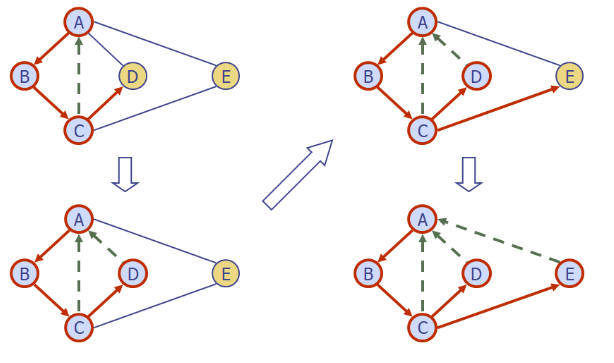
DFS 탐색결과 분석
-
DFS(G, v) 는 v 와 연결된 conntected component 를 방문한다
-
DFS(G, v) 의 결과에서 DISCOVERY 간선으로 연결된 그래프는
v와 연결된 conntected component 의 spanning tree 이다.
(cf. 모든 정점을 연결하면서 순회하지 않는 최대의 단위라는 뜻)
DFS를 인접리스트로 구현시 수행시간
DFS를 인접리스트로 구현했을때 수행시간이 O(n+m) 이 걸리는 이유는 아래와 같다.
-
모든 정점, 간선 label 초기화 => O(n+m)
-
Σv ( O(1) + O(deg(v)) ) = 2m = O(m)
실제 수행에도 모든 정점에 대해 O(1)+O(deg(v)) 시간이 걸림
-
2-1. 현재 탐색하는 정점의 incidence 시퀀스의 모든 엣지 오브젝트에 대해 방문처리(label 필드값 변경) => deg(v)
-
2-2. 해당 정점도 처리해야 하므로 => O(1)
=> 이 작업을, 즉 O(1) + O(deg(v)) 작업을 모든 정점에 대해서 수행한다.
- O(1) 작업을 모든 정점에 대해서 반복 => O(n)
- O(deg(v)) 작업도 모든 정점에 대해서 반복 => 2m = O(m)
- 모든 정점의 차수를 합한 값 = 2m 이므로!
따라서 O(n+m) + O(m) = O(n+m) 이다!