
컴퓨터의 연산처리
- 컴퓨터는 1초에 3~5억개의 연산을 처리 가능
=> 문제에서 제한시간이 1초이다?
이 말은 곧 "당신이 설계한 코드, 즉 프로그램은 3~5억번의 연산 안에 답을 도출해내고 종료되어야 한다." 라는 것이다.
그런데 이렇게 3~5억 번의 연산안에 설계해야 한다고만 하면 난해하다.
우리는 기준이 필요하다.
연산횟수
아래 코드의 연산 횟수를 분석해보자.
( n에 관한 함수로 표현해보자! )
int func1(int arr[], int n){
int cnt = 0;
for(int i = 0; i < n; i++){
if(arr[i] % 5 == 0)
cnt++;
}
return cnt;=> 정답 : 1 + 1 + n x ( 2 + 2 + 1 ) + 1 = 5n + 3
1 : cnt 변수를 선언하고 0을 할당
1 : for 문에서 변수 i 를 선언하고 초기값 0을 할당
=> 1+1 = 2
--
2 : i가 n보다 작은지 확인하고 + 작을 경우 1 증가시키기
2 : arr[i] 를 5로 나눈 나머지를 계산하고 + 그 값이 0과 일치하는지 확인
1 : 5의 배수라고 치면 cnt 를 1 증가시켜야 하니 연산 1번
=> n번 반복. 즉 5n
--
1 : 이후 마지막으로 cnt 를 반환할 때 연산 1번이 추가로 필요
=> 1
위 함수는 5n+3 번의 연산이 필요하다.
ex1) n = 100만일때 => 대략 500만번의 연산이 필요하니, 1초안에 충분히 통과 가능
ex2) n = 10억일때 => 개략 50억번의 연산이 필요하니, 1초안에 다 돌수가 없다.
Time Complexity => 노가다를 줄이자!
- 위와 같이 연산횟수(primitive operation) 의 횟수를 일일이 카운팅 하는 것은 하루종일 걸린다. (매우 비효율적)
귀찮은 노가다를 연신을 줄이기 위해, 우리는 "5n+3" 이라는 연산이 "n에 비례한다" 라고만 표현하자!
즉 상수를 제거하고, n에 관해서만 표현하자. => "시간 복잡도"
- n에 비례한다고 어떻게 빠르게 분석할 수 있는가?
int func1(int arr[], int n){
int cnt = 0;
for(int i = 0; i < n; i++){
if(arr[i] % 5 == 0)
cnt++;
}
return cnt;=> 위 코드는 for문에서 n개의 수를 훑어보며 5로 나눈 나머지를 게산하게 되는 것이라고 바로 알 수 있을 것이다.
요약 : 시간복잡도란 프로그램 코드의 연산 횟수를 간단히 n에 관해서 표현하는 기법이다.
예제 - Average Case / Worst Case / Best Case
문제1
문제)
대회장에 N명의 사람들이 일렬로 서있다. 거기서 당신은 "이민성" 인 사람을 찾기 위해 사람들에게 이름을 물어볼 것이다. 이름을 물어보고 대답을 듣는데까지 1초가 걸린다면 얼마만큼의 시간이 필요할까?
(조건 : 이때 사람들은 이름순으로 서있는게 아닌, 무작위로 배치 서있음)
정답)
앞에서부터 차례대로 물어보면 된다.
최악의 경우 : N초 ( ex. 사람의 수가 100명인 경우 : 100초)
최선의 경우 : 1초 ( ex. 사람의 수가 100명인 경우 : 1초)
평균적인 경우 : N/2 초 가 걸릴것이다. ( ex. 사람의 수가 50명인 경우 : 50초)
=> "걸리는 시간은 N에 비례한다"
문제2
문제)
대회장에 N명의 사람들이 일렬로 서있다. 거기서 당신은 "이민성" 인 사람을 찾기 위해 사람들에게 이름을 물어볼 것이다. 이름을 물어보고 대답을 듣는데까지 1초가 걸린다면 얼마만큼의 시간이 필요할까?
(조건 : 이때 사람들은 이름순으로 서있는게 아닌, 이때 사람들은 이름순으로 서있다. 즉, 가나다 한글순으로 배치되어 있다. )
정답)
업다운(UP-DOWN) 게임을 떠올리면 된다. 업다운 게임처럼 중간 사람이 "이민성" 인지 계속 물어보면 된다.
=> 즉, 100명의 사람이 있을떄 가운데 있는 사람의 이름을 물어봐서 50명을 남기고, 50명에서 또 가운데 있는 사람을 물어봐서 25명을 남기고, .... 이 과정을 반복한다.
- 최선의 경우 : "1초" 가 걸린다. 즉, 이민성이 정확히 한 가운데에 위치한 경우 1번만의 연산으로 바로 찾아낼 수 있다.
- 최악의 경우 : "logN 초"가 걸린다. 즉, 최악의 경우는 한명이 남을때까지 절반으로 계속 쪼개지는 상황이다. (ex. 사람의 수가 8명인 경우 : 3초 )
- 평균적인 경우 : "logN 초" 가 걸릴것이다. ( => 왜 logN 인지 이해안가면 그냥 넘기자)
시간복잡도(Time Complexity), 빅오표기법(Big-O Notation)
시간복잡도 : 입력의 크기와 문제를 해결하는데 걸리는 시간의 상관관계
=> 위 예제에서 살펴본 log N초, N초 등이 각 문제(프로그램 코드)의 시간복잡도 인것이다.
빅오표기법 : 주어진 식을 값이 가장 큰 대표항만 남겨서 나타내느 방법
- 빅세타, 빅오메카, 빅스몰세타, 빅스몰오메가 => 몰라도 된다!
예시
O(n) 으로 표현되는 식 예제 => 5n+3, 2n + logn, logn
O(n^2) 으로 표현되는 식 예제 => n^2+ 2n + 4, 6n^2 + 20n + 10logn
o(nlogn) 으로 표현되는 식 예제 => nlogn + 30n + 10, 5nlogn + 6
O(1) 으로 표현되는 식 예제 => 5, 16, 36 ex. O(n) = 5n+3
=> 누가봐도 n이 커지면 커질수록 3보다는 5n이 훨씬 크다.
3이라는 상수는 실행시간에 거의 절대로 영향력이 없다고 봐도 무방할 것이다.
즉, 실행시간 "5n+3" 은 상수 3에 의해 영향을 받지 않는다. n에 대해서만 영향을 받는다.
그런데 3을 일단 제외했을 떄 식에 5n 이 보일텐데, 숫자 5도 무시해도 무방하다.
n이 10억이 라면, n에 5가 곱해진다고 한들, 큰 영향을 미치지 않는다.
정리1 : 시간복잡도를 표현할 때 n에 관한 가장 큰 대표항만 남기자!
(저차항, 상수계수는 모조리 무시한다. 실행시간에 큰 영향을 미치지 않기 떄문이다.)
ex. 5*n^2 + 2n + 3 에서 저차항, 상수를 모두 제거하면 n^2 만 남게된다.
정리2 : 시간복잡도를 표현하는 방법 = 빅오표기법
(빅오표기법이란, n에 관한 함수를 저차항, 상수계수를 모두 제거하고 순수히 n에 관한 최고차항만 남기는 표기법이다.)ex1. 실행시간 5n+3 을 빅오표기법으로 표현시, O(n) 만큼 실행된다고 표현한다.
ex2. 실행시간 n^3 + 3n + 1 을 빅오표기법으로 표현시, O(n^3) 만큼 실행된다고 표현한다.
시간복잡도에 따른 수행시간
시간복잡도가 달라짐에 따라서 실행시간이 매우 크게 차이남을 볼 수 있다.
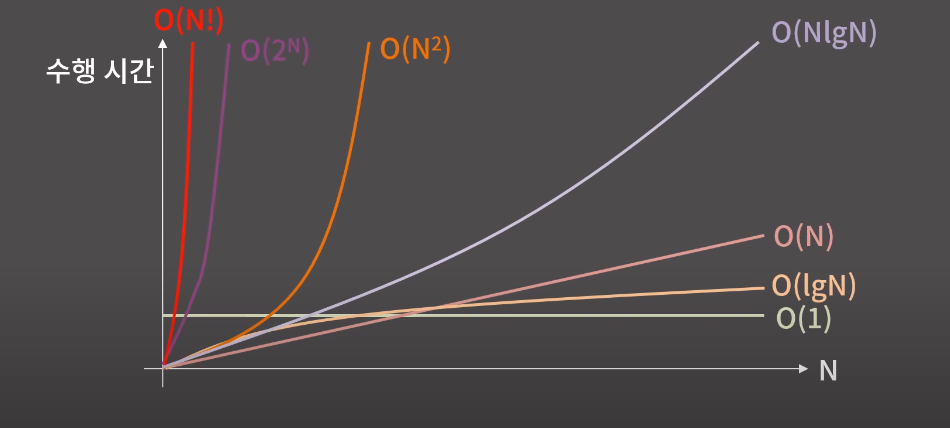
O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(2^n) < O(n!)
- 참고
O(n) : linear time
O(logn) : log time
그 이상 : 다항 시간
O(2^n) : n이 25이하 정도로 굉장히 작은것이 아니라면, O(2^n) 이 필요한 풀이는 런타임 에러가 뜰 가능성이 굉장히 높다.
문제의 시간제한을 보고 시간복잡도 얼추 설계하기
- 내 풀이가 제한시간안에 통과할 수 있을지 제발!! 설계를 잘 하고 풀자.
n의 크기 허용 시간복잡도
n <= 11 O(n!)
n <= 25 O(2^n)
n <= 100 O(n^4)
n <= 500 O(n^3)
n <= 3000 O(n^2logn)
n <= 5000 O(n^2)
n <= 1,000,000 O(n)
n <= 10,000,000 O(logn), O(1)공간복잡도
-
설계한 프로그램 코드가 공간을 얼마나 차지하는지 의미
ex. int형 배열을 이중 for문을 돌려서 생성했을때, 인풋의 크기가 n인 경우 공간복잡도는 O(n^2) 이 된다. -
메모리 제한이 512MB 일떄, 1.2억개 크기의 int형 배열을 선언할 수 있다는 것만 기억하자.
(int형 메모리 하나가 4바이트를 차지하는 것을 떠올리고, 곰곰히 생각해보면 알수있다)
=> int형 배열을 5억짜리 크기로 만들어버리면 틀린 풀이가 된다.

기대된당~