System Optimization 기법

해킹(바이러스) 를 피하는 방법1 - 개발자가 해야할일

1. stack 의 사이즈를 충분히 넉넉하게 할당해서, buffer overflow 가 발생하는 일을 피하자.

2. gets(), strcpy() 등으로 입력받는 일을 피하자.
   => fegts(), strncpy() 등을 대신 사용하자!

fgets 는 정확하게 사용자에게 얼마만큼의 입력개수를 받아올것인지 명시적으로 선언해줘야한다.
ex) fgets(array, 4, stdin); // 명시적으로 최대 4개의 입력을 받아오겠다고 선언

---

해킹 피하는 방법2 - 시스템도 자동적으로 도와줌

1.Randomized stack offsets

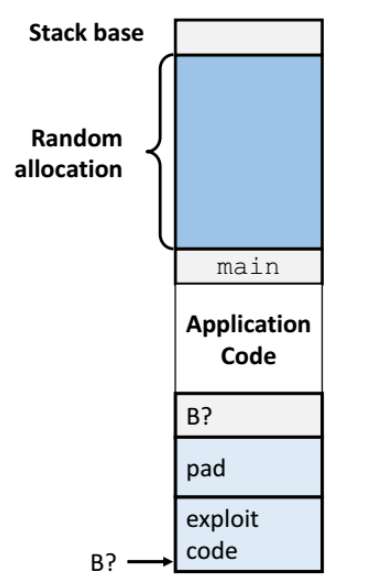
• 새로운 함수가 호출되었을 떄 stack frame 을 만들텐데, 이떄 스택의 return address 앞에다가 랜덤하게 빈칸을 준다.

• 해킹을 하려면 해당 stack frame 의 return address 까지의 정확한 사이즈를 파악해야 가능한데, 랜덤하게 빈칸을 부여하면 사이즈를 알 수 없으므로 해킹이 어려워진다.

  ---

2.exploit code(악성코드) 에 대한 실행 권한(executable) 없애기

(exploit code == 악성코드 부분)

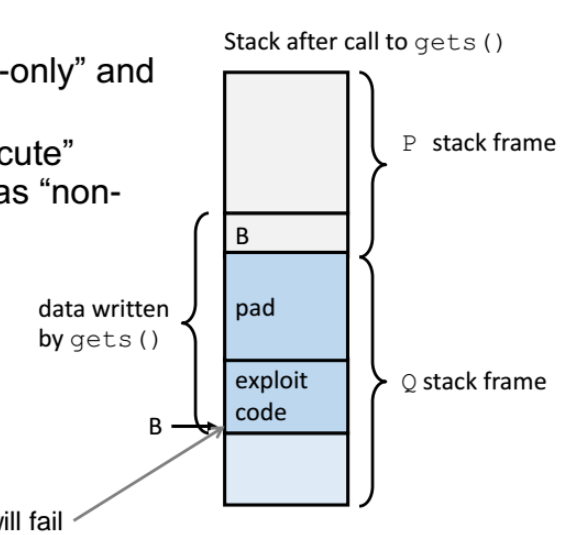
stack frame 의 top 에서 오버플로우가 발생되고 그 return address 를 오버라이트 할텐데, return address 가 스택에 있는 exploit code 로 갈것이다.

근데 이 소스코드에 대해 read, write, execute 권한이 있을텐데 이 중에 execute 권한을 빼버린다.

실행 권한이 없어서 실행못하고 에러 리턴하고 끝나버림!

---

3. 컴파일러도 알아서 "stack canaries" 라는 것을 추가할 수 있도록 도와준다.

stack frame 의 return address 바로 앞 공간에 canary 라는 난수를 넣어놓고, 오버플로우가 발생했을 때 canary 값을 바꾸었는지 안바꾸었는지를 판단하고, canary 값이 바뀌었다면 함수 리턴시 에러를 리턴하고 종료시키는 방법.
=> 즉, return address 를 건들이지 않도록 하기위한 용도

• GCC 의 경우 "-fstack-protector" 이라는 옵션을 주면 된다. (몰론 자동으로 들어가고 실행됨 )

• 컴파일러가 컴파일할떄 프로그램 실행하다가 도중에 프로그램을 중단시키고 꺼버림.

• 스택의 특정 주소에 flag 같은 것을 넣어놓는 것이다.

%fs:0x28 == stack canary

mov %fs:0x28, %rax : 스택의 특정 주소에 canary 를 넣어놓는다.

xor %fs:0x28, %rax : xor 함수를 리턴하기전에 canary 를 읽어온다. 그래서 다르면 에러메시지를 출력하는 곳으로 점프한다.

즉, 랜덤으로 생성되는 특정값(canary)을 return address 근처에다가 넣어놓고, 함수를 리턴하기전에 canary 값이 바뀌었는지를 비교한다.

• 값이 바뀌었다면 return address 도 바뀌었다고 가정하고 에러 메시지를 출력하는 곳으로 점프를 뛰어서 에러를 출력하고 함수를 리턴하는 것이다.

---

canary 예제

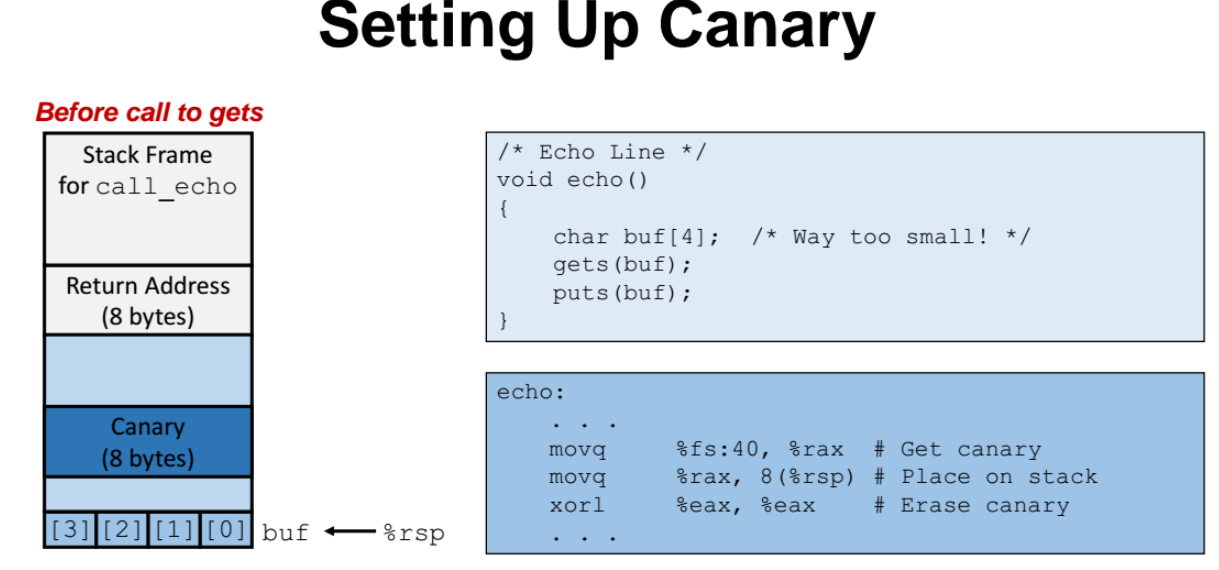
• return address 앞에다가 보듯이 8바이트짜리 난수(canary) 를 넣는다.

• char배열에 값을 넣다가 overflow 가 발생하면서 계속 위쪽에 값을 채워나갈텐데, 계속 채워나가다가 canary 를 마주쳤다면 canary 값을 바꿀 것이다.

• 코드 실행이 다 끝나고 함수를 리턴하기전에, 현재의 canary 값과 초기 기존의 canary 의 값을 비교해서 canary 값이 변했는지를 확인한다.

• canary 값이 변했다면, 함수를 리턴할때 에러를 리턴한다.

---

Return Oriented Programming Attacks

• 앞서 살펴본 code injection attack 을 다른말로 Return Oriented Programming Attacks 라고도 부른다.

=> return address 를 공략해서 내가 원하는 코드를 수행하는 것이 메커니즘이기 떄문이다.

• stdlib 라이브러리를 보면 해킹하기가 쉬워짐. 어느함수에 몇바이트에 있는지 등을 해커들이 쉽게 알 수 있다.

---

asymptotic complexity

• 프로그램은 기본적으로 알고리즘을 구현한것 (시간복잡도가 존재)
  • ex. 기본적으로 그림 띄우주는 프로그램도 알고리즘이 들어감

• constant factor 를 무시하면 성능이 느려진다!
  • constant factor 종류 : 알고리즘 시간복잡도, data representation, procedures, loops 등등

• 컴파일러는 프로그램을 바꿀 수 없다. 컴파일러는 c언어를 어셈블리로만 바꾸는 역할만 하면된다.

  • 몰론 컴파일러에게 OX3 이상의 옵션을 주면 살짝 바꾸긴함
  • 컴파일러가 최적화 과정은 기본적으로 한 함수 안에서만 수행한다.

---

일반적인 최적화

• Code Motion : 우리가 코드를 적을때 최적화 할수있는 방법을 잘 생각해보자!

아래처럼 배열같은 element 을 access 할때 인덱스를 계산하는데, n*i 를 반복문에서 매번 계산하는 것 보다 int ni = n x i; 처럼 반복문 밖으로 빼서 최적화를 시키자.

---

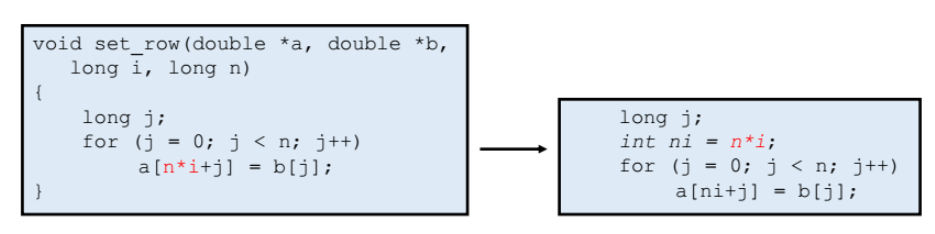
컴파일러의 최적화 (옵션 -O1)

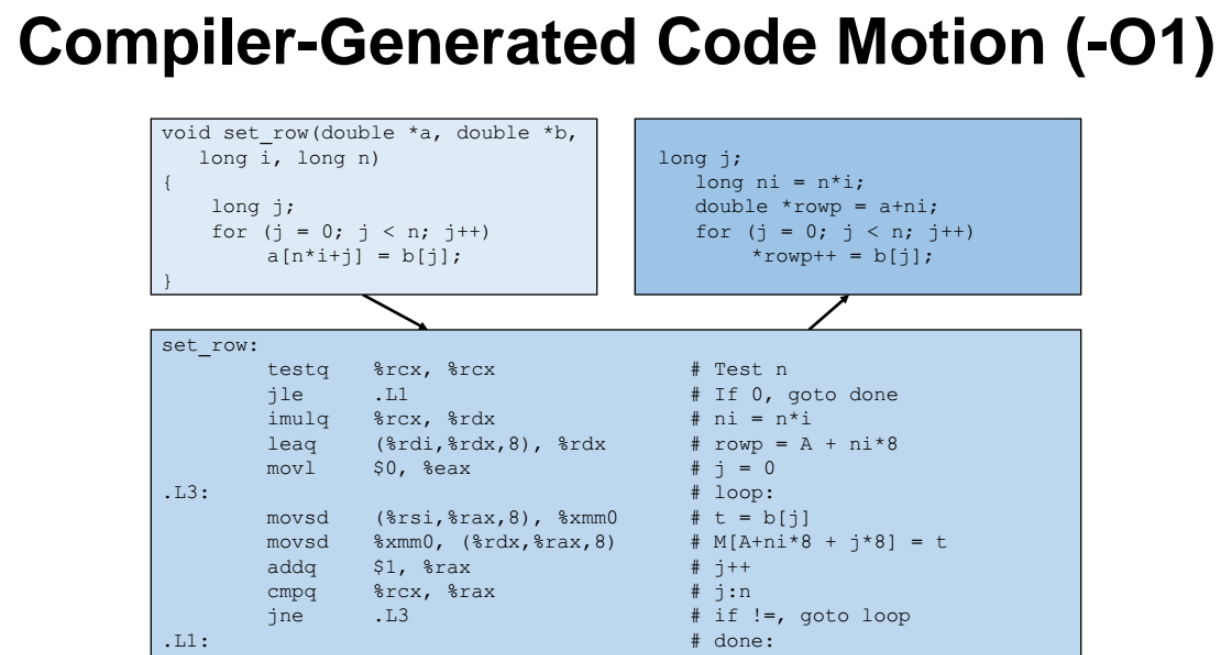
imulq %rcx, %rdx : 컴파일러가 알아서 n*i 값을 미리 loop (반복문)을 돌기전에 미리 계산하도록 최적화 과정을 마친다. 그리고 loop 를 돈다.

=> 이렇게 옵션 -O1을 부여서 컴파일러가 알아서 앞서 살펴본 code motion 을 해준다.

cf) %xmm0 : floating pointer number 로 중간범위 이후임

---

strength reduction

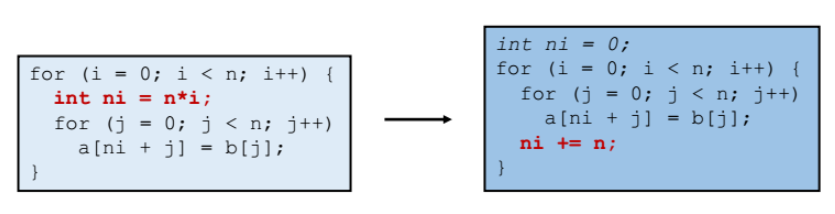
• 기본적으로 곱셈, 나눗셈 연산이 덧셈,뺄셈보다 CPU 사이클을 많이 사용한다.(성능 많이잡아먹음)

• 왼쪽의 곱하기 코드를 오른쪽처럼 더하기로 바꿨다. (prefix sum(누적합))
  이렇게 해야 성능더 좋아짐.

shift 연산

• shift 연산 : 곱하기, 나누기 연산 대신에 shift 연산을 사용하는게 좋다
  (특히 2의 배수에 대한 곱셈, 나눗셈 연산일 때 더더욱!)

=> ex) 16 * x => x << 4 로 대체하자. 16를 곱하느니, 차라리 비트를 4번 밀어버리자!

---

share common sub-expressions

왼쪽코드

• 아래 예제는 two-dimensional array (2차원 배열) 에서 좌표 (i,j) 의 상하좌우에 인접한 4개의 원소들의 값을 구해내고 sum 을 하는 것이다.

=> 컴파일된 결과인 어셈블리 코드를 보면 곱셈이 총 3번 일어난다.

오른쪽코드

• -O1 옵션을 부여한 경우로, 최적화가 된 경과이다.
• 곱셈이 1번으로 줄었다. i x n 값을 구하고 이 값을 계속해서 재활용하면 된다.

---

Optimization Blocker

• 최적화(Optimization) 를 못하게 하는 놈들

예제

위 lower 함수는 s[i] 가 대문자인지 아닌지를 판단하기 위해 A 와 Z 와 비교하는 연산을 수행한다. s[i] 가 대문자라면 'A'-'a' 값을 빼서, s[i] 라는 대문자를 소문자로 바꿔주는 함수이다.

=> 예는 loop (for문) 도 있어서 성능을 향상시키고 싶지만 못한다.

• s 를 보면서 최적화할 내용을 찾고싶을텐데, s는 함수의 파라미터로써 함수의 밖에서 받아온 것이다. 즉, s의 길이도 얼마인지 모르고, s 안에 예를들어 혹시 NUll pointer 가 들어가 있을지등의 특이사항이 있을지도 모르는 것이다.

  => 함수 밖에서 받아온 데이터에는 직접 손을 대지못한다(건들지못함ㅠㅠ)

• 앞서 설명했듯이, 컴파일러의 최적화 과정은 기본적으로 한 함수 안에서만 수행한다고 했었다. 이런 외부 변수는 어떻게 최적화 과정을 진행못함!

이렇게 최적화를 시키지 못하는 경우를 Optimization blocker 라고 한다.

---

strlen() 성능

• strlen() 은 문자열의 길이를 구하는 함수로써, 시간복잡도는 O(n) 이다.
  이때 아래처럼 for문안에 strlen() 을 넣어둔다면 매번 strlen 함수의 호출이 일어나서 O(n^2) 이기 때문에 비효율적이다.

아래처럼 code motion 을 통해 우리가 코드를 바꿔주면 성능 최적화 쌉가능. 이렇게 코드 바꿔주면 컴파일러가 알아서 내부적으로 최적화해줌.

또는 인라인 함수를 사용하면, 어셈블리 코드가 짧을경우 jump 과정이 생략되어서 성능이 좋아진다.

---

Memory Aliasing

• 마찬가지로 최적화 못하게 함

• a와 b는 함수 밖에서 받아온 인풋이다.

• memory aliasing : 이때 a, b 는 포인터로써 어떤 메모리의 주소를 각자 가리키고 있을텐데, 만일 a, b 외에 c라는 다른 포인터가 같은 메모리 공간을 가리키고 있을때 이를 memory aliasing 이라고 한다.

• 위 코드를 보면 b[i] == a[i*n + j]; 에서 b[i] 에다 a를 더하고있다. 그런데 double B[3] = A + 3; 과 같이 B가 배열 A의 중간 어딘가 부분을 가리키고 있었다고 하자. 이게 memory aliasing 이다. A는 크기가 9인 메모리 공간을 가리키고 있을텐데, B가 A의 한 가운데인 {4,8,16} 쪽을 가리키고 있다.

=> 그러면 b[i] = a[i*n + 3]; 연산을 다시 보면 b에다 a를 더하고 있다. 이러면 B의 값이 바뀔떄 A의 값도 바뀐다.

=> 이는 물리적으로 말이 안되고 허용되지 않는다. 이러한 memory aliasing 은 컴파일러에서 수행하지 않는다.

이런 memory aliasing 대신에 val += a[i*n +j]; 처럼 val 지역변수를 만들고 거기에 a[i*n +j] 값을 더하고, b[i] 에다 val 를 할당하는 안전한 방법을 선택하자!

---

Exploiting Instruction - Level Parallelism

• CPU에는 코어가 여럿 들어있는데, 코어는 instruction(명령)을 한번에 여러개 수행한다.

ex) add 명령어
1.명령이 add 인것을 인지하기 위해, 명령을 메모리에서 CPU에게 갖다준다.

2.add 에 대한 명령과 함께 src(source)와 dst(destination) 이 전달될텐데, 해당 src dst 으로부터 데이터를 추출해온다.

3.실제로 더하기 계산을 진행한다.

4.retq 로 리턴한다.

=> 이렇듯 각 스탭이 순차적으로 수행될것같지만, 각 스탭은 dependency(의존성) 없이 독립적으로 수행된다.
(쉽게말해, 각 스탭은 순차적으로 수행하는 것이 아닌 일정량을 동시에 수행한다.)

---

Benchmark

Benchmark : 우리가 어떤 특정 기능의 성능을 알고싶을때, 그 기능에 대해 계속 스트래스를 주입해서 성능을 파악하는 것이다.

예를들어 우리가 메모리를 얼마나 사용하는지 관심이있다면, 메모리를 많이 할당받고 자주 사용하고 free 하는등을 하는 소프트웨어이다.

Benchmark 소프트웨어로 프로그램을 실행시키면 성능이 나올것이다. 그것을 가지고 다른 성능들과 비교를 하는 것이다.

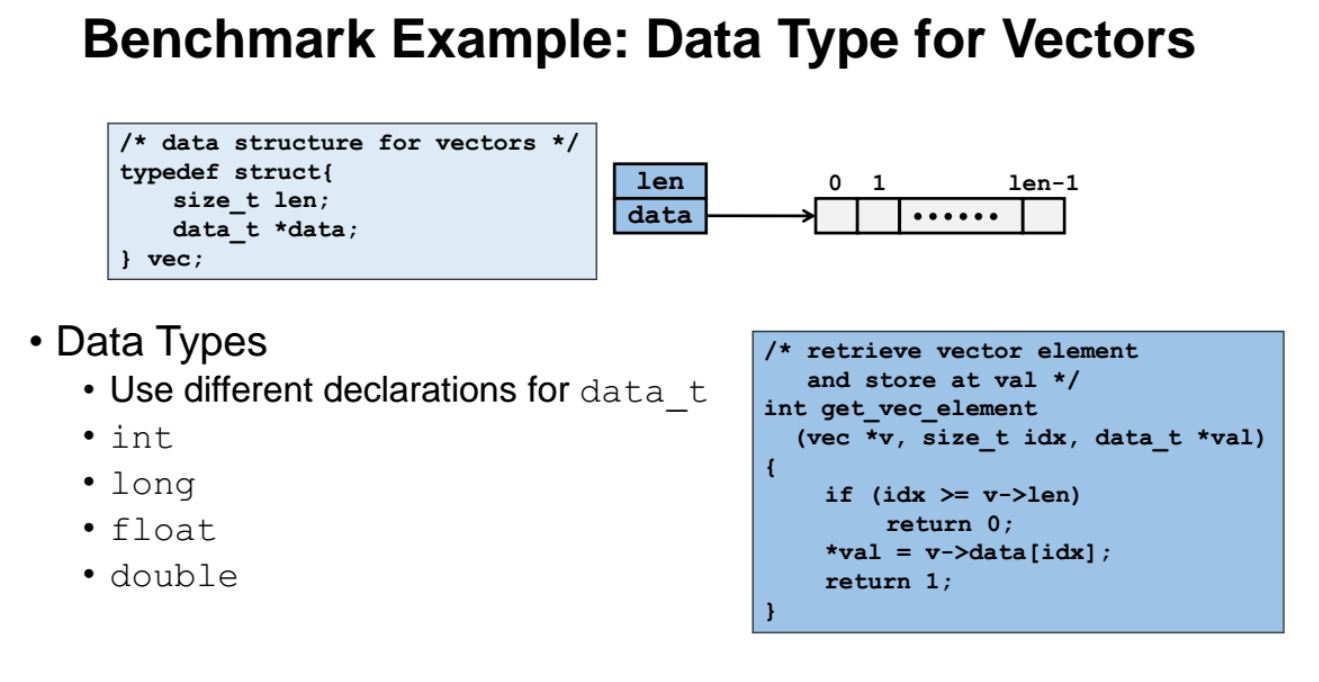
• get_vec_element 함수는 idx 인덱스에 들어있는 값을 얻어와서, val 포인터가 가리키고 있는 메모리에 저장하는 함수이다.

• "data_t" 에 int, long, float, double 등의 어떤 데이터 타입을 할 당하는가에 따른 성능을 분석하는 benchmark 이다.

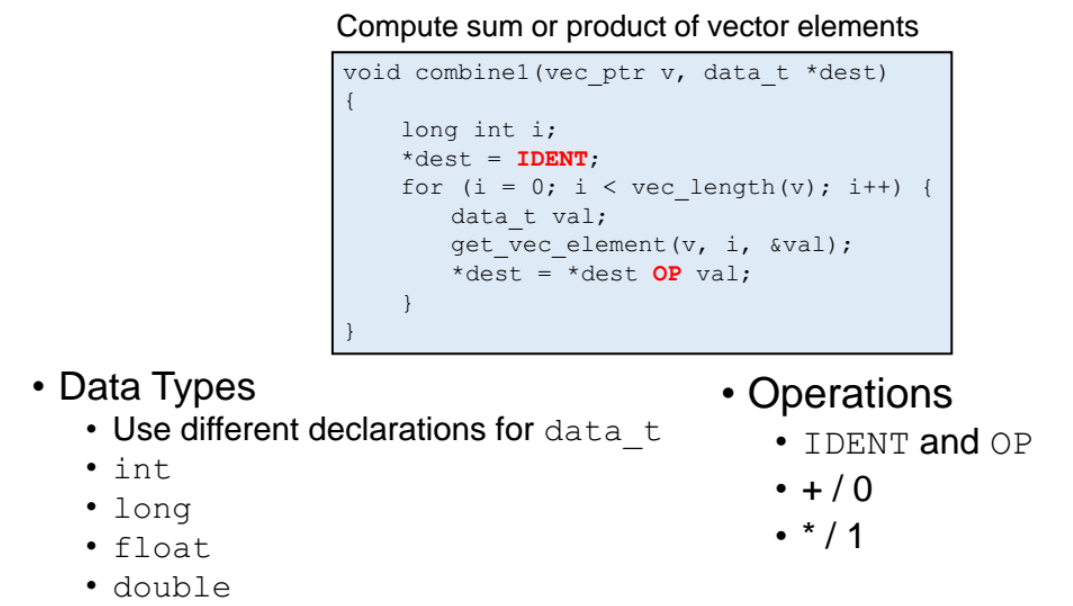
• base line : benchmark 로 성능을 분석시, 성능을 분석하기 위한 기준

• 벡터 v 의 length 만큼 for문을 돌면서 벡터의 각 원소의 값을 가져와서 현재 리턴할 값에다가 덧셈 또는 곱셈을 해준다. 초기값이 0이면 덧셈을 하고, 1이면 곱셉을 한다. (=> 즉 벡터의 원소들을 다 더하거나 곱해준다!)

=> 이러한 벡터 연산을 진행할때 벡터의 타입을 int, long, float, double 등의 다양한 타입에 따른 연산 성능을 분석하는 benchmark 소프트웨어이다.

Cycles Per Element (CPE)

• 앞선 코드를 컴파일하기전에, CPE matrix 를 사용한다.
  이는 CPU Cycle 을 사용하는 얼마나 되는지를 보는 것이다.

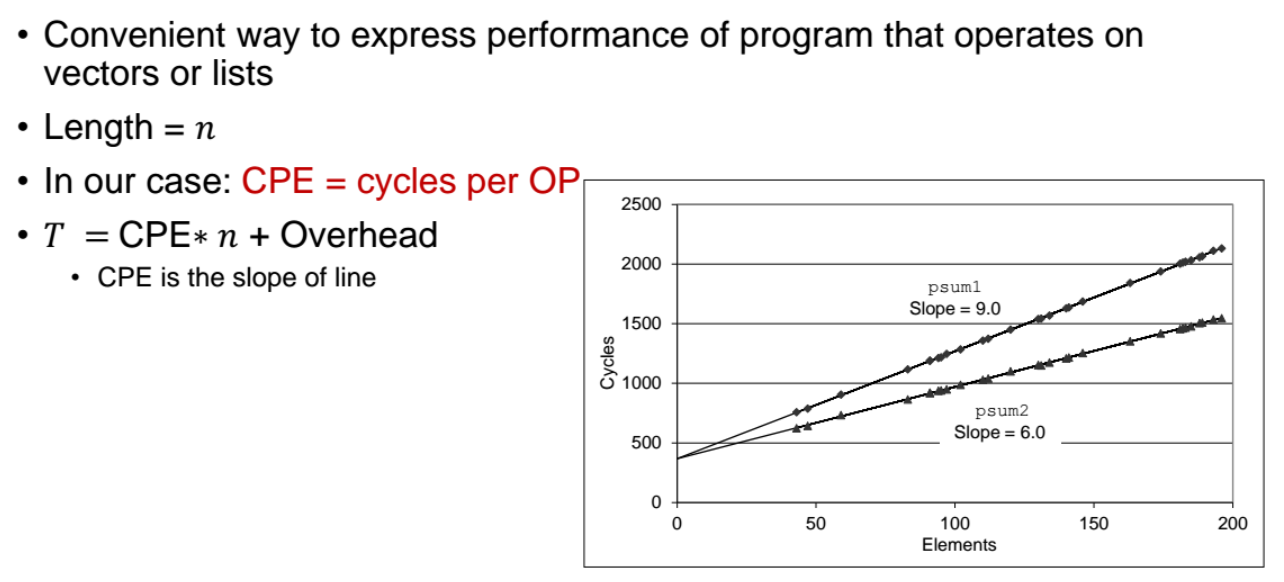
= n=벡터의길이, CPE = cycle per element = 인풋 element 개수

• 위 그래프처럼 CPE (인풋 element 개수) 가 많아질수록 걸리는 시간(=cycle) 이 커질텐데, slope 가 낮아질수록 직선의 기울기가 낮아서 성능이 더 좋은것이다. 0

---

• 위 표는 컴파일 결과로써 integer를 부여했을때의 덧셈과 곱셈의 수행시간, double 을 부여했을떄의 덧셈과 곱셈의 수행시간을 나타낸것이다.

• -O1 옵션을 부여해서 컴파일했을때 최적화의 결과는 옵션을 부여안했을떄에 비해서 대략 2배나 빨라졌다.

컴파일러가 어떻게 했길래 2배나 빨라졌을까?
=> 앞서 살펴본 block code 들이 없다. 즉, code motion, struct reduction 등 할수있는일은 다 했을 것이다.

---

그런데 컴파일 결과, 즉 최적화가 이게 최선일까? 아니다.

일단, length 를 loop 밖에서 받도록 하는 code motion 을 컴파일러에서 진행했다. 여기서 그치지 않고 우리가 직접 code motion 을 해서 성능을 더 개선시킬 수 있다.

---

그런데 우리가 직접 code motion 을 하면서 코드를 개선했을 떄 성능이 -O1 을 부여했을떄 보다 성능이 굉장히 위처럼 좋아질 수 있다.

=> 즉, 옵션 -01 으로 컴파일러를 통해 코드를 수정하고, 그 코드를 우리가 code motion 을 통해 코드를 또 수정하면 성능이 대폭 향상되었음을 알 수 있다.

그런데 여기서 또 성능을 좋게 만들수있다. 방금전까지 한 과정들은 우리가 배운 내용들로 최적화를 한것인데, 앞으로의 내용을 활용하면 성능이 훨씬 좋아진다.

---

---

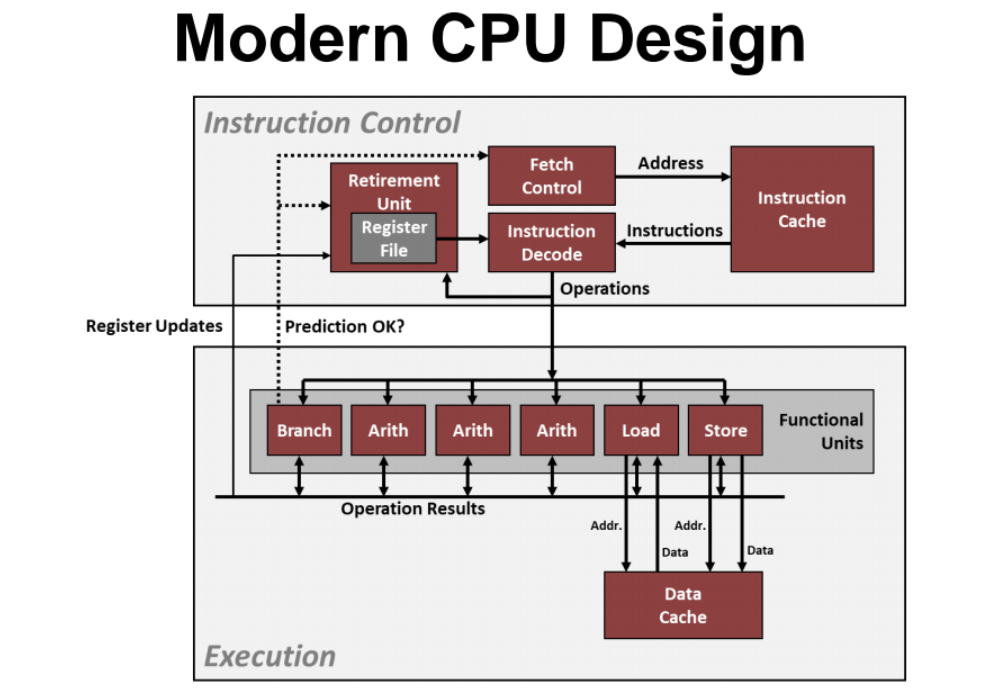
Superscalar Processor

• 여러 명령들을 동시에 수행시킬수 있는 CPU의 코어들
  (can execute multiple instructions in one cycle)

Bubble 발생 - 동시에 여러 명령들을 실행못시키는 경우

=> ex) x=1; y=x; 코드가 있을때 : x=1; 명령에 대한 수행이 끝나기전까지 y=x; 명령을 수행하지 못한다.

• 이런 경우에 데이터간의 dependency 가 생겼다고 하며, Bubble 이 생겼다고 한다. ( 이런 코드가 instruction Parallelism 활용하지 못하는 안좋은 코드이다 )

---

• p3 = p1 p2; 연산은 p1=ab; p2=a*c; 명령이 수행완료 되기 전까지 수행하지 못한다.

• time 라인을 보면 스탭 3과 4에 빈칸이 6개나 있다. 이 빈칸을 instruction parallelism 을 활용해서 적절히 제거해줘야한다.

---

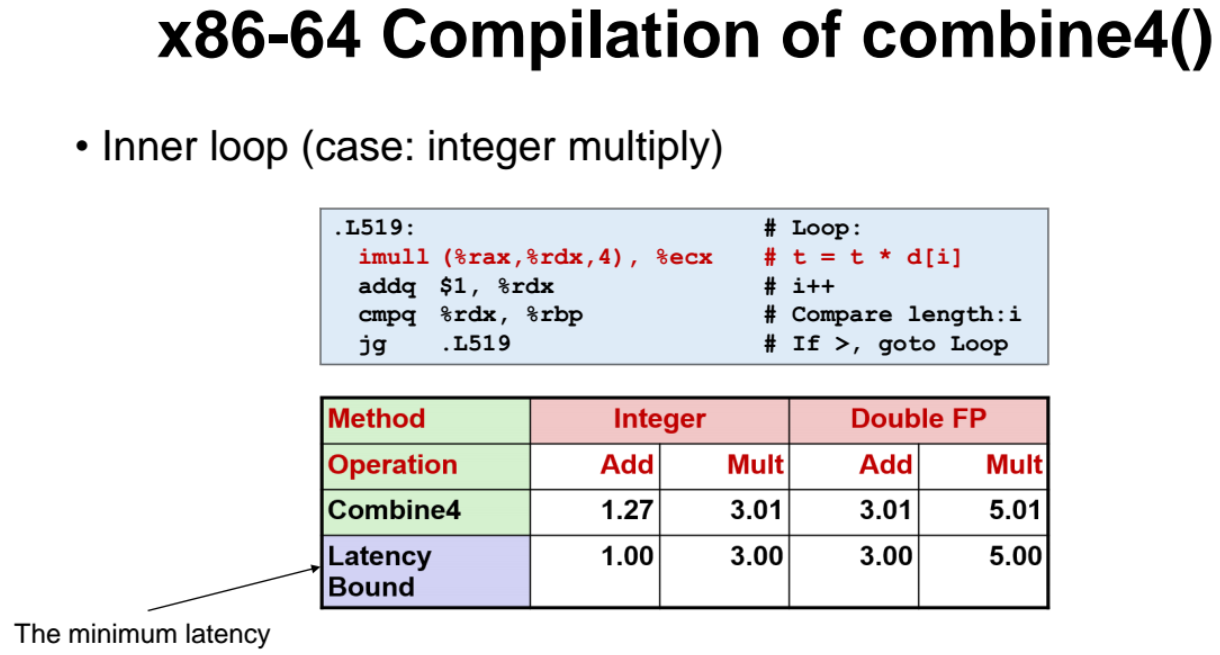
• latency bound : 최소 처리 지연시간 (처리하는데 걸리는 시간)
  • 연산 속도가 상황에 따라 다를텐데, 아무리 빨라도 latency bound 시간보다 빠를수가없다. (즉, latency bound 란 명령을 처리하는데 걸리는 가장 빠른시간)

보듯이 integer 가 연산이 개빠르다.

---

아까 살펴본 함수 예제를 다시 살펴보자.
각 연산을 진행했을 때 추출된 t 값이 다른 스탭의 연산의 t 값과 dependent 하다.

한 스탭의 연산 수행결과 t가 다음 연산의 수행결과에 영향을 미치므로 dependent 한것이고, 명령들이 동시에 수행되지 못하고 순차적으로 수행되어야한다. (sequential dependence)

• 만일 중간에 이 seqence 를 break 하면 결과값이 바뀌게된다.
  그래서 이를 해결하기 위한 방안이 2가지가 있다.

Loop Unrolloing

• 앞선 combine4 코드를 조금 수정한 함수이다. combine4 함수는 인덱스 i값을 1씩 증가시켰지만 d[i] 값을 계속 누적시켰지만, 여기서는 인덱스 i값을 2씩 증가시키면서 d[i] + d[i+i] 의 값을 더하면서 값을 계속 누적시키는 방식이다.

=> 이에따라 OP 연산도 for 문의 루프를 1번돌때 2번 수행하는 것이다.

=> 이렇게 기존에 rolled 되어있던 루프를 한번에 unroll 해서 루프를 도는것을 loop unrolling 이라한다.

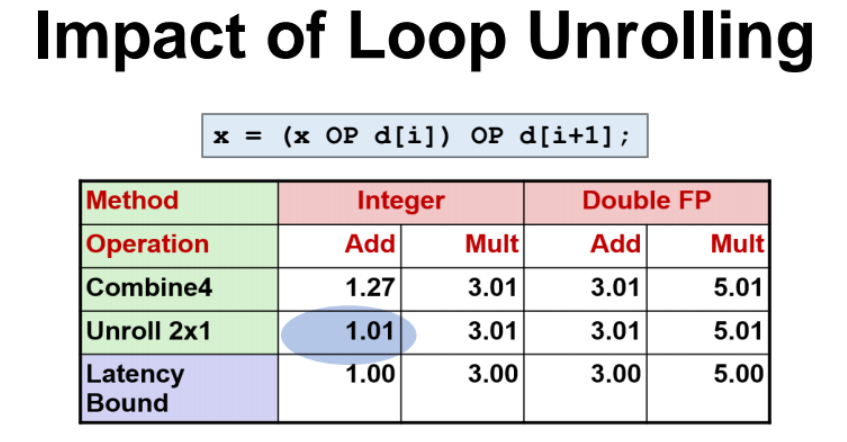
성능을 확인해보면 엄청 좋아짐!

Loop Unrolling with Re-association

• 루프안에서 OP 연산의 순서를 바꾸면 아래와 성능이 더 향상될 수 있다.

위처럼 하면 하나하나 따로 진행했던 연산이 동시에 진행되서 연산이 더 빨라진것이다. 개쩐다 latency bound 보다 성능이 더 빠르다니!

연산 구조

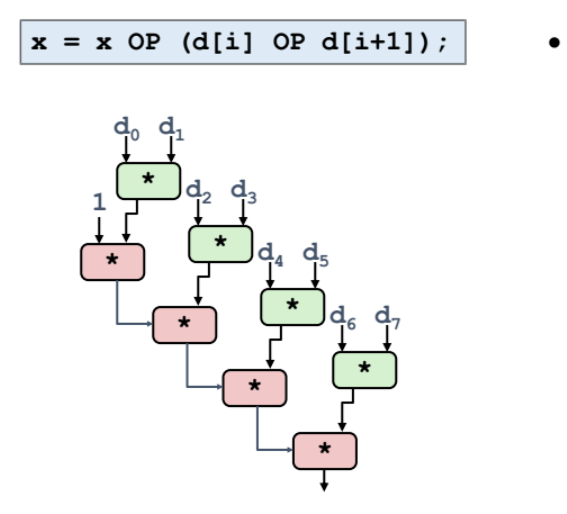
위 그림처럼, d[i] 와 d[i+1] 를 OP 하는 연산을 동시에 진행 가능하게 되었다.

아까 코드에 비해 현재 코드는 dependency 가 없어져서 동시에 진행 가능한것.

---

Loop unrolling 을 2번에 나눠서 진행하기

• Loop unrolling 을 2번에 나눠서 진행하면 성능이 또 향상된다니..!
  지역변수 x0, x1 을 만들고 OP 연산을 따로 진행하니 dependency 가 없어져서 연산을 동시에 수행가능.
  덧셈 수행시간 빨라짐!

---

Unrolling and Accumlating 특징 정리

• 지금껏 살펴봤듯이, 수식연산(arithmetic operation) 은 동시에 최대 4개를 수행 가능하다.

• 위에서 루프에 unroll 을 2번 넣어줬었는데, 만일 4번을 넘는다면 동시 수행이 불가능함

---